工程力学-动力学/Technische Mechanik IV – Dynamik - Integration der Eulerschen Gleichungen 欧拉方程的积分

2023-06-13 | 阅读：次

Integration der Eulerschen Gleichungen 欧拉方程的积分

EULERSCHE Kreiselgleichungen 欧拉陀螺仪方程

Eulersche Gleichungen beschreiben allgemeine Bewegung eines starren Körpers mit einem fixen Punkt.欧拉方程描述了具有固定点的刚体的一般运动。

\[\begin{aligned} & \dot{\omega}_1 J_{11}-\omega_2 \omega_3\left(J_{22}-J_{33}\right)=M_1 \\ & \dot{\omega}_2 J_{22}-\omega_3 \omega_1\left(J_{33}-J_{11}\right)=M_2 \\ & \dot{\omega}_3 J_{33}-\omega_2 \omega_1\left(J_{11}-J_{22}\right)=M_3 \end{aligned}\]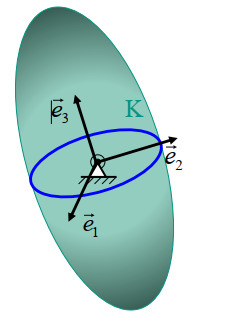

Das Problem der analytischen Lösung dieser Gleichungen hat Wissenschaftler weit über 100 Jahre intensiv beschäftigt. Am Ende hat sich herausgestellt, dass es nur drei Fälle gibt, in denen diese Gleichungen vollständig lösbar sind. (Natürlich numerische Näherungslösung ist immer möglich). Die Nichtintegrierbarkeit dieser Gleichungen wurde ähnlich wir beim Dreikörperproblem auf die fundamentale Arbeiten vom französischen Mathematiker Henry Poincare Ende des XIX Jahrhundert zurückgeführt. Die drei Fälle der Integrierbarkeit werden nach ihren Erfinder genannt

100 多年来，这些方程的解析解问题一直困扰着科学家们。最后发现只有三种情况可以完全求解这些方程。（当然，数值近似总是可能的）。与三体问题类似，这些方程的不可积性问题可以追溯到19世纪末法国数学家亨利庞加莱的基础工作。可积性的三种情况以其发明者的名字命名

Der einfachste Falls wurde von Euler untersucht und beschäftigt sich mit einem Körper in der Situation, wo das resultierende Moment aller äußerer Kräfte verschwindet (gleich null ist). Dieser Fall wird realisiert, wenn ein schwerer Kreisel sich im homogenen Schwerekraft (z.B. der Erde befindet) und in seinem Schwerpunkt fixiert wird, d.h. der Aufhänge punkt befindet sich im Schwerpunkt des Körpers. In diesem Fall vereinfachen sich die Bewegungsgleichungen:

Kräftefreier Kreisel (Der Eulersche Fall) 陀螺仪

这种最简单的情况是由欧拉研究的，涉及到一个物体在所有外力产生的力矩之和为零的情况。这种情况在一个重质量陀螺仪位于均匀重力场（例如地球）并且被固定在其质心的情况下实现，也就是悬挂点位于物体的质心。在这种情况下，运动方程变得更简化：

Zunächst wird der einfachste Fall eines symmetrischen Körpers behandelt. In diesem Fall können die Gleichungen in elementaren Funktionen integriert werden:

首先，处理对称体的最简单情况。在这种情况下，方程可以集成为初等函数：

\[\begin{aligned} & J_{11}=J_{22}=A ; \quad J_{33}=C \\ & \dot{\omega}_1 A+\omega_2 \omega_3(C-A)=0 \\ & \dot{\omega}_2 A-\omega_3 \omega_1(C-A)=0 \\ & \dot{\omega}_3 C=0 \end{aligned}\]

Kräftefreier symmetrischer Kreisel. Kinetik 没有外力作用、具有对称性的陀螺

\[\begin{aligned} & \dot{\omega}_1 A+\omega_2 \omega_3(C-A)=0 \\ & \dot{\omega}_2 A-\omega_3 \omega_1(C-A)=0 \\ & \dot{\omega}_3 C=0 \quad \dot{\omega}_3=0 \rightarrow \quad \omega_3=\omega_{30}=\text { konst } \\ & \left\{\begin{array}{l} \dot{\omega}_1+\omega_2 \omega_{30} \frac{C-A}{A}=0 \\ \dot{\omega}_2-\omega_1 \omega_{30} \frac{C-A}{A}=0 \end{array} \rightarrow \quad \ddot{\omega}_2=\dot{\omega}_1 \omega_{30} \frac{C-A}{A}=-\omega_1\left(\omega_{30} \frac{C-A}{A}\right)^2\right. \\ & \ddot{\omega}_2+\left(\omega_{30} \frac{C-A}{A}\right)^2 \omega_2=0 \quad \rightarrow \quad \omega_2=\omega_0 \sin \left(\omega_{30} \frac{C-A}{A} t+\alpha_0\right) \\ & \omega_1=\frac{A}{C-A} \frac{1}{\omega_{30}} \dot{\omega}_2=\frac{A}{C-A} \frac{1}{\omega_{30}} \omega_0 \omega_{30} \frac{C-A}{A} \cos \left(\omega_{30} \frac{C-A}{A} t+\alpha_0\right) \\ & \omega_1=\omega_0 \cos \left(\omega_{30} \frac{C-A}{A} t+\alpha_0\right) \\ & \end{aligned}\]

Damit sind die Komponenten der Winkelgeschwindigkeit vollständig bestimmt. Es bleiben die kinematischen Gleichungen zur Bestimmung der Eulerschen Winkel als Funktionen der Zeit.
角速度的分量因此被完全确定。用于确定作为时间函数的欧拉角的运动学方程仍然存在。

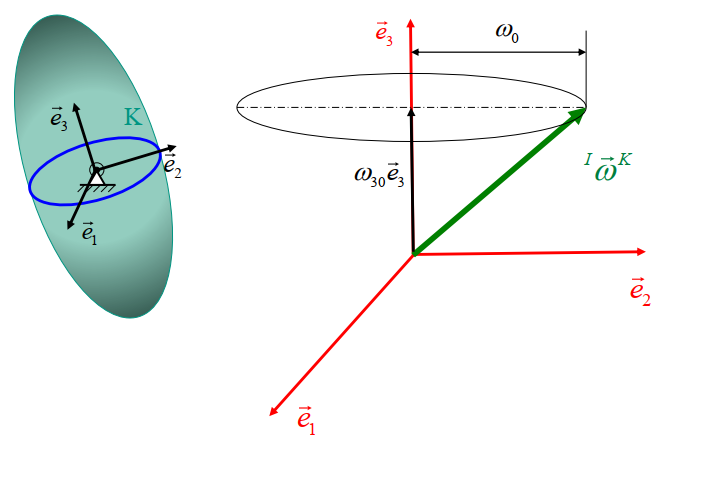
Geometrische Interpretation: Innerhalb des Körpers umläuft der Vektor der Winkelgeschwindigkeit einen Kreis. Die Umlaufgeschwindigkeit hängt von den Anfangsbedingungen und der Verhältnis der Massenträgheits-momente des Körpers ab.
几何解释：在物体内部，角速度的矢量绕着一个圆旋转。旋转速度取决于初始条件和物体的转动惯量之比。

\[\Omega_{\text {Umlauf }}=\omega_{30} \frac{C-A}{A}\]

Ermittlung kinematischer Größen wird möglich, wenn wir beachten, dass die Zeitableitung des Drehmomentes im raumfesten Bezugssystem in Abwesenheit des äußeren Momentes gleich null ist.
当我们注意到在没有外部力矩的情况下，相对于固定空间参考系的力矩的时间导数为零时，我们就可以确定运动学量。

“kinematische Größen” 指的是描述物体运动的量，而不考虑所受到的力或力矩的影响。它们通常包括位置、速度、加速度和角度等物理量。运动学是研究物体运动的分支，主要关注物体的运动状态和其随时间的变化，而不涉及导致这些变化的具体力量或力矩。因此，kinematische Größen 是用来描述物体运动的量，从而提供关于物体位置、速度和加速度等方面的信息。

\[\frac{ {\quad}^I d \vec{L}^{(s)}}{d t}=\overrightarrow{0} \quad \rightarrow \quad \vec{L}^{(s)}=\text { konst }\]

Dies bedeutet, dass der Drall-Vektor in seiner Richtung und betrag konstant bleibt. Wählen wir die raumfesten Koordinaten so, dass der Basisvektor entlang des Drall i3 -Vektors gerichtet ist:
这意味着扭曲矢量的方向和大小保持不变。让我们选择空间固定坐标，使基本向量沿着扭曲 i3 向量定向：

\[\vec{L}^{(S)}=L\vec{i}_{\text{3}}\]

Anderseits gilt (vgl. Vorlesung 2, Folie 10): 另一方面（参见第 2 讲，幻灯片 10）：

\[\vec{L}^{(S)}=\vec{\vec{J}}^{(S)}\cdot{}^I\vec{\omega}^K=A\omega_1\vec{e}_1+A\omega_2\vec{e}_2+C\omega_3\vec{e}_3\]

Aus der Definition der Euler-Winkeln folgt dann:
根据欧拉角的定义，可以得出：

\[\begin{aligned} &C\omega_3=L\cos\theta \\ &A\omega_1 =L\sin\theta\sin\varphi \\ &A\omega_2 =L\sin\theta\cos\varphi \end{aligned}\]

Hinweis: Drehung um $\psi$ verändert den Drall-Vektor nicht.
注意：关于$\psi$的旋转不会改变扭曲向量。

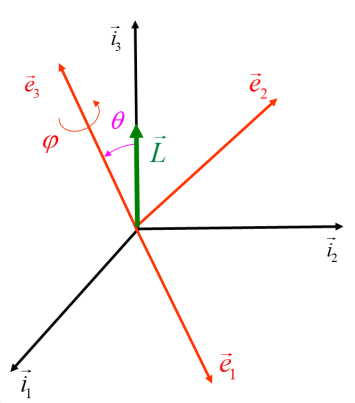
Daraus folgt sofort:

\[\begin{aligned} & C \omega_3=L \cos \theta \rightarrow \quad \cos \theta=\frac{C \omega_3}{L}=\frac{C \omega_{30}}{L}=\text { konst } \\ & \theta=\theta_0=\arccos \left(\frac{C \omega_{30}}{L}\right) \\ & \left.\begin{array}{l} A \omega_1=L \sin \theta \sin \varphi \\ A \omega_2=L \sin \theta \cos \varphi \end{array}\right\} \\ & \rightarrow \tan \varphi=\frac{\omega_1}{\omega_2}=\frac{\cos \left(\omega_{30} \frac{C-A}{A} t+\alpha_0\right)}{\sin \left(\omega_{30} \frac{C-A}{A} t+\alpha_0\right)}=\cot \left(\omega_{30} \frac{C-A}{A} t+\alpha_0\right) \\ & \varphi=\frac{\pi}{2}-\omega_{30} \frac{C-A}{A} t+\alpha_0 ; \quad \dot{\varphi}=-\omega_{30} \frac{C-A}{A}=\text { konst } \\ & \dot{\psi} \cos \theta+\dot{\varphi}=\omega_{30} \quad \rightarrow \quad \dot{\psi} \frac{C \omega_{30}}{L}-\omega_{30} \frac{C-A}{A}=\omega_{30} \\ & \dot{\psi} \frac{C}{L}-\frac{C-A}{A}=1 \quad \rightarrow \quad \dot{\psi}=\frac{L}{A}=\text { konst } \\ & \end{aligned}\]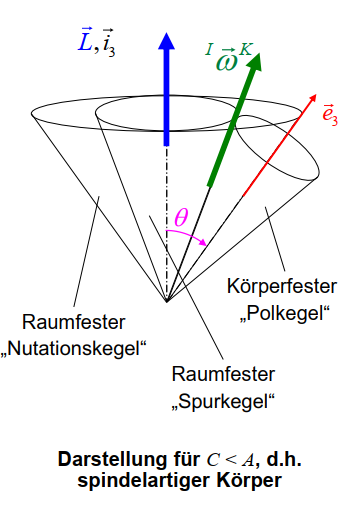

在刚体动力学中，”Nutationskegel” 是指在陀螺体或旋转物体的运动中，其自旋轴相对于固定空间的进动轴所形成的圆锥。这个圆锥的顶点位于陀螺体的自旋轴上，而圆锥的轴线则与进动轴重合。由于陀螺体的自旋轴会绕着进动轴进行进动，所以形成了这个进动圆锥。

“Raumfester” 意味着这个进动圆锥是相对于固定的空间来定义和测量的，而不是相对于陀螺体自身。这意味着进动圆锥的方向和位置在固定空间中保持不变，不受陀螺体自身旋转的影响。

因此，”Raumfester Nutationskegel” 指的是固定在空间中的进动圆锥，用于描述陀螺体或旋转物体的运动特性。

在刚体动力学中，”Spurkegel” 是指在陀螺体或旋转物体的运动中，其迹点（运动轨迹上的点）相对于固定空间的运动形成的圆锥。这个圆锥的顶点位于迹点所在的位置，而圆锥的轴线则与迹点在空间中的运动方向相对应。

“Raumfester” 表示这个迹圆锥是相对于固定的空间来定义和测量的，而不是相对于陀螺体自身。这意味着迹圆锥的方向和位置在固定空间中保持不变，不受陀螺体自身旋转的影响。

因此，”Raumfester Spurkegel” 指的是固定在空间中的迹圆锥，用于描述陀螺体或旋转物体迹点的运动特性。

在刚体动力学中，”Polkegel” 是指在陀螺体或旋转物体的运动中，其极轴所形成的圆锥。这个圆锥的顶点位于极轴所在的位置，而圆锥的轴线则与极轴重合。

“Körperfester” 表示这个极锥是相对于陀螺体自身来定义和测量的，而不是相对于外部空间。这意味着极锥的方向和位置随着陀螺体的运动而变化，取决于陀螺体自身的姿态和旋转状态。

因此，”Körperfester Polkegel” 指的是固定在陀螺体自身的极锥，用于描述陀螺体的旋转特性和姿态。

Geometrische Interpretation 几何解释

Der Körper dreht sich mit konstanter Geschwindigkeit $\dot{\varphi}$ um seine Hauptachse $\overrightarrow{e_{3}}$.

Diese Achse selbst dreht sich mit konstanter Geschwindigkeit $\vec{i}_3$ um die raumfeste Achse, d.h. um den Drall-Vektor $\dot{\psi}$.

Diese Bewegung wird als reguläre freie Präzession bezeichnet.

物体以恒定速度 $\dot{\varphi}$ 绕其主轴 $\overrightarrow{e_{3}}$ 自转。

这个轴本身以恒定速度 $\vec{i}_3$ 绕固定轴旋转，即绕着进动矢量 $\dot{\psi}$。

这种运动被称为规则的自由进动。

\[\left.\begin{array}{l} \dot{\psi}=\frac{L}{A} \\ \cos \theta=\frac{C \omega_{30}}{L} \\ \dot{\varphi}=-\omega_{30} \frac{C-A}{A} \end{array}\right\}\] \[\begin{gathered} L=A \dot{\psi} \\ \rightarrow \quad \omega_{30}=\frac{L}{C} \cos \theta=\frac{A}{C} \dot{\psi} \cos \theta \\ \dot{\varphi}+\frac{C-A}{A} \dot{\psi} \cos \theta=0 \end{gathered}\]

Die letzte Gleichung enthält keine Anfangsbedingungen und stellt den kinematischen Zusammenhang (vgl. Kepplersche Gesetze) dar.
Die Bewegung kann wie Abrollen des körperfesten Polkegels (von außen) auf dem raumfesten Spurkegel interpretiert werden. Punkte des Körpers bewegen sich auf Epizykloiden

最后一个方程不包含任何初始条件并表示运动学关系（参见开普勒定律）。
该运动可以解释为固定体极锥（从外部）在固定空间轨道锥上的滚动。物体的点在外摆线上移动

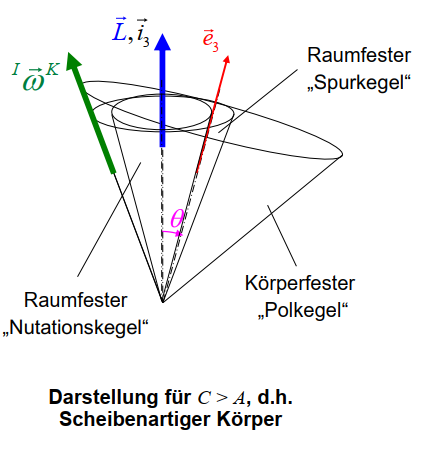
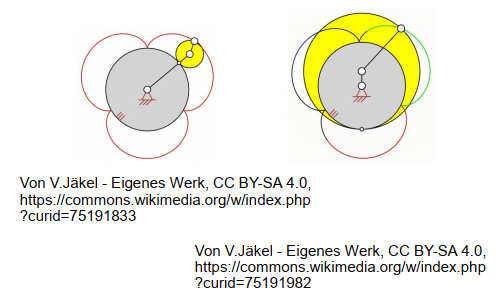
Auch hier kann die Bewegung wie Abrollen des körperfesten Polkegels (von innen) auf dem raumfesten Spurkegels interpretiert werden. Punkte des Körpers bewegen sich auf Perizykloiden
这里的运动也可以解释为刚体固定的极锥（从内部）在固定的迹锥上滚动。物体上的点沿着柏拉克罗侧线运动。

这句话描述了一种运动的解释，其中涉及到刚体固定的极锥和固定的迹锥之间的关系。具体而言，它提到了刚体固定的极锥从内部滚动在固定的迹锥上的过程。在这个过程中，物体上的点按照柏拉克罗侧线的路径进行运动。

“Perizykloiden”（柏拉克罗侧线）是一个几何学术语，指的是由一个固定圆与一个在其上滚动的小圆所形成的曲线。在这种描述中，物体上的点运动的路径类似于柏拉克罗侧线。

Kräftefreier unsymmetrischer Kreisel.非对称陀螺仪。

Der Fall von Euler - Poinsot

Euler-Poinsot陀螺，也称为Euler-Poinsot陀螺体或Euler陀螺，是一种具有特殊运动特性的刚体模型，它展示了一种被称为Euler-Poinsot情形的旋转现象。

在Euler-Poinsot情形下，刚体围绕其一个主惯性轴（也称为长轴）旋转，同时绕另外两个互相垂直的瞬时旋转轴（也称为短轴）进行进动。这种运动形式是非常特殊和复杂的，因为它涉及到刚体的自旋和进动的相互耦合。

Euler-Poinsot陀螺的运动过程中，其自旋和进动的角速度以及角动量都会发生变化。这种陀螺的稳定性和运动特性使其成为研究刚体动力学和旋转物体行为的重要示例。

Euler-Poinsot情形得名于法国数学家与物理学家Leonhard Euler和Louis Poinsot，他们在18世纪分别独立地研究和描述了这种陀螺的运动。这种情形为刚体动力学领域提供了重要的理论基础，并在许多相关学科中被广泛应用。

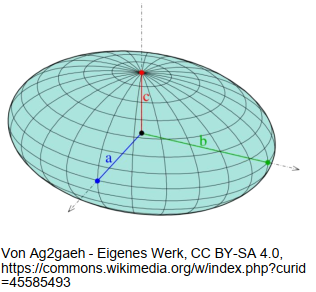
Jetzt wir der allgemeiner Fall mit drei unterschiedlichen Hauptmassenträgheitsmomenten untersucht (triaxiales Trägheitsellipsoid):

现在检查具有三个不同主要质量惯性矩的一般情况（三轴惯性椭球）：

Zwei Integrale des Systems sind einfach zu erkennen. Das erste Integral druck die Erhaltung der Energie des Systems aus. In diesem Fall ist das nur die kinetische Energie des Körpers.

系统的两个积分很容易辨认出来。第一个积分表示系统能量的守恒。在这种情况下，它只表示物体的动能。

\[\begin{aligned} & \omega_1 \dot{\omega}_1 J_{11}+\omega_2 \dot{\omega}_2 J_{22}+\omega_3 \dot{\omega}_3 J_{33}-\omega_1 \omega_2 \omega_3\left(J_{22}-J_{33}\right)-\omega_2 \omega_3 \omega_1\left(J_{33}-J_{11}\right)-\omega_3 \omega_2 \omega_1\left(J_{11}-J_{22}\right)=0 \\ & \omega_1 \dot{\omega}_1 J_{11}+\omega_2 \dot{\omega}_2 J_{22}+\omega_3 \dot{\omega}_3 J_{33}=0 \\ & \frac{d}{d t}\left(\omega_1^2 J_{11}+\omega_2^2 J_{22}+\omega_3^2 J_{33}\right)=0 \\ & \omega_1^2 J_{11}+\omega_2^2 J_{22}+\omega_3^2 J_{33}=\text { konst }=A \Omega^2 \end{aligned}\]

Das zweite Integral druckt die Erhaltung des Drehimpulses aus:

第二个积分表示角动量守恒：

\[\begin{aligned} & \dot{\omega}_1 J_{11}-\omega_2 \omega_3\left(J_{22}-J_{33}\right)=0 \\ & \dot{\omega}_2 J_{22}-\omega_3 \omega_1\left(J_{33}-J_{11}\right)=0 \\ & \dot{\omega}_3 J_{33}-\omega_2 \omega_1\left(J_{11}-J_{22}\right)=0 \\ & J_{11} \neq J_{22} \neq J_{33} \end{aligned}\] \[\begin{aligned} & \omega_1 \dot{\omega}_1 J_{11}^2+\omega_2 \dot{\omega}_2 J_{22}^2+\omega_3 \dot{\omega}_3 J_{33}^2-\omega_1 \omega_2 \omega_3 J_{11}\left(J_{22}-J_{33}\right)-\omega_2 \omega_3 \omega_1 J_{22}\left(J_{33}-J_{11}\right)-\omega_3 \omega_2 \omega_1 J_{33}\left(J_{11}-J_{22}\right)=0 \\ & \omega_1 \dot{\omega}_1 J_{11}^2+\omega_2 \dot{\omega}_2 J_{22}^2+\omega_3 \dot{\omega}_3 J_{33}^2-\omega_1 \omega_2 \omega_3\left(J_{11} J_{22}-J_{11} J_{33}+J_{22} J_{33}-J_{22} J_{11}+J_{33} J_{11}-J_{33} J_{22}\right)=0 \\ & \omega_1 \dot{\omega}_1 J_{11}^2+\omega_2 \dot{\omega}_2 J_{22}^2+\omega_3 \dot{\omega}_3 J_{33}^2=0 \\ & \frac{d}{d t}\left(\omega_1^2 J_{11}^2+\omega_2^2 J_{22}^2+\omega_3^2 J_{33}^2\right)=0 \\ & \omega_1^2 J_{11}^2+\omega_2^2 J_{22}^2+\omega_3^2 J_{33}^2=\text { konst }=A^2 \Omega^2 \quad A \text { und } \Omega \text { sind Integrationskonstanten. } \end{aligned}\]

Integrationskonstanten – 积分常数

Zwecks besserer Eindeutigkeit nehmen wir folgendes Verhältnis zwischen den Parameter an:

为了清楚起见，我们假设参数之间存在以下关系：

\[J_{11}<J_{22}<J_{33}\]

Aus der Definition der Parameter wird ersichtlich:

参数的定义显示：

\[\begin{aligned} & A=\frac{A^2 \Omega^2}{A \Omega^2}=\frac{\omega_1^2 J_{11}^2+\omega_2^2 J_{22}^2+\omega_3^2 J_{33}^2}{\omega_1^2 J_{11}+\omega_2^2 J_{22}+\omega_3^2 J_{33}} \quad \rightarrow \quad J_{11} \leq A \leq J_{33} \\ & \omega_1^2 J_{11}+\omega_2^2 J_{22}+\omega_3^2 J_{33}=\text { konst }=A \Omega^2 \mid \cdot J_{11} \\ & \omega_1^2 J_{11}^2+\omega_2^2 J_{22}^2+\omega_3^2 J_{33}^2=\text { konst }=A^2 \Omega^2 \\ & - \\ & \omega_2^2 J_{22}\left(J_{22}-J_{11}\right)+\omega_3^2 J_{33}\left(J_{33}-J_{11}\right)=A \Omega^2\left(A-J_{11}\right) \\ & \omega_3^2=\frac{A\left(A-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)} \Omega^2-\frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)} \omega_2^2 \\ & \omega_3^2=\frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)}(\underbrace{\frac{A\left(A-J_{11}\right)}{J_{22}\left(J_{22}-J_{11}\right)} \Omega^2-\omega_2^2}_{\lambda_3^2})=\frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)}\left(\lambda_3^2-\omega_2^2\right) \end{aligned}\]

Zwecks besserer Eindeutigkeit nehmen wir folgendes Verhältnis zwischen den Parameter an:

为了清楚起见，我们假设参数之间存在以下关系： Analog bekommt man

\[\begin{aligned} & \omega_1^2 J_{11}+\omega_2^2 J_{22}+\omega_3^2 J_{33}=\text { konst }=A \Omega^2 \mid \cdot J_{33} \\ & \omega_1^2 J_{11}^2+\omega_2^2 J_{22}^2+\omega_3^2 J_{33}^2=\text { konst }=A^2 \Omega^2 \\ & - \\ & \omega_1^2 J_{11}\left(J_{33}-J_{11}\right)+\omega_2^2 J_{22}\left(J_{33}-J_{22}\right)=A \Omega^2\left(J_{33}-A\right) \\ & \omega_1^2=\frac{A\left(J_{33}-A\right)}{J_{11}\left(J_{33}-J_{11}\right)} \Omega^2-\frac{J_{22}\left(J_{33}-J_{22}\right)}{J_{11}\left(J_{33}-J_{11}\right)} \omega_2^2 \\ & \omega_1^2=\frac{J_{22}\left(J_{33}-J_{22}\right)}{J_{11}\left(J_{33}-J_{11}\right)}(\underbrace{\frac{A\left(J_{33}-A\right)}{J_{22}\left(J_{33}-J_{22}\right)} \Omega^2}_{\lambda_1^2}-\omega_2^2)=\frac{J_{22}\left(J_{33}-J_{22}\right)}{J_{11}\left(J_{33}-J_{11}\right)}\left(\lambda_1^2-\omega_2^2\right) \end{aligned}\]

Diese Ausdrucke können wir in die letzte übriggebliebene Gleichung einsetzen: 我们可以将这些表达式代入最后剩下的等式：

\[\begin{aligned} & \dot{\omega}_2 J_{22}-\omega_3 \omega_1\left(J_{33}-J_{11}\right)=0 \\ & \left.\begin{array}{l} \omega_1^2=\frac{J_{22}\left(J_{33}-J_{22}\right)}{J_{11}\left(J_{33}-J_{11}\right)}\left(\lambda_1^2-\omega_2^2\right) \\ \omega_3^2=\frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)}\left(\lambda_3^2-\omega_2^2\right) \end{array}\right\} \\ & \omega_3 \omega_1= \pm \sqrt{\frac{J_{22}\left(J_{33}-J_{22}\right)}{J_{11}\left(J_{33}-J_{11}\right)} \frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)}} \sqrt{\left(\lambda_1^2-\omega_2^2\right)\left(\lambda_3^2-\omega_2^2\right)} \\ & \omega_3 \omega_1= \pm \frac{J_{22}}{\left(J_{33}-J_{11}\right)} \sqrt{\frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}} \sqrt{\left(\lambda_1^2-\omega_2^2\right)\left(\lambda_3^2-\omega_2^2\right)} \\ & \dot{\omega}_2 J_{22}= \pm \omega_3 \omega_1\left(J_{33}-J_{11}\right) \frac{J_{22}}{\left(J_{33}-J_{11}\right)} \sqrt{\frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}} \sqrt{\left(\lambda_1^2-\omega_2^2\right)\left(\lambda_3^2-\omega_2^2\right)} \\ & \dot{\omega}_2= \pm \sqrt{\frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}} \sqrt{\left(\lambda_1^2-\omega_2^2\right)\left(\lambda_3^2-\omega_2^2\right)} \\ & \end{aligned}\] \[\begin{aligned} & \dot{\omega}_2= \pm \sqrt{\frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}} \sqrt{\left(\lambda_1^2-\omega_2^2\right)\left(\lambda_3^2-\omega_2^2\right)} \\ & \frac{d \omega_2}{\sqrt{\left(\lambda_1^2-\omega_2^2\right)\left(\lambda_3^2-\omega_2^2\right)}}= \pm \sqrt{\frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}} d t \\ & \end{aligned}\]

Es wird beispielhaft der Fall $J_{22}<A<J_{33}$ untersucht. Es werden eine neue Variable und zwei neue Parameter eingeführt:

在研究 $J_{22}<A<J_{33}$ 的示例情况时，引入了一个新的变量和两个新的参数：

\[\begin{aligned} & \omega_2=\lambda_1 u \\ & k^2=\frac{\lambda_1^2}{\lambda_3^2}=\frac{\left(J_{22}-J_{11}\right)\left(J_{33}-A\right)}{\left(A-J_{11}\right)\left(J_{33}-J_{22}\right)}<1 \\ & \frac{\lambda_1 d u}{\lambda_1 \lambda_3 \sqrt{\left(1-u^2\right)\left(1-k^2 u^2\right)}}= \pm \sqrt{\frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}} d t \\ & n=\lambda_3 \sqrt{\frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}}=\Omega \sqrt{\frac{A\left(A-J_{11}\right)}{J_{22}\left(J_{22}-J_{11}\right)} \frac{\left(J_{33}-J_{22}\right)\left(J_{22}-J_{11}\right)}{J_{11} J_{33}}} \\ & =\Omega \sqrt{\frac{A\left(A-J_{11}\right)\left(J_{33}-J_{22}\right)}{J_{11} J_{22} J_{33}}} \end{aligned}\]

Damit kommen wir zur folgenden Lösung

这给我们带来了以下解决方案

\[\pm n\left(t-t_0\right)=\int_0^U \frac{d u}{\sqrt{\left(1-u^2\right)\left(1-k^2 u^2\right)}}\]

Weitere Transformation führt sofort zum elliptischen Integral:

进一步变换立即得到椭圆积分：

\[\begin{aligned} & u=\sin \Phi \\ & \pm n\left(t-t_0\right)=\int_0^{\Phi} \frac{\cos \vartheta d \vartheta}{\sqrt{1-\sin ^2 \vartheta} \sqrt{\left(1-k^2 \sin ^2 \vartheta\right)}} \\ & \pm n\left(t-t_0\right)=\int_0^{\Phi} \frac{d \vartheta}{\sqrt{\left(1-k^2 \sin ^2 \vartheta\right)}}=w(\Phi, k) \end{aligned}\]

Das ist das unvollständige elliptische Integral 1. Art. Sein Reziprok führt auf elliptische Funktionen von Jakobi.

这是第一类不完全椭圆积分，它的倒数导出Jakobi的椭圆函数。

Definition (Legendre-Normalform) 定义（勒让德范式）

\[w(\Phi, k)=\int_0^{\Phi} \frac{d \vartheta}{\sqrt{\left(1-k^2 \sin ^2 \vartheta\right)}}\]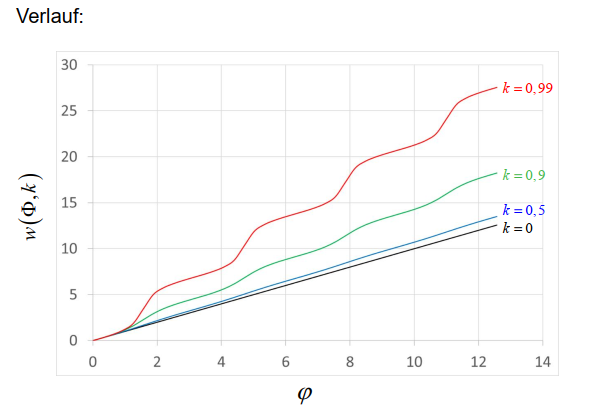

Reziprok davon wird als elliptische Amplitude bezeichnet

这个的倒数称为椭圆振幅

\[w(\Phi, k)=\int_0^{\Phi} \frac{d \vartheta}{\sqrt{\left(1-k^2 \sin ^2 \vartheta\right)}} \rightarrow \quad \Phi(w)=a m(w)\]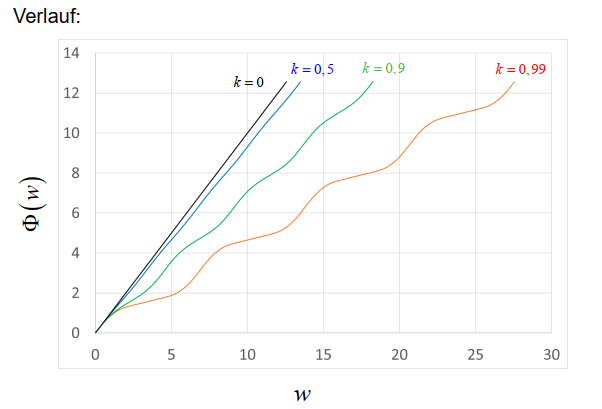

Ausgehend von dieser Funktion werden die elliptischen Funktionen von Jacobi eingeführt:

基于此函数，引入雅可比的椭圆函数：

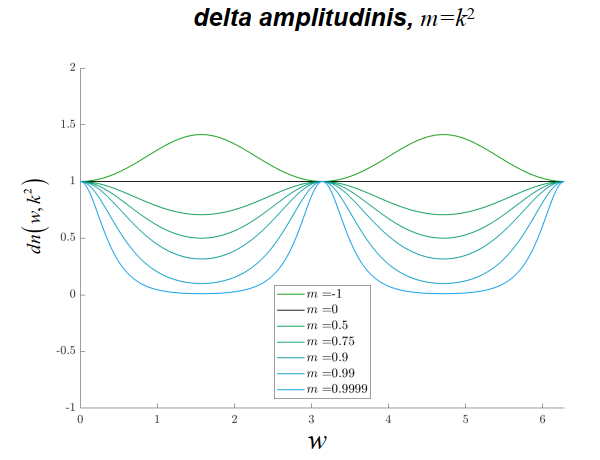
\[\begin{aligned} & \operatorname{sn}(w)=\sin \Phi=\sin (a m(w)) \\ & c n(w)=\cos \Phi=\cos (a m(w)) \\ & d n(w)=\sqrt{1-k^2 \sin ^2 \Phi}=\sqrt{1-k^2 \operatorname{sn}^2(w)} \end{aligned}\]

Sie werden als sinus amplitudinis, cosinus amplitudinis und delta amplitudinis bezeichnet.

Diese Funktionen sind periodisch mit der Periode, die vom Parameter k abhängig ist. Die Abhängigkeit hängt mit dem kompletten elliptischen Integral zusammen:

它们被称为正弦波、余弦波和三角波。

这些函数是周期性的，周期取决于参数 k。依赖关系与完全椭圆积分有关：

\[\begin{aligned} & K(k)=\int_0^{\frac{\pi}{2}} \frac{d \vartheta}{\sqrt{\left(1-k^2 \sin ^2 \vartheta\right)}} \\ & d n(w+2 K)=d n(w) \\ & \operatorname{sn}(w+4 K)=\operatorname{sn}(w) \\ & c n(w+4 K)=c n(w) \\ & s n^2(w)+c n^2(w)=1 \end{aligned}\]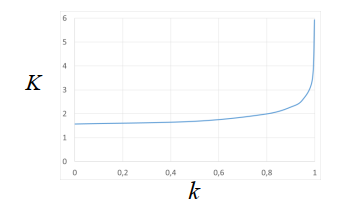

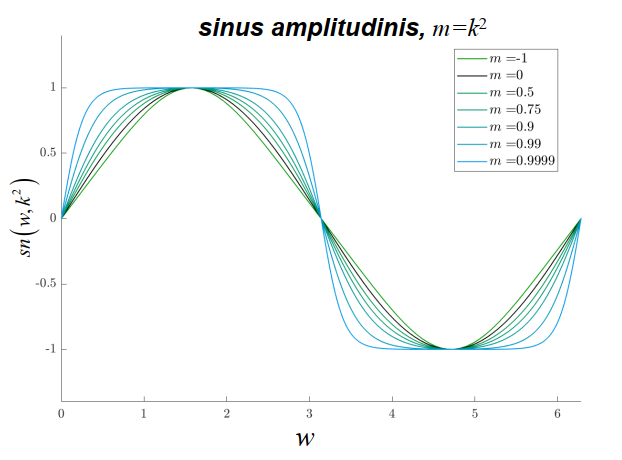
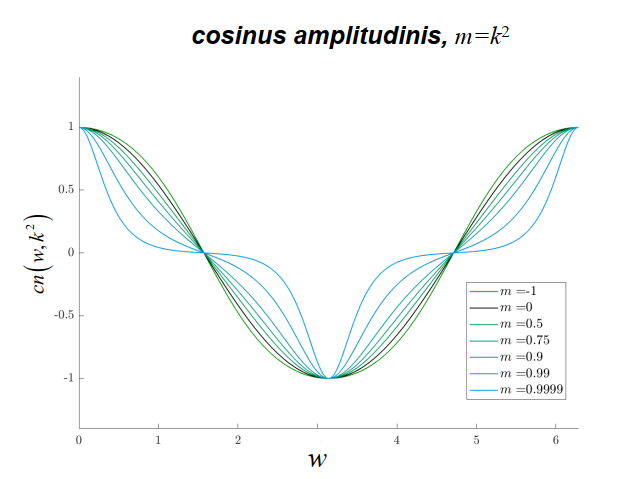
Mithilfe dieser Funktionen können wir die Komponenten der Winkelgeschwindigkeit sofort bestimmen:

使用这些函数，我们可以立即确定角速度的分量：

\[\begin{aligned} & \omega_2= \pm \lambda_1 \operatorname{sn}\left(n\left(t-t_0\right)\right) \\ & \omega_1= \pm \sqrt{\frac{J_{22}\left(J_{33}-J_{22}\right)}{J_{11}\left(J_{33}-J_{11}\right)}} \sqrt{\lambda_1^2-\omega_2^2} \quad \rightarrow \\ & \omega_1= \pm \sqrt{\frac{J_{22}\left(J_{33}-J_{22}\right)}{J_{11}\left(J_{33}-J_{11}\right)}} \lambda_1 \operatorname{cn}\left(n\left(t-t_0\right)\right) \\ & \omega_3= \pm \frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)} \sqrt{\lambda_3^2-\omega_2^2} \quad \rightarrow \\ & \omega_3= \pm \frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)} \lambda_3 \sqrt{1-k^2 s^2\left(n\left(t-t_0\right)\right)} \rightarrow \\ & \omega_3= \pm \frac{J_{22}\left(J_{22}-J_{11}\right)}{J_{33}\left(J_{33}-J_{11}\right)} \lambda_3 d n\left(n\left(t-t_0\right)\right) \\ & \end{aligned}\]

Kinematische Teilaufgabe führt sofort zu einer weiteren Quadratur. 运动学子任务立即导致另一个正交。

\[\begin{aligned} & L \sin \varphi \sin \theta=J_{11} \omega_1 \\ & L \cos \varphi \sin \theta=J_{22} \omega_2 \\ & L \cos \theta=J_{33} \omega_3 \\ & \theta=\arccos \left(\frac{J_{33} \omega_3}{L}\right) \\ & \tan \varphi=\frac{J_{11} \omega_1}{J_{22} \omega_2} \rightarrow \quad \varphi=\arctan \left(\frac{J_{11} \omega_1}{J_{22} \omega_2}\right) \end{aligned}\]

Für Winkel $\varphi$ bleibt eine Differentialgleichung 1. Ordnung, die bei Bedarf integriert werden kann:

角度 $\varphi$ 的一阶微分方程仍然存在，必要时可以对其进行积分：

\[\dot{\psi} \cos \theta+\dot{\varphi}=\omega_3 \quad \rightarrow \quad \dot{\psi}=\frac{\omega_3-\dot{\varphi}}{\cos \theta}=L \frac{J_{11} \omega_1^2+J_{11} \omega_2^2}{J_{11}^2 \omega_1^2+J_{22}^2 \omega_2^2}\]

Der zweite Fall $J_{11}<A<J_{22}$ kann analog untersucht werden.

第二种情况$J_{11}<A<J_{22}$可以类推.

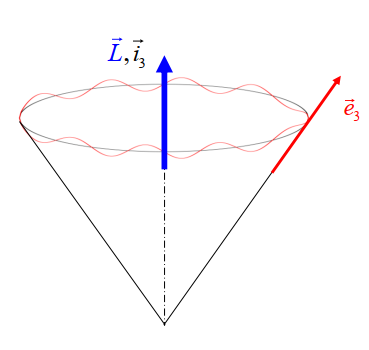
Qualitativer Charakter der Bewegung:

Ein rotationssymmetrischer Körper bewegt sich so, dass der Nutationswinkel konstant bleibt. Die Geschwindigkeiten der Präzession und der Drehung um die eigene Achse bleiben auch konstant.

Bei einem nicht rotationssymmetrischen Körper (einem dreiachsigen Ellipsoid) wird das alles gestört. Die Geschwindigkeiten der Präzession und der Drehung um die eigene Achse werden zeitvariabel. Auch der Nutationswinkel wird zeitveränderlich, aber alle kinematischen Größen der Bewegung können in geschlossener Form (aber nicht in elementaren Funktionen) bestimmt werden.

运动的定性特征：

对于一个具有旋转对称性的物体，其运动使得进动角保持恒定。进动和自转的速度也保持恒定。

然而，对于一个非旋转对称的物体（如一个三轴椭球体），这些特性会受到扰动。进动和自转的速度将随时间变化。进动角度也会随时间变化。尽管如此，运动的所有运动学量可以以闭合形式（但不是基本函数）确定

李文博

高傲的电工李