机器学习 Machine Learning - Neural Networks 神经网络

2023-06-14 | 阅读：次

Neural Networks 神经网络

We will learn today… - What a (deep) neural network is
- How do we train it?
- … which requires a calculus refresher ☺
- Why is everybody talking about it?
- Various ways to accelerate gradient descent
- Practical tips and tricks for training NNs

我们今天将学习以下内容：

- 什么是（深度）神经网络
- 如何训练神经网络？
- 这需要温习一下微积分 ☺
- 为什么大家都在谈论它？
- 加速梯度下降的各种方法
- 训练神经网络的实际技巧和诀窍

Today‘s Agenda!

- What is a Neuron?
- Architectures and Activation Functions
- Loss-functions
- Backpropagation and the Chain Rule
- Computation graphs

Advanced Topics: - Accelerating gradient descent - Regularization in Neural Networks - Practical considerations

今天的议程如下：

- 什么是神经元？
- 架构和激活函数
- 损失函数
- 反向传播和链式法则
- 计算图

深入话题:
- 加速梯度下降
- 神经网络中的正则化
- 实际考虑因素

Biological Inspiration: The brain 生物学灵感：大脑

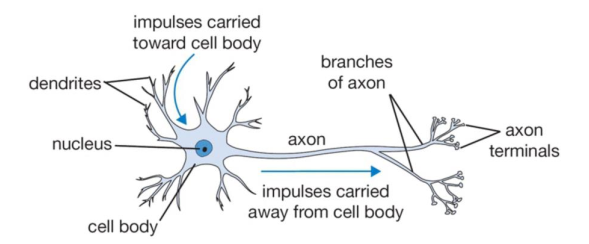
A neuron is the basic computational unit of the brain:

神经元是大脑的基本计算单元：

Our brain has ~ 1011 neurons
Each neuron is connected to ~ 104 other neurons (via synapses)
Synapses have different connectivity
Approx. model: Input impulses are weighted by synapse strength and added up
我们的大脑有大约10^11个神经元。
每个神经元通过大约10^4个突触连接到其他神经元。
突触具有不同的连接方式。
近似模型：输入脉冲通过突触的强度加权并相加。

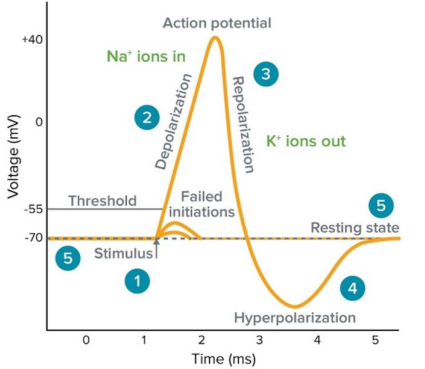
Neurons receive input signals and accumulate voltage. After some threshold they will fire spiking responses (highly non-linear response).

神经元接收输入信号并积累电压。在达到某个阈值后，它们将激发尖峰响应（高度非线性响应）。

Artificial Neurons 人工神经元

For neural nets, we use a much simpler unit (neuron, perceptron):

对于神经网络，我们使用更简单的单元（神经元、感知器）：

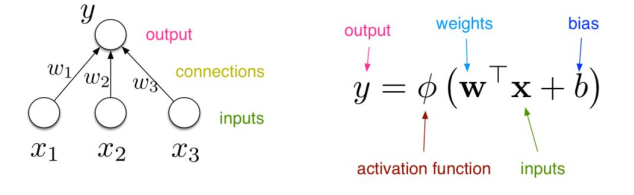
3 ingredients: - Weighting of the input - Summation - Non-linear activation function

三个要素： - 输入的加权 - 总和计算 - 非线性激活函数

Example we already know:

Logistic regression 逻辑回归

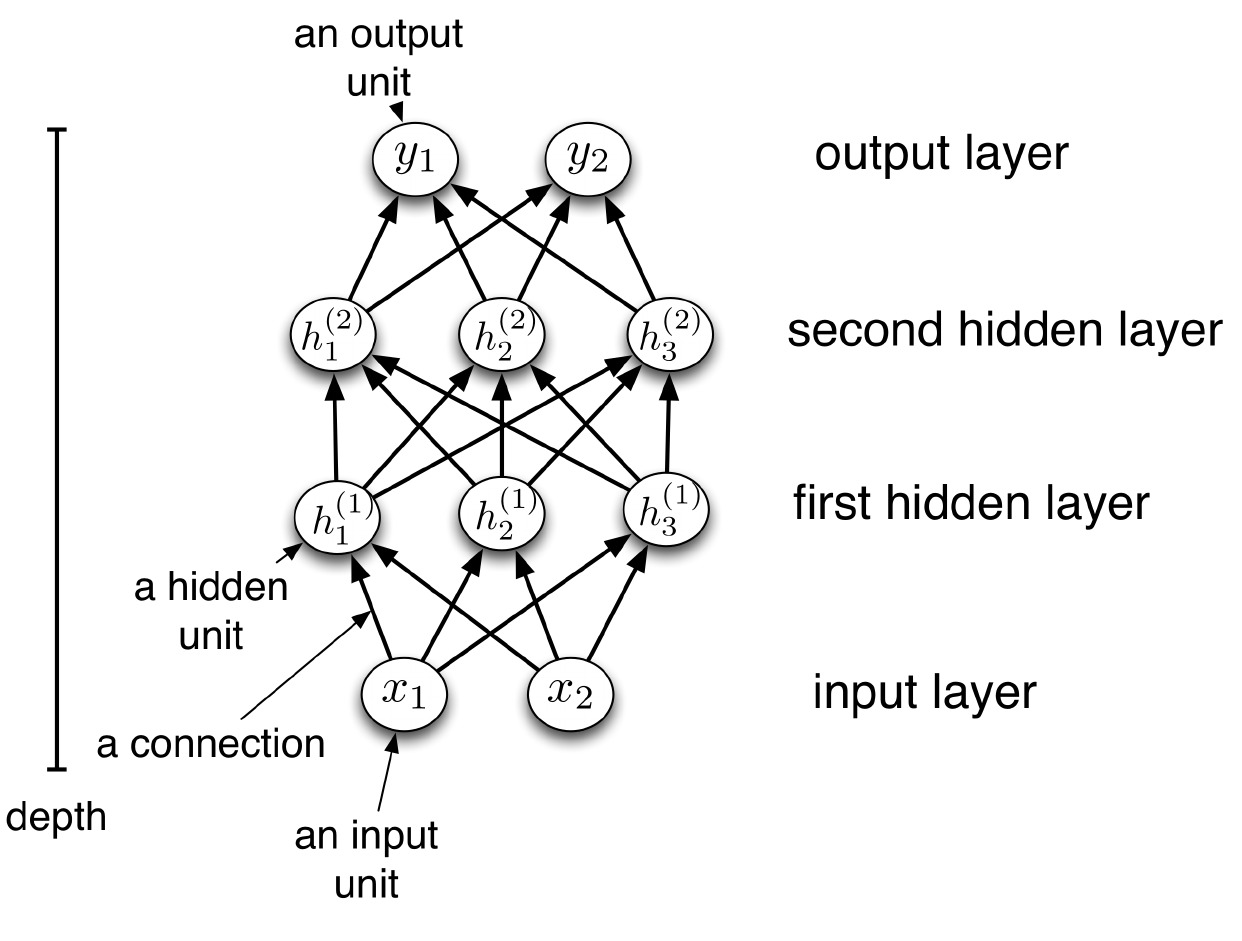
\[y=\sigma\left(\mathbf{w}^T \mathbf{x}+b\right)\]

Feedforward Neural Networks 前馈神经网络

Building a network:

We can connect lots of units together into a directed acyclic graph.
This gives a feed-forward neural network. That’s in contrast to recurrent neural networks, which can have cycles.
Typically, units are grouped together into layers.
Each layer connects N input units to M output units.
In the simplest case, all input units are connected to all output units. We call this a fully connected layer.
Note: the inputs and outputs for a layer are distinct from the inputs and outputs to the network

构建一个网络：

我们可以将很多单元连接在一起形成一个有向无环图。
这就得到了一个前馈神经网络。与循环神经网络形成对比，后者可以有循环。
通常，单元被分组成层。
每一层将N个输入单元连接到M个输出单元。
在最简单的情况下，所有输入单元都连接到所有输出单元。我们称之为全连接层。
注意：层的输入和输出与网络的输入和输出是不同的。

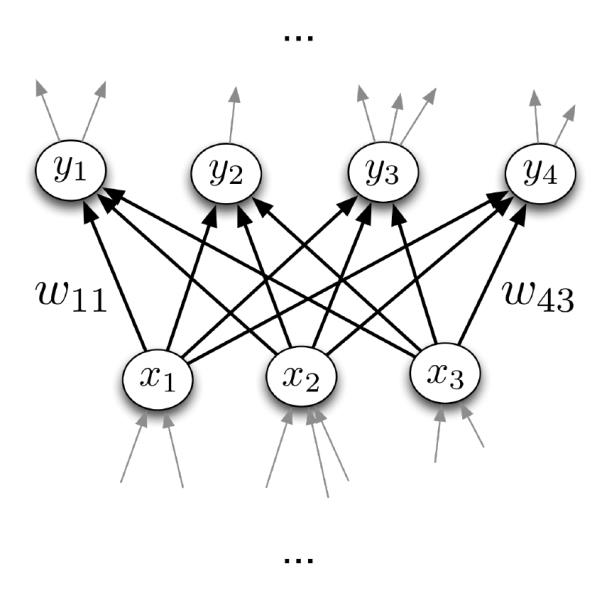
I.e., each layer has a M x N weight matrix W
Equation in matrix form: $\mathbf{y}=\phi(\mathbf{W} \mathbf{x}+\mathbf{b})$
- Output units are a function of input units
Feedforward neural networks are also often called multi-layer perceptrons (MLPs)
每一层具有一个大小为M x N的权重矩阵W。
以矩阵形式的方程为：$\mathbf{y}=\phi(\mathbf{W} \mathbf{x}+\mathbf{b})$
- 输出单元是输入单元的函数。
前馈神经网络通常也被称为多层感知器（MLP）

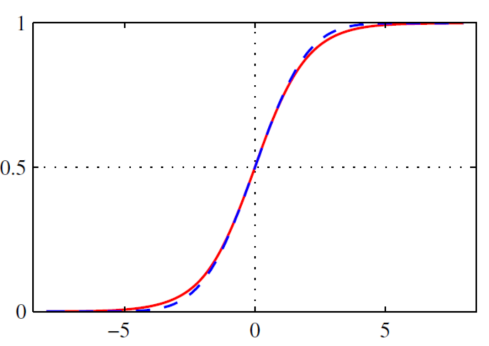
Activation funcitons 激活函数

Different activation functions for introducing non-linearities: 引入非线性的不同激活函数：

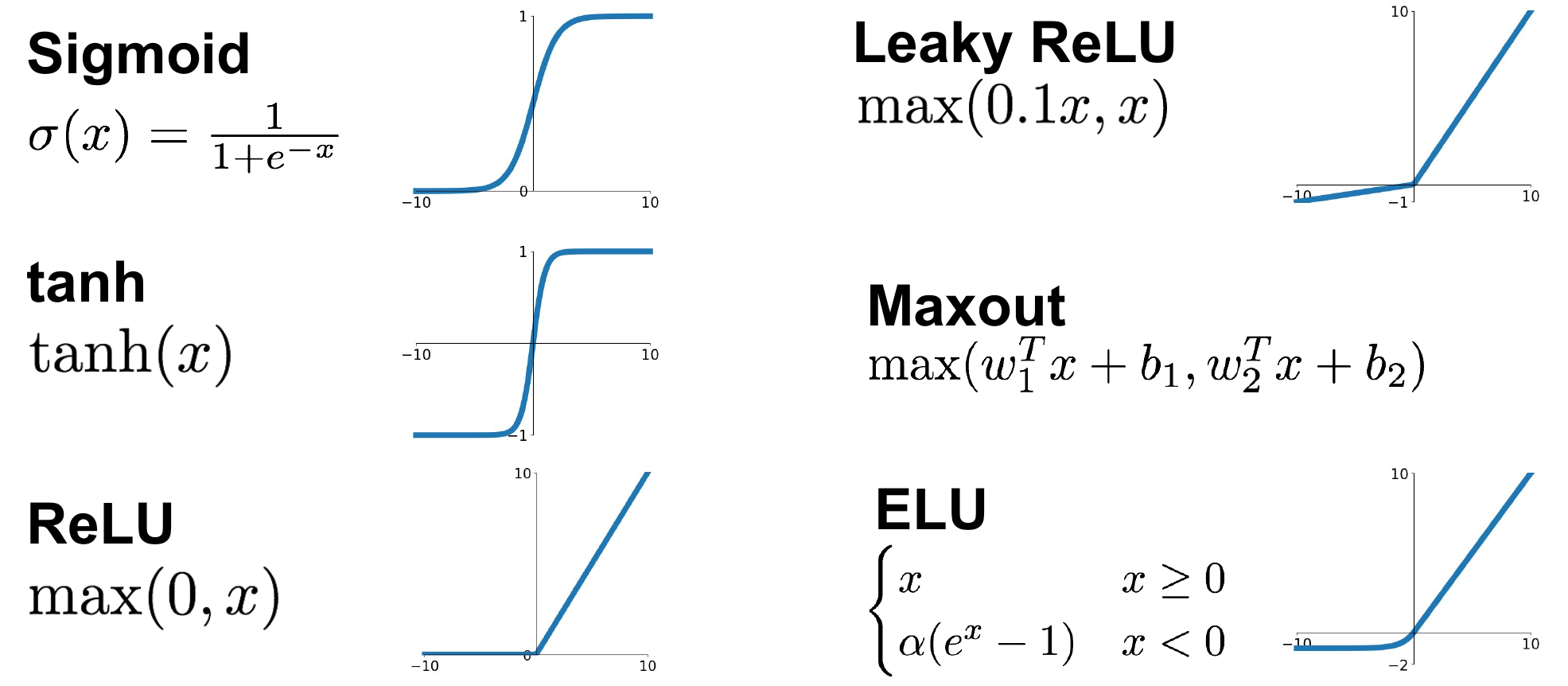
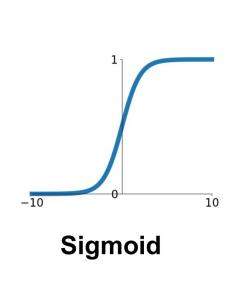
计算：

\[\sigma(x)=\frac{1}{1+\exp (-x)}\]

将数字压缩到范围[0,1]
从历史上来看它们非常流行，因为它们可以很好地解释为神经元的饱和“发射率”

常用的激活函数（如Sigmoid函数）在输入值较大或较小的情况下会饱和，即输出值接近0或1，并具有类似于神经元发射的特性。因此，这些激活函数的输出值可以被解释为神经元的饱和“发射率”。

问题：

饱和的神经元会使得梯度消失
Sigmoid函数的输出不以零为中心（对于初始化很重要）
exp()计算耗费资源

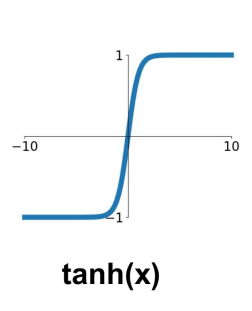
将数字压缩到范围[-1,1]
✓ 以零为中心（很好）
× 当饱和时仍然会消失梯度

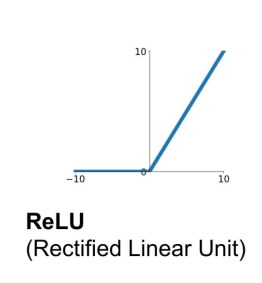
修正线性单元（Rectified Linear Unit，ReLU）

计算： $f(x)=\max (0, x)$

✓ 不会饱和（在正区间内）
✓ 计算效率非常高
✓ 在实践中比sigmoid/tanh函数收敛速度快得多（例如，快6倍）

× 输出不以零为中心
× 对于x < 0没有梯度

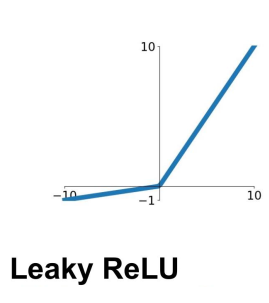
计算： $f(x)=\max (0.1 x, x)$

✓ 不会饱和
✓ 计算效率高
✓ 在实践中收敛速度比sigmoid/tanh函数快很多！（例如，6倍）
✓ 不会“消失”

Parametric Rectifier (PReLu):
参数整流器 (PReLu)：

计算： $f(x)=\max (\alpha x, x)$

Also learn alpha

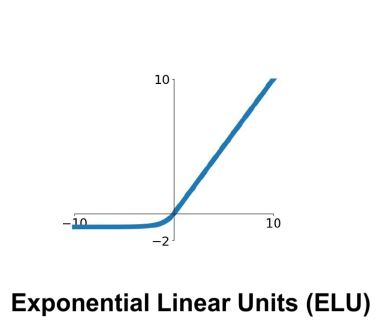
指数线性单元

计算：

\[f(x)= \begin{cases}x & \text { if } x>0 \\ \alpha(\exp (x)-1) & \text { if } x \leq 0\end{cases}\]

其中，alpha是一个预定义的常数，通常取一个较小的正数。

✓ 具有ReLU的所有优点
✓ 输出接近零均值
× 计算过程中需要使用exp()函数

In practice:

使用ReLU。在学习率和初始化时要小心。

对于学习率（learning rate），选择一个合适的值非常重要。过大的学习率可能导致训练不稳定或发散，而过小的学习率可能导致收敛速度过慢。

对于初始化（initialization），权重和偏置的初始值也需要谨慎选择。使用不合适的初始化方法可能导致梯度消失或梯度爆炸等问题，影响网络的训练效果。对于使用ReLU的网络，一种常见的初始化方法是使用较小的随机值，如从均匀分布或正态分布中采样得到的值。
尝试使用Leaky ReLU / ELU。
尝试使用tanh函数，但不要期望太多。
不要使用sigmoid函数。
- sigmoid函数仅在分类问题的输出激活中使用。

Formalisation:

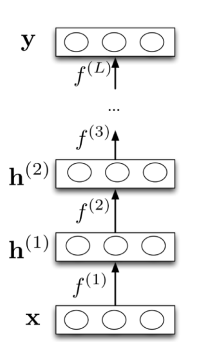
每层计算一个函数，因此网络计算函数的组合：

\[\begin{aligned} \mathbf{h}^{(1)} & =f^{(1)}(\mathbf{x}) \\ \mathbf{h}^{(2)} & =f^{(2)}\left(\mathbf{h}^{(1)}\right) \\ \vdots & \end{aligned}\]

或者更简单地：

\[\begin{aligned} & \mathbf{y}=f^{(L)}\left(\mathbf{h}^{(L-1)}\right) \\ & \mathbf{y}=f^L \circ f^{L-1} \circ \ldots f^{(1)}(\mathbf{x}) \end{aligned}\]

神经网络提供模块化：我们可以将每一层的计算实现为一个黑盒子

Example: XOR 异或

设计一个实现 XOR 的网络：

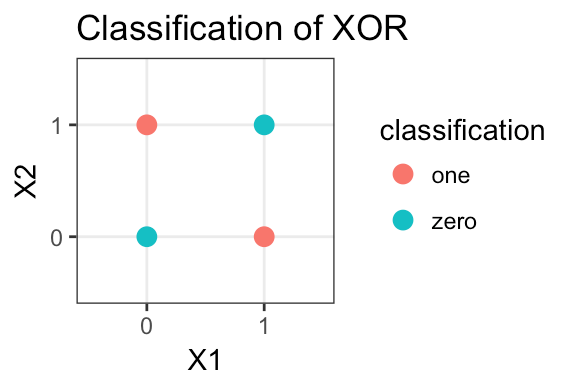
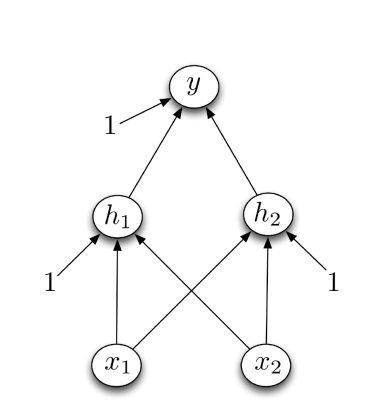
单个单元无法计算!
经典的例子，为什么我们需要多层次

XOR in terms of elemental operations:

XOR(a,b) = (a OR b) AND NOT (a AND b)

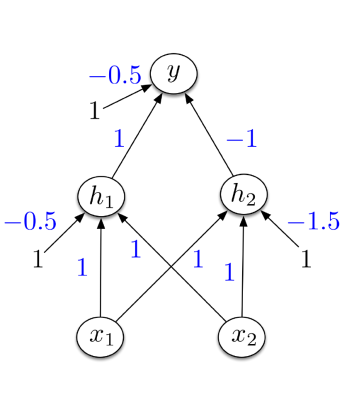
设计一个实现XOR的网络：

激活函数的硬阈值，x1和x2是二进制的
h1 计算 x1 OR x2
h2 计算 x1 AND x2
y 计算 h1 AND NOT h2

Deep Architectures深层架构

为什么我们需要深入？

任何线性层序列都可以用单个线性层等效地表示

\[\mathbf{y}=\underbrace{\mathbf{W}^{(3)} \mathbf{W}^{(2)} \mathbf{W}^{(1)}}_{\tilde{\mathbf{W}}} \mathbf{x}\]

即，我们需要非线性，以利用多个层次

具有非线性激活函数的FF-NN是通用函数近似器：
- 给定一个潜在的无限量的单元，它们可以任意地逼近任何函数
- 通用函数逼近定理：单层就足以实现 “普适性”

那么，单层是否足够？

尽管通用函数逼近定理表示单层理论上足够，但实际上我们需要指数级（与输入维度成正比）的神经元数量才能实现这一点。
- 如果可以学习任何函数，那么结果很可能会过拟合。
相反，多层网络可以用更少的神经元实现类似的效果。
- 紧凑的表示方式比”通用表示”更有效。

Loss-functions 损失函数

训练神经网络的目标函数：

通用的机器学习方法：逐样本损失 + 正则化惩罚

\[\boldsymbol{\theta}^*=\underset{\text { parameters } \boldsymbol{\theta}}{\arg \min } \sum_{i=1}^N l\left(\boldsymbol{x}_i, \boldsymbol{\theta}\right)+\lambda \text { penalty }(\boldsymbol{\theta})\]

对于不同的任务，损失函数和输出激活函数的选择有所不同：

回归任务（Regression）：通常使用均方误差（Mean Squared Error）作为损失函数，输出激活函数可以是线性函数或恒等函数。
二分类任务（Binary Classification）：常见的损失函数包括二元交叉熵（Binary Cross-Entropy）或对数损失（Log Loss），输出激活函数通常选择sigmoid函数。
多类别分类任务（Multi-class Classification）：常用的损失函数是多类别交叉熵（Categorical Cross-Entropy），输出激活函数则通常选择softmax函数。

Regression 回归

Output layer: Deterministic 决定性 linear 线性 $$ \mathbf{f}=\mathbf{W}^{(L)} \mathbf{h}^{(L-1)}+\boldsymbol{b}^{(L)} $$ Loss： squared error 方差 $$ l_i\left(\mathbf{x}_i, \boldsymbol{\theta}\right)=\frac{1}{2}\left(\mathbf{f}\left(\mathbf{x}_i\right)-\mathbf{y}_i\right)^2 $$

Probabilistic 概率性 linear Gaussian $$ p(\mathbf{y} \mid \mathbf{x})=\mathcal{N}\left(\mathbf{y} \mid \mathbf{W}^{(L)} \mathbf{h}^{(L-1)}+\mathbf{b}^{(L)}, \mathbf{\Sigma}\right) $$
negative log-likelihood 负对数似然 $$ l_i\left(\mathbf{x}_i, \boldsymbol{\theta}\right)=-\log \mathcal{N}\left(\mathbf{y}_i \mid \boldsymbol{\mu}\left(\mathbf{x}_i\right), \boldsymbol{\Sigma}\right) $$

Binary classification 二元分类

Output layer: Deterministic 决定性 linear 线性 $$ f=\mathbf{W}^{(L)} \mathbf{h}^{(L-1)}+b^{(L)} $$ Loss function hinge-loss 铰链损失 $$ l\left(\mathbf{x}_i, \boldsymbol{\theta}\right)=\max \left(0,1-y_i f\left(\boldsymbol{x}_i\right)\right) $$

Probabilistic 概率性 sigmoid $$ f=\sigma\left(\mathbf{W}^{(L)} \mathbf{h}^{(L-1)}+b^{(L)}\right) $$
neg-loglike 负对数似然 $$ \begin{aligned} l_i\left(\mathbf{x}_i, \boldsymbol{\theta}\right)= & -c_i \log f\left(\mathbf{x}_i\right)-\left(1-c_i\right) \log \left(1-f\left(\mathbf{x}_i\right)\right) \end{aligned} $$

其中$y_i$是 -1/+1 labels, $c_i$ 是0/1 labels。

Multi-class classification 多类别分类

Output layer: Deterministic 决定性 linear 线性 $$ \mathbf{f}=\mathbf{W}^{(L)} \mathbf{h}^{(L-1)}+\mathbf{b}^{(L)} $$ Loss function Multi-class SVM loss 多类 SVM 损失

Not covered

Probabilistic 概率性 sigmoid $$ \mathbf{f}=\operatorname{softmax}\left(\mathbf{W}^{(L)} \mathbf{h}^{(L-1)}+\mathbf{b}^{(L)}\right) $$
neg-loglike 负对数似然 $$ l_i\left(\mathbf{x}_i, \boldsymbol{\theta}\right)=-\sum_{k=1}^K \boldsymbol{h}_{c_i, k} \log y_k\left(\mathbf{x}_i\right) $$

其中 $\boldsymbol{h}_{c_i, k}$ 是 one hot coding

One-hot encoding是一种常用的数据预处理技术，用于将离散特征表示为二进制向量的形式。它常用于机器学习和深度学习任务中，特别是当特征数据中包含分类变量时。

在One-hot encoding中，如果一个特征具有n个不同的类别，那么它将被表示为一个长度为n的二进制向量，其中只有一个位置为1，其他位置都为0。被设置为1的位置对应于该特征所属的类别。

这样的编码方式有助于解决以下问题：

解决分类变量的数值化问题：分类变量通常无法直接用于机器学习算法，因为算法通常期望输入是数值型数据。One-hot encoding可以将分类变量转换为数值型数据，使其适用于算法的处理。

避免特征之间的顺序关系：One-hot encoding将每个类别都独立地表示为一个二进制向量，不考虑类别之间的顺序关系。这在一些情况下是有益的，例如避免算法错误地学习到类别之间的顺序或大小关系。

需要注意的是，当原始特征具有大量类别时，One-hot encoding会导致特征空间的维度增加，可能会导致稀疏矩阵和计算资源的浪费。在处理高维稀疏数据时，可能需要考虑其他的特征编码方法。

在实践中，可以使用多种编程语言和库来执行One-hot encoding，例如Python中的scikit-learn、pandas和TensorFlow等。

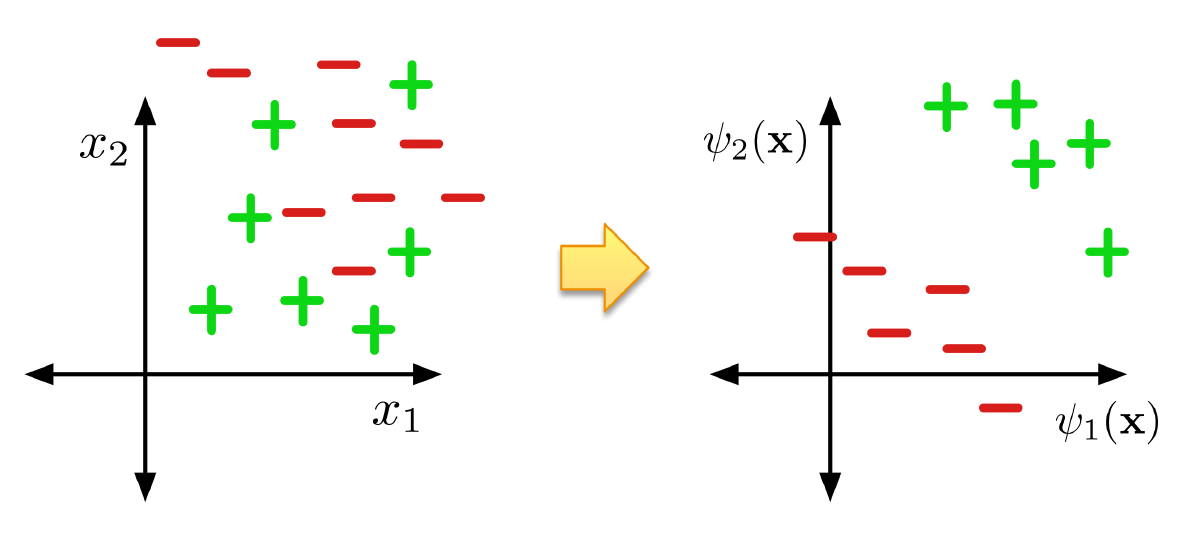
Feature Learning 特征学习

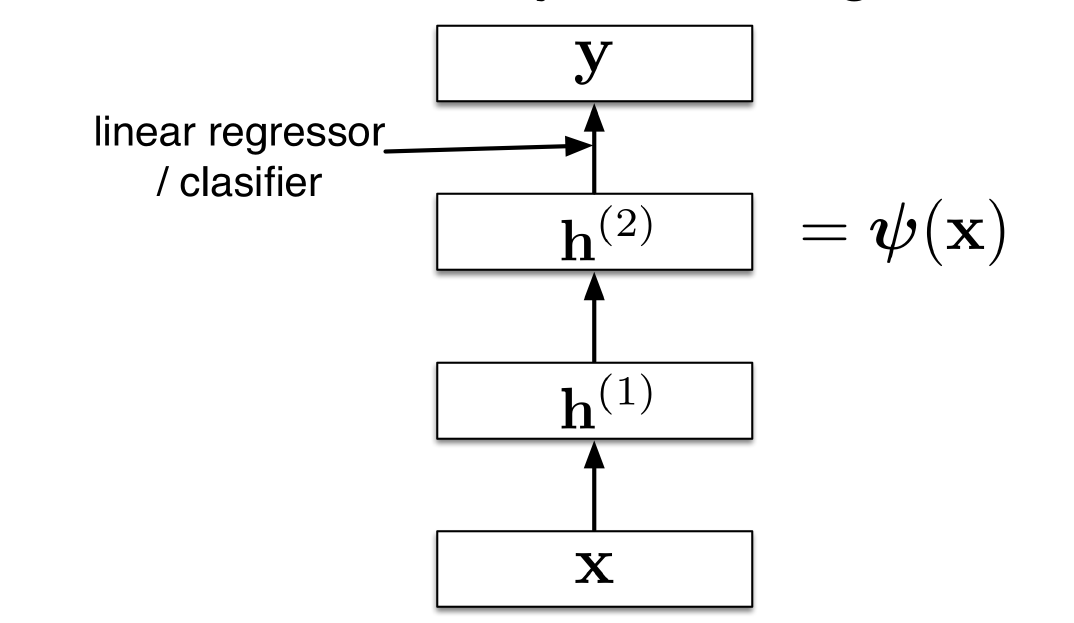
神经网络可以被看作是一种学习特征的方式

最后一层是标准的线性回归/分类层

网络学习特征$\psi(\mathbf{x})$使得线性回归/分类可以解决它

李文博

高傲的电工李