Chapter 8: Behavior Recognition 行为识别

今天我们讨论行为识别这一章节。

这是这一章节的参考文献列表，我们主要涉及隐马尔可夫模型，因此主要参考文献是关于隐马尔可夫模型及其在各种应用中的使用方法的教材。您可以考虑阅读Witten和Frank关于人工智能的书籍，其中包含了关于隐马尔可夫模型的章节。还有一本德语书，主要介绍了隐马尔可夫模型在各种应用领域的基本算法。还有一篇由Rabiner撰写的关于隐马尔可夫模型及其在语音识别中的应用的教程。虽然我们在这里不涉及语音识别，但所有这些方法也可以用于自动驾驶车辆的行为识别。第四和第五篇论文更侧重于车辆和交通场景的主题，它们描述了如何使用隐马尔可夫模型进行行为识别。

在我们开始讨论这些方法之前，让我们看一些在高速公路场景中使用我们的实验车辆拍摄的图片。在所有这些图片中，问题是：某辆车会不会变道，还是保持在原车道上。在第一张图片中，这辆车总是用橙色圆圈标记，所以这次是小型乘用车在卡车后面。问题是：这辆乘用车会不会变道，还是会保持在原车道上。

我们也许对驾驶应该有一些经验，也在高速公路上驾驶过，并且对这辆车会怎么做可能有一些想法。在这种情况下，可能有一些论点支持这辆车超车，也可能有一些论点认为它不会超车。你们可以猜测在这种情况下会发生什么，这辆车会在自己到达相应位置之前超车卡车并变道，还是会保持在原车道上，至少直到自己超过主车道上的车辆。这就是初始情况，现在让我们通过这些图片来观察一下。视频中的情况如下：再次，你可以猜测这辆车会做什么，也许在第一张图片上你猜测这辆车会变道或更有可能变道，看到这张图片，你可能会修改你的期望，可能会说它不太可能在自己前面的车辆面前变道。

如果我们再往下看一步，情况是这样的。现在明显地，这辆车不太可能超车。还不是完全不可能，但不太可能。当然，现在我们可以看到发生了什么，这辆车没有变道，它一直跟着卡车。

现在我们来看一下不同的情况。再次，我们看到前面有一辆在我们车道上行驶的乘用车，我们想猜测这辆车会不会变道。如果你仔细观察，你会发现在这辆车的前面也有一辆卡车。

一段时间后，情况是这样的。现在我们可以看到，这辆车前面甚至还有另一辆车，并且我们也可以看到这两辆乘用车并不在同一条线上，而我们想要预测的车辆已经稍微偏向左边。现在我们可以看到，它变道了，实际上它正在变道，穿过两个车道之间的中央线，结果是这辆车现在在左车道上。

第三个例子，我们再次关注右车道上的黑色车辆，它会变道吗？也许你已经说不太可能，因为没有理由让这辆车变道，前面没有障碍物或慢车。如果我们跟随这个视频，我们会发现最初的猜测是正确的，它没有变道。

第四个例子，我们再次关注右车道上的金属车辆，它跟随前面的卡车。观察这种情况，它会变道吗？很难说，你可以自己猜测。一段时间后，情况变成这样，现在明显地，这辆车确实变道了。

对我来说，至少当我看到第一张图片时，这有些出乎意料，考虑到整个情况。现在我们可以讨论一下，是哪些特征使我们能够预测一辆车的未来行为。

当然，如果要实现自动驾驶，行为识别非常重要。每辆车都与其他交通参与者互动，因此能够预测这些交通参与者在接下来的几秒钟内打算做什么非常重要，因此我们需要行为识别。行为识别基于各种技术的组合，首先我们需要从传感器数据中获取不同的特征。特征是我们可以从视频数据等中提取的信息。有很多可能的特征，通常我们需要多个特征，并将它们组合起来。每个特征本身可能是模棱两可的，因为可能会出现多种可能的情况。只有特征的组合可能会导致对实际发生的情况有一个明确的猜测。当然，这些特征发生的时间顺序也很重要，相同的特征以不同的时间顺序可能意味着完全不同的活动。

通过一个例子来阐明这一点，即在高速公路上的变道行为，就像在本章开头的图片中看到的那样。有许多特征，例如我们可以观察车辆的转向灯，它们可能开启、关闭、闪烁向左或向右。我们可能考虑车辆的横向位置，它是靠近车道中心线还是靠近车道边界。与前方车辆的距离也可能相关，以及与前方车辆的速度差和与邻近车道的速度差。我们可能检查邻近车道上是否有空隙，这是变道的先决条件，或者是否没有空隙。最后，我们还可以考虑车辆与预期速度的速度差。当然，我们不知道预期速度是多少，但我们可以猜测预期速度，或者至少从图像中的一些特征中得到一些关于预期速度的想法。例如，在高速公路上，根据法律，卡车的速度限制为每小时80公里，因此我们可以推断，卡车驾驶员通常打算以约80公里每小时的速度行驶。如果观察到一辆跑车，我们当然不会认为跑车驾驶员的期望速度是80公里每小时，而是可能是130公里每小时、150公里每小时甚至更高。因此，有些特征使我们至少能够大致猜测出这样一个期望速度。 车道变道的时间顺序可以描述为四个阶段的序列。第一个是我们跟随主车道，然后我们准备变道，打开转向灯，可能还调整速度以适应邻近车道，然后进行车道变道，最后跟随新的车道。

现在有三个问题需要解决：如何对行为的元素序列进行建模、如何对观测的不确定性和模糊性进行建模，以及如何利用这种建模来得出结论和猜测当前的行为。从科学的角度来看，对这个问题有几个答案。在本讲座中，我们将重点讨论隐马尔可夫模型。另一种选择是深度学习方法，但在这种情况下，我们将坚持使用隐马尔可夫模型。我们已经知道隐马尔可夫模型是什么，它是一个离散的随机状态转移系统，它的观测和后继状态完全取决于当前状态，而不取决于先前的状态或观测。这在第五章中介绍过。下面的两个公式描述了上面提到的独立假设。

如果要将隐马尔可夫模型用于行为识别，我们将车辆的行为建模为一系列状态。每个状态都对应车辆的某种活动，通常发生的序列由状态转移概率来建模，这意味着那些在实践中通常连续发生的活动或行为块具有较大的转移概率，而那些在实践中非常不可能连续发生的组合或序列具有非常小的转移概率。观测由隐马尔可夫模型中引入的测量变量来描述，观测模型描述了在哪种情况下观测发生以及观测发生的概率如何模型化了状态与观测之间的关系。

让我们来讨论一个非常简单的驾驶场景的案例，我们假设我们在一条只有一条车道的高速公路上行驶，因此不能变道，只能跟随主车道。尽管如此，我们可能能够区分两种不同的状态。一种是我们以期望的速度行驶，我们称之为自由行驶状态，因为除了法律法规之外，没有其他交通参与者以某种方式与我们互动，迫使我们改变速度。另一种状态是我们跟随前车，我们将其称为跟随状态，这意味着前方车辆以比我们期望的速度更慢行驶，迫使我们减速与前方车辆保持相同的速度。

我们可以将其建模为两个状态，并绘制状态转移图。每个状态都变成一个方框，然后用箭头连接这两个方框，表示可能和不可能的转换。箭头的粗细还表示了转换的可能性。比如说保持自由行驶状态的可能性要远大于转变为跟车状态的可能性。需要注意的是，隐马尔可夫模型假设我们有一个固定的离散时间表，即每秒或每100毫秒都发生一个时间点，我们需要描述状态从一个时间点到下一个时间点的变化方式，因此在一个毫秒或一秒内发生的事情，在离散时间点上考虑行为时，车辆最有可能保持当前的状态，因此这些自反箭头很粗，因为我们想表达最有可能的转换是留在当前状态。我们也可以为箭头设置一些概率，假设我们只使用我们驾驶员的经验和专业知识来推导这些数值，例如，在这种情况下，状态转换的概率为5%，保持相同状态的概率为95%。

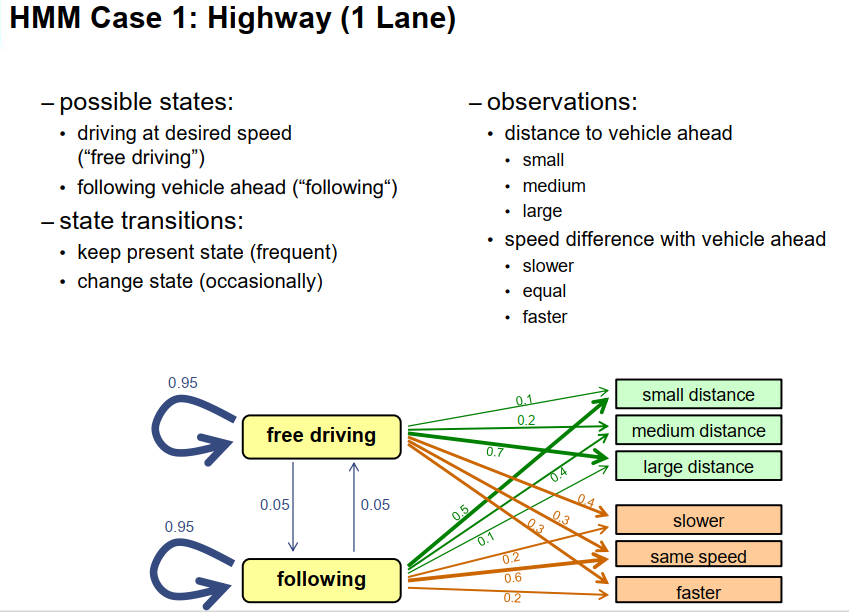
现在让我们谈谈观察结果，例如与前车的距离。我们可以将这个观察结果离散化，不提供以米为单位的数字，而只是说，距离是小的、中等的还是大的，因此我们有三种不同的观察结果或不同的结果，即前车距离的测量可能具有的三种不同结果，对于每一种可能的结果，我们分配一个概率。例如，在这种情况下，我们可以认为如果车辆跟车行驶，那么距离前车很近的概率非常高，因此概率为50%。或者，我们可以表达为，在自由行驶状态下，车辆与前车的距离很大的概率也很高，比如说70%。请注意，箭头的方向表示我们需要建模的是一种条件概率，即在给定某个状态的情况下，观察结果的可能性。我们假设我们知道状态，然后告诉系统，在这种状态下，观察结果是什么样的，而不是反过来。下一个方向是我们接下来要讨论的，我们将讨论如何解决这个问题，但是在行为建模中，我们始终提供概率，即在某个状态下进行某种测量或观察的可能性有多大。

我们还可以引入第二个观察结果，例如与前车的速度差异。在这种情况下，我们还可以将这个观察结果离散化为三种情况，即比前车慢、与前车相同速度或比前车快。同样，我们分配概率来告诉我们在自由行驶状态下，车辆比前车慢的概率有多大。一旦我们建模了这些，我们就可以问如何对车辆的当前状态进行预测或猜测。我们假设我们观察了车辆一段时间，做了一系列的观察，并基于这些观察结果来猜测车辆最可能的状态是什么。

对此，我们实际上想确定的是在给定过去到现在的观察结果的情况下，当前状态的概率。或者，我们想做出预测，即车辆的下一个状态是什么。我们已经在第五章的幻灯片中回答了这些问题，我们已经推导出了一种算法，可以用来迭代计算这些概率。

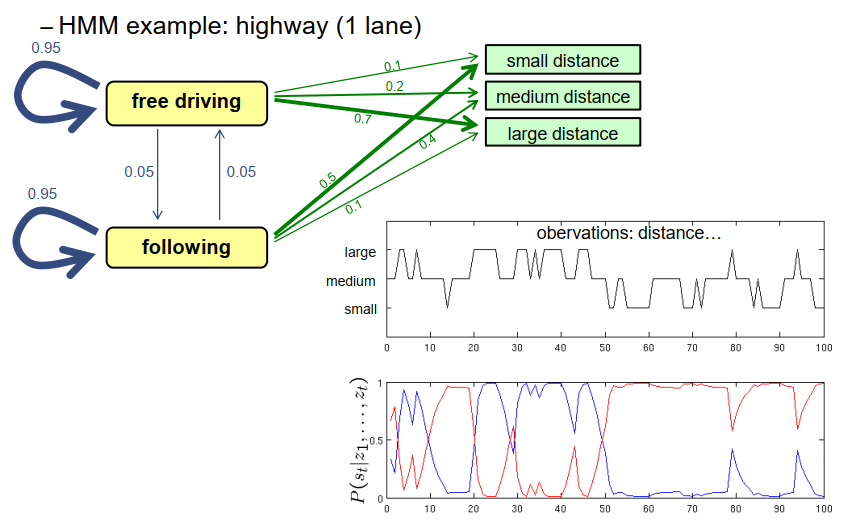
现在让我们看一下对一些人工观察序列应用该算法的结果。左上角显示了隐马尔可夫模型，为了简化可视化，我将其缩减为仅包含单个观察结果，即距离，而且这个距离随时间变化。可以在右下角看到一些图表。上面的图表显示了观察结果的值，它的范围在小、中、大之间，水平轴是时间轴，从时间点0到时间点100。下面的图表显示了考虑到到目前为止的观察结果序列时，在特定时间点上处于某个状态的概率。蓝色曲线是处于自由行驶状态的概率，红色曲线是处于跟车状态的概率。我们可以看到，如果我们观察到较大的距离，那么自由行驶状态的概率显然会更高；如果我们观察到较小的距离，那么跟车状态的概率会更高。我们还可以看到，观察结果与我们的预期有些偏差，但滤波器可以修正这种不精确性。例如，在第50秒到第80秒之间的时间间隔内，车辆大部分时间观察到的距离很小，但在其中的某些时间点，它也观察到了中等大小的距离，但仍然保持跟车状态的概率很大。这意味着这种滤波器可以弥补测量误差和不精确性。

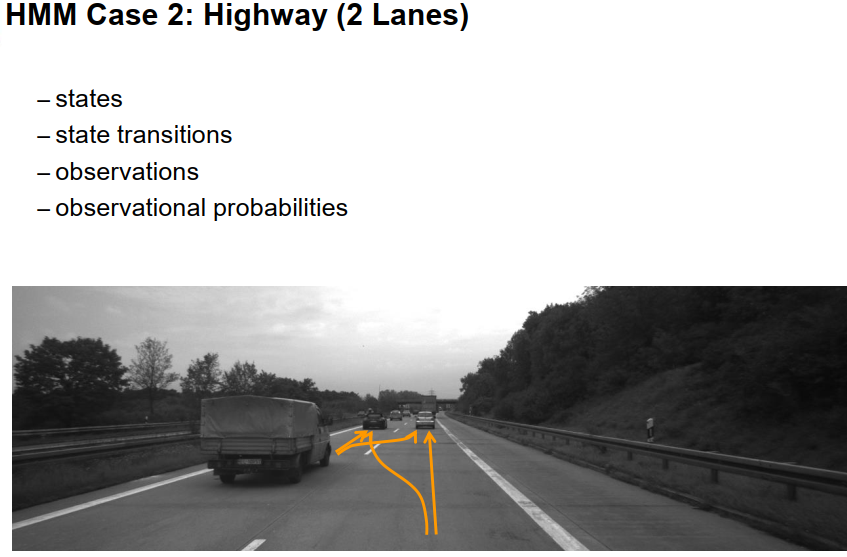
现在让我们将这个任务扩展到具有两个车道的高速公路的情况。在这种情况下，情况当然变得更加复杂，因为我们不能只是跟随前车并处于自由行驶状态，而是可以进行车道变换。因此，让我们讨论我们需要哪些状态、状态转移、观察和观察概率。

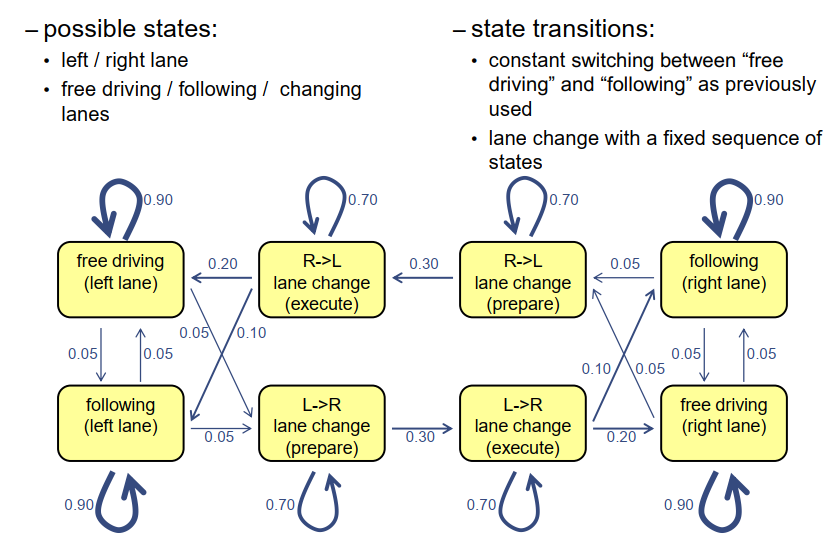
状态必须模拟车辆是在左车道还是右车道上行驶，以及它是自由行驶、跟车还是正在进行车道变换。状态转移模型需要模拟在典型的活动顺序中从自由行驶到跟车的转换，并且还需要模拟车道变换分为准备阶段和执行阶段。为了能够区分它们，将这些车道变换分为两个单独的状态，车道变换准备状态和车道变换执行状态。当然，这些状态存在于从右到左或从左到右的车道变换中，所以总共有八个不同的状态。现在我们可以在图表上放置箭头，显示哪些转换是可能的，哪些是不可能的。当然，在这里我们有一定的自由度来建模情况，所以幻灯片上提供的解决方案是一种可能的建模方法，但也可能有其他适用于这个问题的模型方法。在这里，我使用了单车道高速公路示例中的转换模型，并将其应用于左车道和右车道上的自由行驶到跟车转换，然后添加了一些转换，从跟车或自由行驶状态开始，经过车道变换准备状态，连接到车道变换执行状态，然后转换为另一个车道上的自由行驶或跟车状态。

请注意，我们再次添加了自反箭头，因为当然，最可能的转换仍然是从状态自身到自身的自反转换，否则你将强迫车辆一直更改状态，这在实际交通中是非常不典型的。我们可以为这些转换添加一些数值，暂时使用驾驶员的经验来确定可能的概率。可能的概率如下所示：

此外，我们还必须考虑可能的观察结果。有几个与此相关的观察结果，如横向位置、指示器、前方车辆距离等。当我们检查列表时，我们会发现其中一些观察结果是离散的，如指示器，而其他观察结果则采用实数值，如横向位置或前方车辆距离，通常以米为单位进行测量，因此它们是一些实数。我们需要区分这两种情况。对于离散值，我们需要提供观察概率，对于连续值，我们需要提供概率密度函数来建模状态和观察之间的关系。让我们对一些示例进行建模。

例如，在高速公路驾驶情景中，指示器非常重要，可以区分车道变换和非车道变换。当然，如果我们处于车道变换状态，指示器开启的可能性要高得多，而如果我们处于非车道变换情况下，指示器开启的可能性要小得多。我们可以从指示器得到三种可能的观察结果：指示器关闭、左指示器闪烁或右指示器闪烁。对于我们模型中的八个不同状态（现在用颜色进行编码），我们需要为每个状态中的每个观察结果提供一些概率。这些观察概率在图表中以条形图表示，条形图的高度表示概率。例如，如果我们考虑从右到左车道变换执行状态（深棕色状态），我们可以看到在这种情况下，左指示器闪烁的概率较大，指示器关闭的概率不为零，但很小但不为零，而右指示器闪烁的概率非常小，接近零，可能不是零，但非常接近零。如果考虑左车道上的自由行驶状态（深蓝色状态），我们可以看到在这种情况下，左指示器或右指示器开启的概率都相当小，接近零，而指示器关闭的概率非常大，如此类推。您可以对所有状态进行类似的分析，为每个状态思考在这种状态下指示器关闭、左指示器开启或右指示器开启的可能性有多大。

车辆的横向位置是另一个非常有用的特征。让我们将其建模为一个连续变量。我们可以这样来建模车辆在道路上的横向位置，如图所示。首先，我们考虑车辆所在的车道，然后再考虑车辆在车道上的位置。我们可以通过概率密度函数（例如高斯分布）来建模观测概率。让我们来看一些示例。例如，在右车道跟车状态（浅绿色状态）中，我们预期车辆的横向位置大致位于右车道的中心线附近，并且不会偏离车道的边界太远。因此，我们会在该单元格中放置一个以右车道中心为期望值的高斯分布，并具有一定的标准差，使得在右车道之外的概率非常接近于零。如果考虑从左到右的车道变换执行阶段（深紫色状态），我们当然期望车辆的位置在两个车道的边界之间，也就是在两个车道接触的地方附近。我们可以使用以道路中心线为期望值的高斯分布来建模这种情况，并使用较大的标准差来表示在车道变换阶段，车辆从左向右移动，因此接受更大范围内的位置值。我们可以对每个观测和每个状态进行类似的讨论。

第三点是与前车的时间间隔，这在一定程度上反映了速度和与前车的距离。我们可以说，如果我们处于跟车状态（左车道或右车道），我们预期时间间隔很小，接近于一秒，我们可以在图表中使用高斯密度函数，使其大致以一秒为中心，或者稍微小于或大于一秒，并表示在这些情况下我们预期较小的时间间隔。而在自由行驶状态中，我们预期较大的时间间隔，可以通过以大约三秒为中心、具有较大标准差的高斯密度函数来表示。对于车道变换情况，很难给出具体的测量值，因为我们可能还不清楚车辆在哪条车道上以及可以期望什么样的观测值。如果我们想表达我们对所得到的观测值非常不确定，我们可以在特征空间中放置一个非常宽的高斯分布，以表示我们非常不确定，并且所有的值都是可能的。在这里，使用了这种具有较大标准差的宽高斯分布。

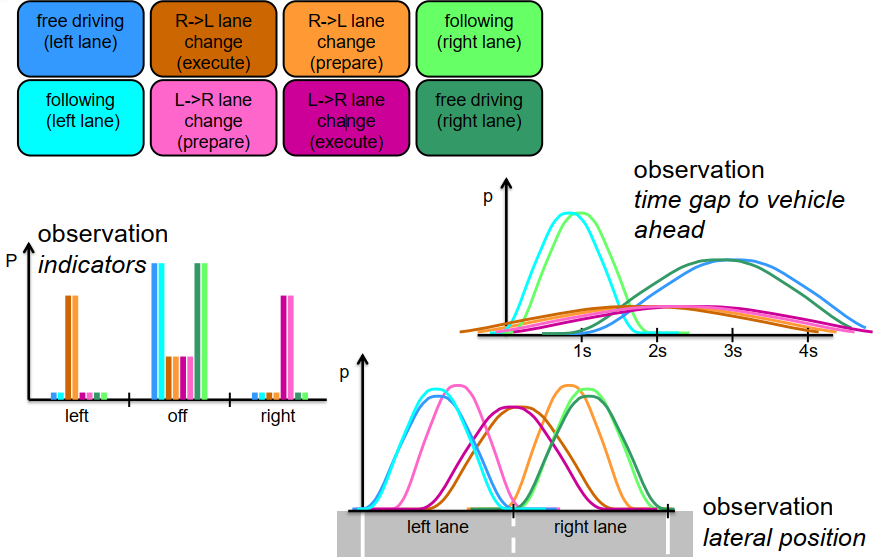
利用隐马尔可夫模型，我们可以测试滤波算法对一些观测序列的性能。下面的例子展示了观测序列，横轴是时间轴，从0秒到50秒，纵轴显示观测值。蓝色线表示指示灯的观测值，值为1表示左转信号灯，值为2表示指示灯关闭。绿色线表示横向位置的测量值，其中0是两个车道接触的位置，正值表示右车道上的位置，负值表示左车道上的位置。在此示例中，我们观察到首先在右车道上的位置，然后从20秒到23秒之间，横向位置发生变化，之后我们观察到负值，即左车道上的位置。

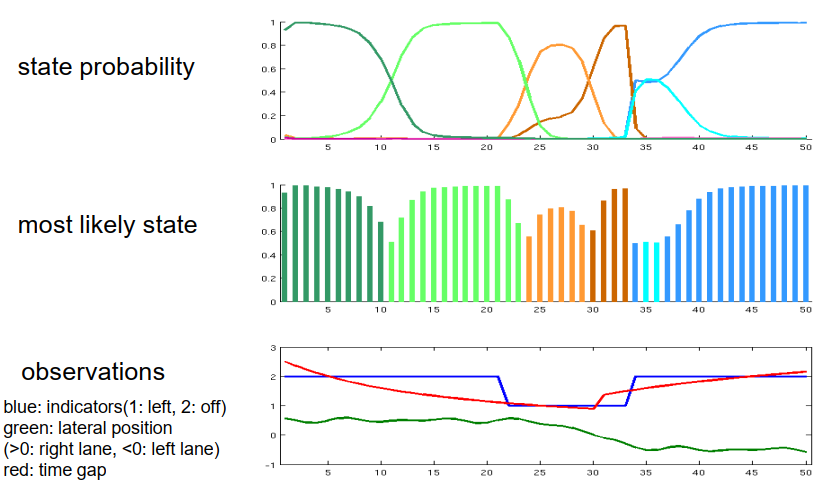
顶部的图表显示了随时间变化的每个八个不同状态的概率。请记住，出于可视化目的，我们对状态进行了颜色编码，因此深绿色表示右车道上的自由行驶状态，浅绿色表示右车道上的跟车状态，以此类推。与之前的颜色编码相同。中间的图表显示了最可能状态的概率，以条形图的形式呈现。我们能看到什么？我们可以看到一系列特定的观测产生了一系列特定的最可能状态。一开始，滤波算法对车辆在右车道上的自由行驶状态非常确定，然后从自由行驶转变为跟车状态。在某一点上，观测提供了一些信息和特征，告诉我们车辆开始执行或准备进行向左车道的车道变换。然后执行车道变换，之后车辆在左车道上行驶。在左车道行驶的开始阶段，算法显然还不确定车辆是自由行驶还是跟车状态，但是一段时间后，车辆自由行驶在左车道上的可能性越来越明显。我们可以看到这个模型是合理的，并且这种序列得出了对车辆状态的良好建模。

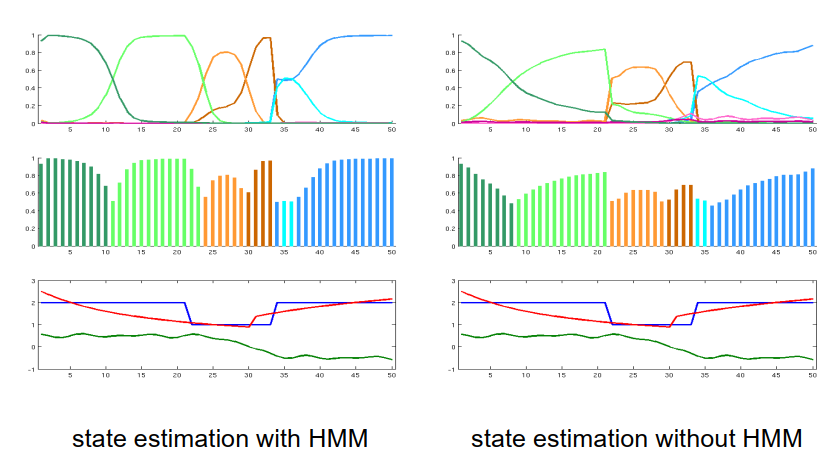
在此将隐马尔可夫模型的状态估计与之前的隐马尔可夫模型进行了比较，左侧部分是前者，右侧部分是后者，后者只使用了观测模型来预测状态，并且移除了状态转移模型，即仅根据单个观测来估计状态。我们可以看到，尽管仍然能够进行一些合理的状态估计，但最可能状态的概率要低于左侧部分，这意味着状态转移概率的使用对稳定整个估计过程非常有帮助。

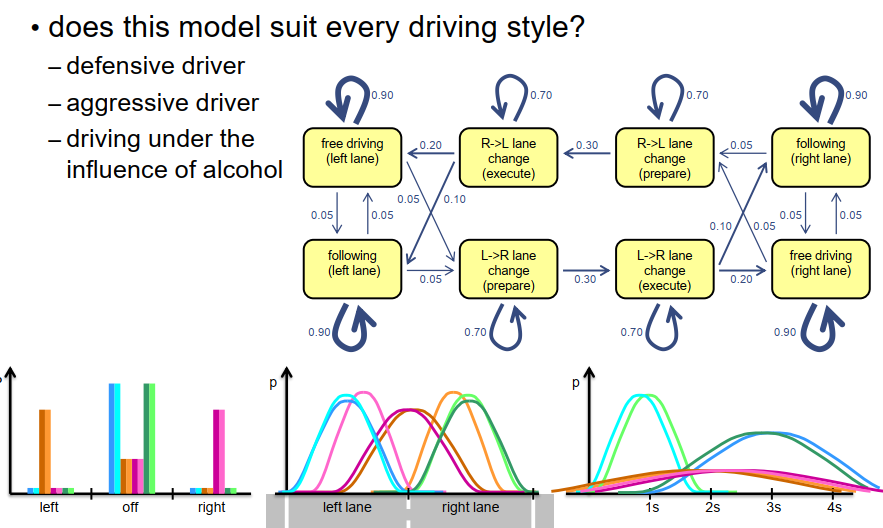
现在我们知道如何估计隐马尔可夫模型的状态以及它在检测车辆或交通参与者当前行为和意图方面的重要性。然而，并非所有驾驶员都以相同的方式驾驶，因此我们可能会面对防御性驾驶员、激进驾驶员，甚至可能会面对那些驾驶方式非常不可预测的驾驶员，例如酒驾的情况。目前我们处理这种情况的方式并没有区分这些不同的驾驶风格。当然，如果我们能猜测到我们面对的是哪种驾驶风格，并且如果我们能针对每种驾驶风格专门化我们的隐马尔可夫模型，那么我们甚至可以提高行为识别的性能。

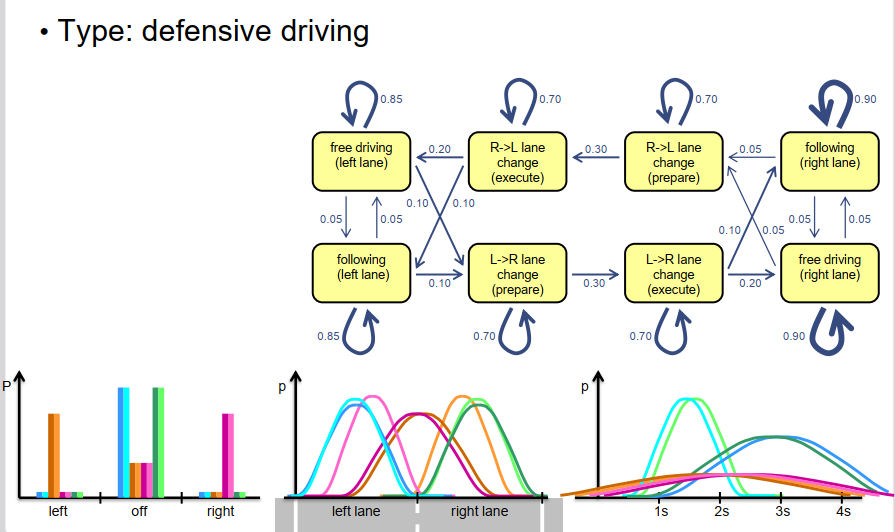
让我们以保守驾驶员为例。我们可以使用相同的基本建模方法和隐马尔可夫模型，并改变一些概率或概率分布，以表达谨慎或小心驾驶员与其他驾驶风格不同的驾驶方式。例如，我们可以认为小心的驾驶员保持与前车更大的距离，因此我们可以稍微将我们预期观察到的时间间隔的密度函数向右移动，这表明这种类型的驾驶员更小心，因此与前方车辆保持更大的时间间隔。我们还可以改变状态转移模型中的概率。例如，小心或保守的驾驶员倾向于更多地行驶在右车道而不是左车道，这意味着我们可以减小模型左车道驾驶状态中保持的概率，增加返回右车道的车道变换概率。

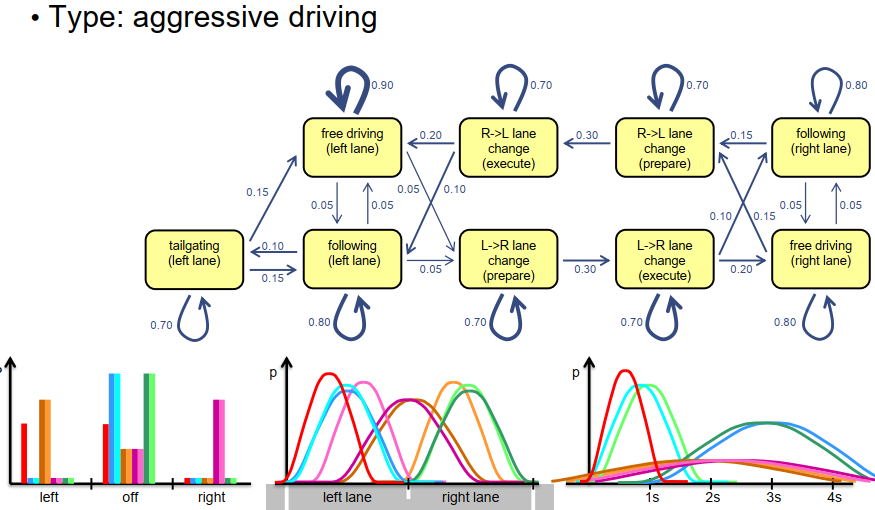
另一种情况是非常激进的驾驶员。当然，在这种情况下，我们也可以改变观测值，减小我们预期的时间间隔，并增加在左车道上行驶的概率，而不是行驶在右车道上。我们甚至可以添加额外的状态，例如紧随其后状态，用于描述在左车道上行驶的驾驶员与前车保持非常小的时间间隔，并试图迫使前车离开左车道。在此情况下，我们添加了第九个状态，紧随其后状态，添加了相应的状态转移概率和一些观测概率。这种类型的驾驶者在现实中是存在的，因此将其建模并不是件坏事。

现在我们已经建立了几种驾驶员类型的模型，当然我们还需要问一下如何找出我们面对的是哪种驾驶员。当然，我们不知道这一点，我们需要猜测或根据我们获得的观察结果进行预测。

答案是我们考虑一些概率，有时称为证据，即在给定某个隐马尔可夫模型的情况下，观察到某个特定的观察序列的概率。如果我们假设我们有两种不同的隐马尔可夫模型，一个用于保守驾驶员，一个用于激进驾驶员，我们可以问：在给定保守驾驶员的隐马尔可夫模型下，观察到某个特定的观察序列的概率有多大？如果我们面对的是激进驾驶员，我们观察到这个序列的概率又有多大？这些就是我们要考虑的概率，但是我们如何计算它们呢？

首先，我们注意到我们可以计算这个证据概率，并将当前状态作为T添加到这些概率中，并保持等式，当然，我们必须添加所有可能的状态St以保持等式，这是边际化规则。接下来，我们可以创建一个增量或递归规则来计算这些概率。首先，我们注意到，St和整个观察序列的概率，给定某个隐藏马尔可夫模型，可以重写为观察到St的概率，给定St和之前的观察值的乘积，再乘以给定隐藏马尔可夫模型的St-1和之前的观察值的概率。这仅仅是条件概率的定义。然后，我们可以利用隐马尔可夫模型的随机独立性属性来简化概率，因为我们知道在某个状态下观察到某个观察值的概率与先前的观察值无关，所以我们可以在条件概率的条件部分忽略那些先前的观察值。

在方程的下一行，我们将St的概率分解为给定St-1和截至时间T-1的所有观察值的条件概率和边际概率。我们可以再次利用隐马尔可夫模型的随机独立性属性来简化概率，因为我们知道从状态St-1转换到状态St不依赖于先前的观察值，我们可以简化这个术语，并得到一个简单的状态转移概率。现在，我们到达了这些变换序列的末尾，我们看到在这些方程的左边，我们计算的是到时间T为止的这种概率，而在底部的最右边，我们计算的是到时间T-1为止的这种概率，唯一的区别是在方程的左边，这种概率是到时间T的一种类型，而在最右边，则是到时间T-1的一种类型。因此，我们得到了一种迭代规则，我们可以从一个时间点逐渐增加这种概率，另外两种概率只是观察概率和状态转移概率，这些概率在我们的状态转移图中已经进行了建模。

因此，我们可以看到，我们要计算的这种概率（左边）直到时间点T，可以表示为观察概率、一些转移概率和我们要计算的同一种概率（但是针对前一个时间点）的组合。如果我们从时间点T到时间点0开始递增猜测这种概率，那么我们可以在程序中实现并反复执行这个公式。在这个算法的每个周期中，我们添加另一个观察值，通过这样做，我们可以计算长序列的整个过程。

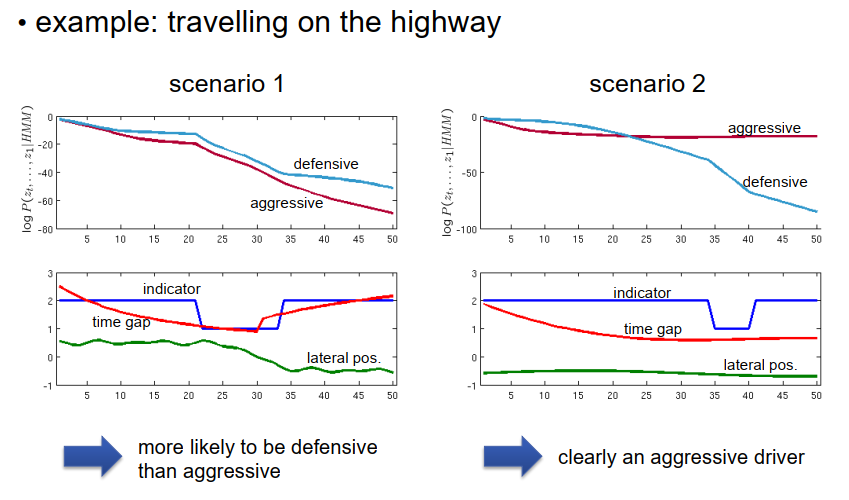
在这里，我们可以看到这个算法计算证据的性能，用于两个模型：激进驾驶员和保守驾驶员模型在底部，我们再次看到观察值，实际上是我们之前考虑的同一组观察值。在上面，我们看到了保守驾驶员和激进驾驶员的证据的对数。它显示为对数形式，因为证据本身变得非常非常小，非常接近于零，如果在这个图上，它将不再可见，几乎等于零，但是如果我们取对数，就变得更清晰，我们可以清楚地区分哪个模型有更大的证据。我们可以看到，在开始时，两个模型的证据几乎相同，但是后来变得清楚，我们更有可能面对的是保守驾驶员而不是激进驾驶员。

让我们稍微改变这个情景，改变观察值，这里是另一组观察值，车辆始终在左车道上行驶，时间间隔变得非常短，在左车道上左侧的指示灯亮起。在这里，我们可以看到两个模型的证据。开始时，保守驾驶员模型似乎更有前景，但是当时间间隔变小，特别是当左车道上的指示灯亮起时，很明显我们面对的是一个激进的驾驶员而不是保守的驾驶员。

这些是使用隐马尔可夫模型进行行为识别的一些基本方法，但是当然，这些并不是我们可以使用隐马尔可夫模型解决的所有任务。有时我们需要计算最合理的状态序列，而不仅仅是考虑在某一时间点上最可能的状态，然后在下一个时间点上的最可能的状态是什么。这意味着我们要寻找最大化给定所有观察值的所有状态的概率的状态序列S1到St。有一个算法可以解决这个任务，它与前向算法有一定的关联，但计算稍微复杂一些，它被称为维特比算法，由于时间有限，我们这里不介绍它，但值得知道有这样一个算法，如果需要的话，可以在文献中查找。

另一个问题是如何设置转移概率和观察概率在我们的模型中。到目前为止，我们认为我们在驾驶中有一些人为的专业知识，因此我们可以设置一些至少合理的概率。然而，这可能不是最优的方法，有一个算法可以为您完成这项工作，它被称为鲍姆-韦尔奇算法。鲍姆-韦尔奇算法使用许多示例序列以及隐藏马尔可夫模型的基本结构（即包含所有状态和可能的转移的结构）来估计转移概率和观察概率。然而，它不能从头开始估计这些概率，所以即使对于鲍姆-韦尔奇算法，我们也需要一些合理的模型作为算法的初始化，然后鲍姆-韦尔奇算法可以在一定程度上优化转移概率和观察概率。

让我们用 Jonas Fill 在他的博士论文中使用马尔可夫模型来对车辆行为进行的建模总结本章内容。他的目标是识别短视频序列中的驾驶行为，他区分了四种不同的行为或驾驶动作，分别是超车、并行行驶、跟随其他车辆和自由行驶。超车和并行行驶有什么区别呢？在这里，所谓的并行行驶是指车辆已经在可以超越另一辆车的车道上，并且保持在该车道上，在不进行任何车道变更的情况下超越另一辆车，而超车则意味着车辆进行车道变更以超越另一辆车。

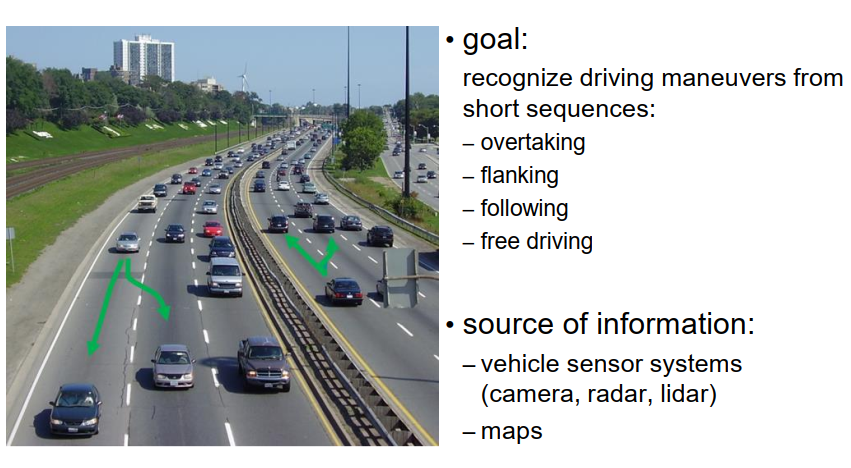
在他的工作中，信息来源包括车辆传感器系统（相机和激光雷达传感器）和可用于模拟车道的地图，从而将不同的车辆分配到不同的车道。他采用的方法是为每种驾驶动作使用一个隐马尔可夫模型，然后计算每个模型的证据，并根据证据返回一些描述在特定情况下某种驾驶动作的概率。

他采集的观测数据主要是两辆车之间的距离（横向和纵向距离）、速度差异和加速度差异。由于他可以直接从车辆传感器中获得速度差异，并且加速度差异是由速度差异派生出来的。

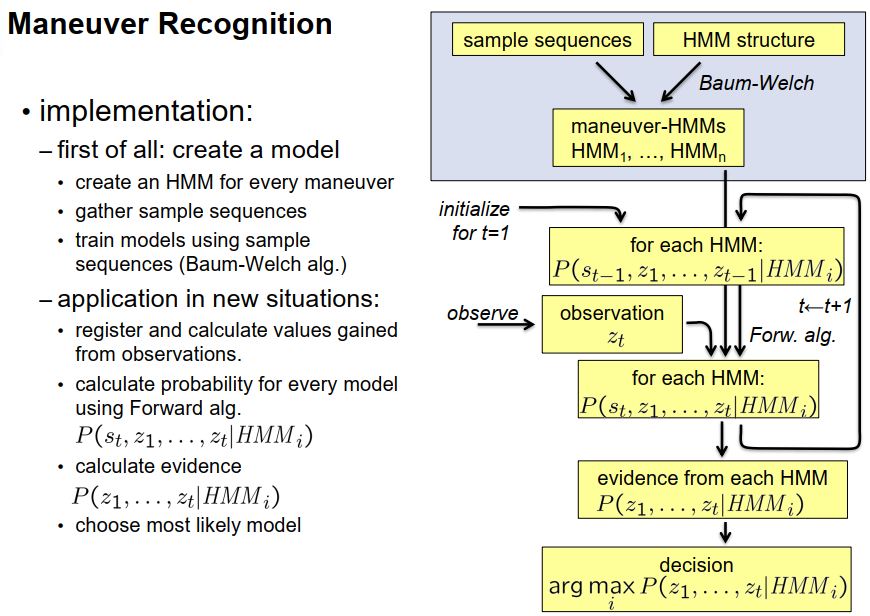
那么他是如何实现的呢？首先，他需要创建一个隐马尔可夫模型，为每个驾驶动作创建一个模型结构。他收集了大量的示例数据，然后使用鲍姆-韦尔奇算法来优化每个隐马尔可夫模型的转移和观测概率。完成了这个步骤后，他可以使用这些训练好的模型来预测其他车辆的行为。预测的过程如下：对于观察到的每一种情况和每一对车辆，他都会为时间点1初始化每个隐马尔可夫模型，然后进行一次观测或一组观测，基于此使用前向算法计算一次迭代。然后，他可以回到上面的点，将时间增加一个时间点，并继续进行下去。他以增量、迭代的方式使用前向算法。同时，他还可以计算每个隐马尔可夫模型的证据，通过整合当前状态来实现。

基于此，他可以确定当前最可能的隐马尔可夫模型，即最可能的驾驶动作。

一个例子，这是在一个测试区域上记录的一个示例视频，视频中有三辆车。我们可以在视频中看到的两辆车在测试区域上行驶，第三辆车是装备有相机和传感器的自动驾驶车辆，观察这两辆车辆。现在，当开始播放视频时，将在左侧看到用于提取特征的视频，在右侧将看到一个绘图，显示了超车、跟随和并行行驶这三种驾驶动作的概率，或者更准确地说，归一化的证据。在开始时，两辆车大致上是相互跟随的，因此跟随和超车的证据较大，而并行行驶的概率较低。现在我们看到一辆车进行了车道变更，现在我们更多地处于并行行驶或超车的情况，车道变更后，我们可以看到超车行为仍然存在，所以我们知道我们观察到的行为非常可能是一种超车行为。

现在我们可以总结整个章节的内容。我们介绍了马尔可夫模型用于行为建模，状态用于建模车辆的不同行为模式，状态转移描述这些行为模式之间的可能顺序，观测模型描述了我们可以进行的测量，并描述了这些测量在不同情况下的出现情况。由于隐马尔可夫模型是一种随机系统，它能够通过概率来描述所有的不确定性，这是一个很大的优势。当然，我们也看到了如何使用这些隐马尔可夫模型来对高速公路上的驾驶行为进行建模。

然后，我们看到通过这种模型我们可以进行行为识别，即估计最可能的状态的算法，并且这些算法基于经典的预测和创新步骤，在第五章中已经介绍过。

除此之外，我们还介绍了一种新的算法，前向算法，通过它可以计算不同模型的证据，并通过比较这些模型来确定哪个模型最能解释数据。

这是关于行为识别的第八章的结尾了。希望你对内容感兴趣，并可能去阅读本章所引用的文献的兴趣。此外，这也是最后一章。