Chapter 5 Tracking Moving Objects 追踪移动物体

欢迎来到《汽车视觉》课程中关于跟踪运动物体的第五章。在本章中，我们将讨论如何利用相机、激光雷达传感器或其他环境传感器来估计场景中物体的运动。与像素级方法不同，我们将把注意力转移到物体级别上。这意味着我们假设环境中的物体已经被检测出来，并且我们能够确定它们的三维位置。

我们想要估计的运动是物体的三维运动，而不仅仅是二维的光流向量。在本章中，我们将探讨各种物体跟踪技术。以下是与本章相关的专业文献列表：

• Greg Welch and Gary Bishop, An Introduction to the Kalman Filter, Technical Report University of North Carolina at Chapel Hill, 1995 (http://www.cs.unc.edu/~welch/kalman/)
• Simon J. Julier, Jeffrey K. Uhlmann, Hugh F. Durrant-Whyte, A new approach for filtering nonlinear systems. Proceedings American Control Conference, 1995, pp. 1628-1632
• Sebastian Thrun, Wolfram Burgard, Dieter Fox, Probabilistic Robotics. MIT Press, 2005, Chapters 2-4
• Arthur Gelb, Applied optimal estimation. M.I.T. Press, 2006.
• Yaakov Bar-Shalom, X. Rong Li, Thiagalingam Kirubarajan: Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software. Wiley, 2001

Motion Estimation by Regression 通过回归进行运动估计

现在，让我们从一个在文献中通常没有明确提到但在实践中仍然相关和有用的物体跟踪简单方法开始：回归运动估计。

在这个估计问题中，我们在不同的时间点观察到一个物体，并以一定的准确度知道它的位置。我们的目标是尽可能准确地估计物体的精确位置、速度甚至加速度。速度包括运动的速度和方向。

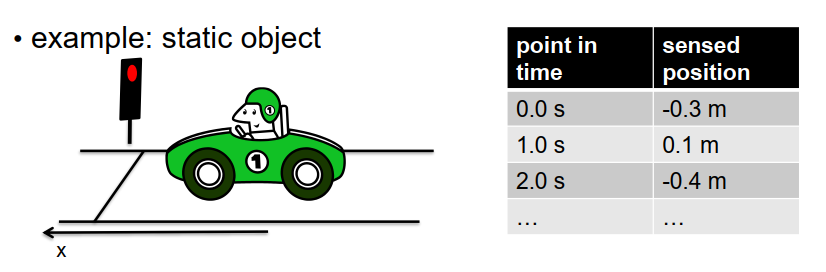
让我们从一个简单的例子开始。假设我们观察到在红灯前等待的汽车。我们在不同的时间点进行多次测量，得到表示车辆X位置的一维测量结果。由于测量噪声，这些测量结果会有变化，就像例子中展示的那样。

为了估计车辆的准确位置并消除测量结果中的随机变化，我们可以对测量结果进行平均。通过计算所得测量结果的均值，我们可以估计一个更可靠的车辆位置。我们还可以估计测量结果的方差，这提供了我们知识的不确定性或扩散的指示。

回归

这种平均技术是基本而直观的，大多数人都会自然地使用它。现在，让我们思考是否可以将这种技术扩展到车辆开始移动的情况。

在第二种情况中，假设我们观察到一辆以恒定速度移动的车辆。同样，我们在不同的时间点上获取了车辆位置的多次测量结果，如表格所示。我们的目标仍然是尽可能准确地估计车辆的位置和速度，考虑到测量过程中的随机误差。

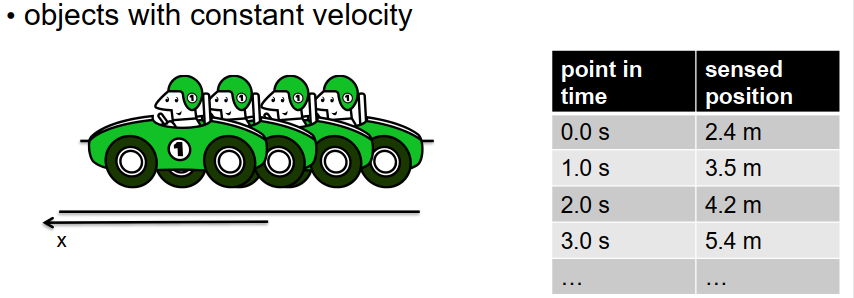
• 假设：匀速行驶

• 寻找最适合测量的$x_0$和$v$。

测量结果与真实位置相似但并不完全相同。以与之前类似的方式，我们可以建立一个运动模型。如果我们假设恒定速度，我们可以将时间T的测量位置表示为初始位置x₀加上未知速度V乘以时间t的积分。然而，测量结果受到额外噪声的影响。

现在，我们的目标是以最佳方式找到运动模型的未知参数，即x₀和V，以使它们最好地适应我们获得的测量结果。我们可以将其制定为优化问题。对于给定的速度V和初始位置x₀，我们计算根据运动模型预期位置与测量得到的位置Xᵢ之间的差异。我们对每个差异进行平方，将它们在所有测量结果上求和，并通过优化x₀和V来最小化这个总和。我们可以通过计算对于x₀和V的总和的偏导数，然后解决得到的方程组来实现这一目标。

这一步并不特别困难。您可以在家用纸张尝试一下。得到的方程将如下所示：

最小化问题可以通过将导数（就$x_0$和$v$而言）设为零而得到解决。

$\rightarrow$ linear regression:

这被称为线性回归，只要左侧的矩阵具有满秩，您就可以解决这个线性方程组以找到唯一的解，而这通常在您至少拥有两个车辆测量时可以实现。

使用这种方法，您可以轻松地得出x₀和V的估计值。此外，您还可以得出x₀和V的方差，以评估估计值的质量。您可以对车辆在未来时间T的位置进行预测，甚至计算该预测的方差以确定其可靠性。

现在让我们扩展这种方法。假设车辆从交通灯开始，在灯变绿时，车辆加速。假设车辆处于固定位置或以恒定速度移动已不再有效。因此，我们需要通过引入加速度项来增强运动模型。具有恒定加速度的加速运动的运动模型如下：

X(t) = x₀ + V₀t + (1/2)at²

同样，我们需要考虑到我们的测量结果受到噪声的影响，因此时间T的感知位置与运动模型中的项并不完全匹配。

我们可以按照类似于之前的过程，并创建一个优化问题，在其中最小化随时间变化的感知位置与基于运动模型的预期位置之间的误差。使用类似于恒定速度情况的技术，我们可以推导出一个线性方程组，并解决它以获得x₀、V₀和a的有效估计值，分别表示位置、速度和加速度。这个案例也是线性回归的一个示例。

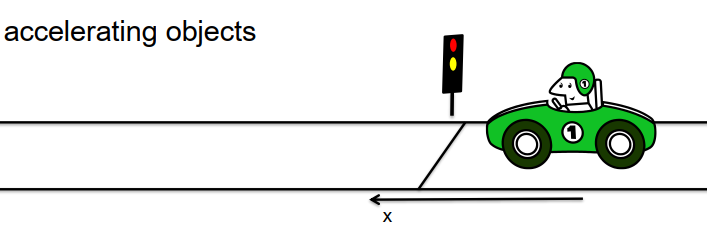
• 假设：恒定加速度

• 寻找最适合测量的$x_0、v$和$a$。

$\rightarrow$ linear regression

正如我们所见，回归方法在许多方面优于其他方法。它们使用简单且计算高效。根据我的经验，它们非常适用于许多对象跟踪和运动估计任务。只要运动模型在未知参数上呈线性依赖，回归可以用于估计一维、二维甚至三维的直线运动。我鼓励您在面对运动估计任务时尝试使用回归方法，看看它是否提供了令人满意的解决方案。本章介绍的其他方法，如卡尔曼滤波器或粒子滤波器，使用起来更加复杂。因此，我的初步建议始终是探索回归方法。

当然，回归方法也有局限性。在处理可以通过解析方法求解的直线运动时，它们效果良好。然而，在处理曲线轨迹时，情况变得更加具有挑战性。通常，我们会遇到无法通过解析方法解决的优化问题，需要使用数值求解器。与通过解析方法解决系统相比，这可能会降低效率。

Example

现在，让我们看看如何通过一个来自机器人足球领域的示例成功应用回归方法。图片显示了两支配备有摄像机的自主机器人队伍，这些摄像机提供了对环境的全方位视图。球，为了便于识别，被涂成橙色，它在比赛中扮演着核心角色。准确估计球的运动对于机器人做出明智的决策至关重要。

我们的方法基于这样一个假设：将球的位置投影到地面时，我们通常观察到具有恒定速度和方向的运动。尽管由于弹跳、碰撞以及被机器人踢动或带球等原因，这个假设并不总是准确的，但在短时间内（大约200-300毫秒）是成立的。在垂直方向上，由于重力的影响，运动是不同的，因此我们建模了一个具有已知因子（重力）的加速运动。此外，我们考虑了球的偏转和与地面的碰撞。通过将这些因素纳入运动模型，我们将任务视为一个回归问题。

我们使用了3到15个观测值，每33毫秒进行一次观测，从而得到总的观测时间范围从67毫秒到500毫秒不等。我们根据球的偏转、踢球或与物体碰撞来调整观测时间。如果观察到这些现象，我们将观测长度减少到三个观测值。当运动可以准确地建模为具有恒定速度的直线运动时，我们逐渐增加观测数量，最多达到15个。通过应用讲座中介绍的回归方法并进行一些调整，我们成功地获得了球的速度估计值。

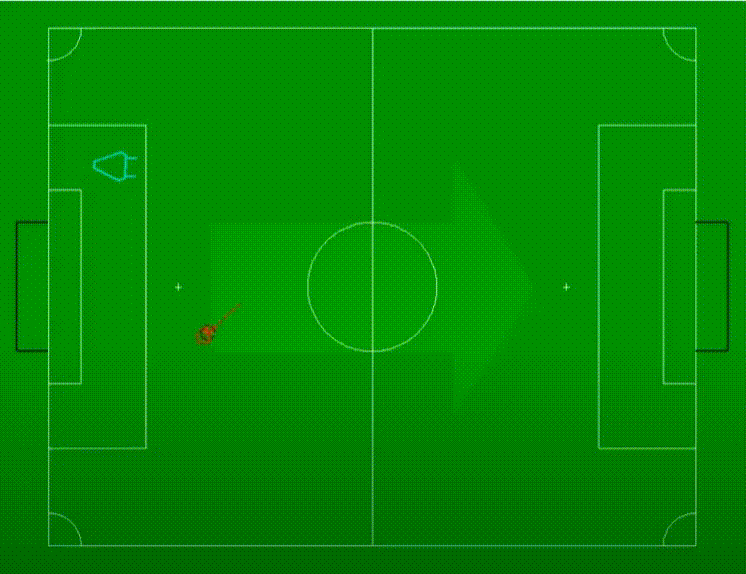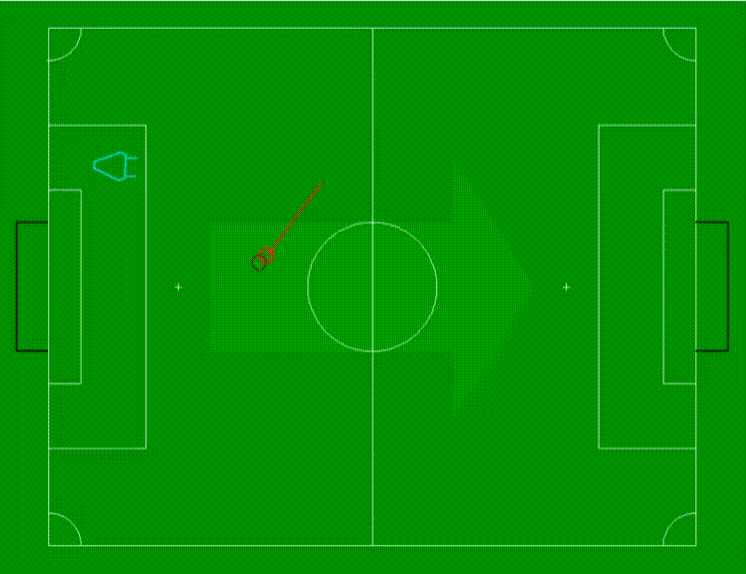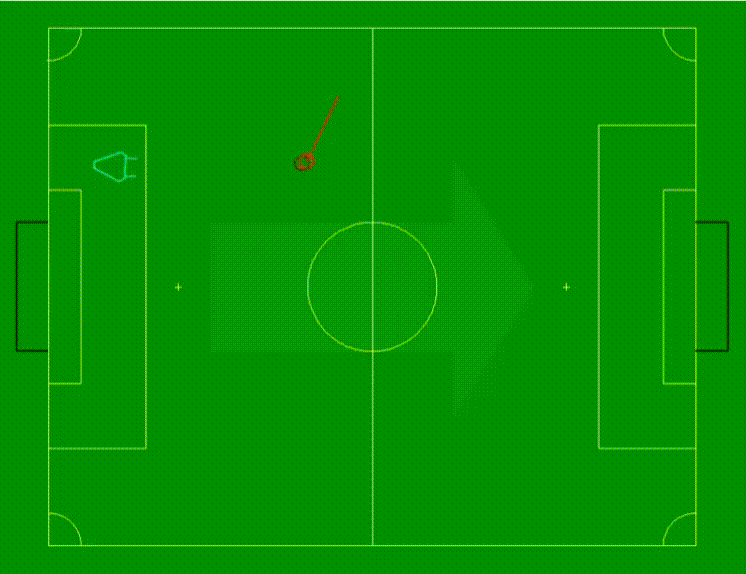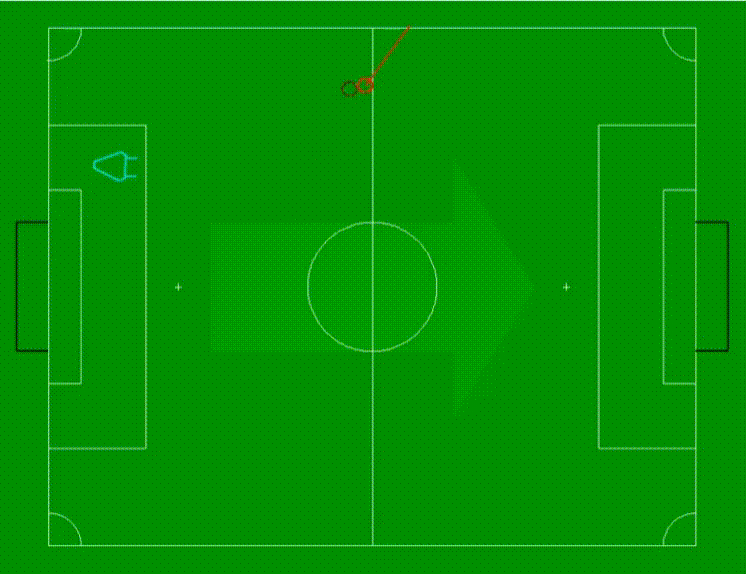
让我们来看看这种方法在我们实验室进行的一项实验中的表现。在实验中，一个机器人被放置在左侧的某个位置（用青色三角形表示），而一个球从右向左滚动到机器人前面。

球的感知位置用深红色虚线圆圈表示，而使用回归方法估计的球位置则用浅红色圆圈表示。从浅红色圆圈中心开始的线表示球的估计运动方向和速度。线越长表示球的移动速度越快。

视频以俯视图展示了情景，并以循环方式播放，球始终从底部滚动到顶部，然后再次从底部开始。在前两个循环中，没有估计到球的位置，因为我们只有两个观测值，而对于第一个估计，我们需要至少三个观测值。然而，在此之后我们获得了有效的位置和运动估计。需要注意的是，由于设置的低分辨率，对球的三维位置估计的精度有限。尽管如此，我们还是成功地得到了球的位置和速度的令人满意的估计。

在比赛场景中，观测机器人也在运动中，我们需要考虑机器人的自我运动并在估计球的位置之前对其进行补偿。这个估计必须在与足球场固定坐标系中进行，而不是机器人坐标系。否则，球的速度估计中可能出现人工的伪影。

当时，这种方法被证明非常成功，我们是足球机器人联赛中的顶级团队。这意味着我们对球的运动估计是相当准确的。

Basic of Probability Theory 概率论基础

在我们深入研究其他对象跟踪技术之前，让我们简要回顾一些概率论的基础知识。概率论涉及随机事件，这些事件偶尔发生但并非总是发生。事件的概率表示其发生频率。如果一个事件总是发生，其概率为一；如果从不发生，则概率为零。概率用大写字母 “P” 表示，例如 P(A) 表示事件 A 的概率。

当多个事件同时发生时，我们可以定义联合概率来确定所有这些事件同时发生的频率。另一方面，条件概率涉及多个事件，并询问在事件 B 已经发生的情况下事件 A 发生的频率。

为了理解这些概率类型之间的关系，我们引入随机变量。随机变量可以被视为在随机过程中取值的变量。有两种类型：离散随机变量，其具有有限或可数的值集（例如计算自行车的数量），以及连续随机变量，它可以取任何实数值（例如测量车辆的速度）。

对于离散随机变量，随机事件对应于随机变量具有特定值或落在某些范围内。对这些事件分配概率是直接的。然而，对于连续随机变量，随机事件是使用区间来定义的。例如，一个事件可能涉及变量落在特定区间内或区间的并集内。对于连续随机变量，只能使用区间来定义随机事件。

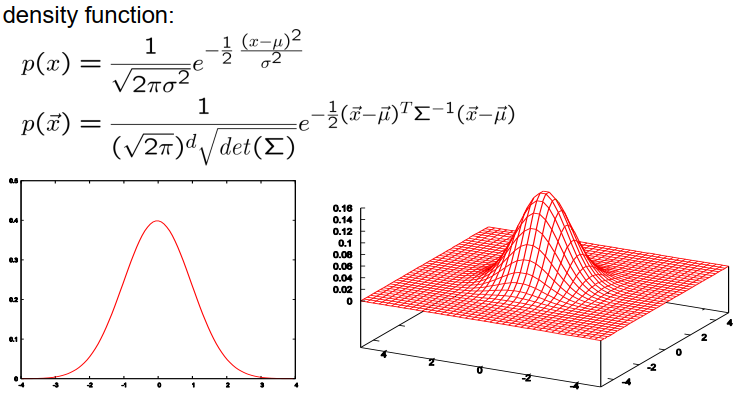
高斯分布

Hidden Markov Models 隐马尔科夫模型

让我们继续学习关于对象跟踪的章节，并介绍一种称为隐马尔可夫模型（Hidden Markov Models，HMMs）的对象行为概率模型。HMMs的主要思想是我们假设我们要观察的对象可以通过状态和随时间变化的状态序列来描述。

为了实现这一点，我们的目标是创建一个概率模型，可以描述系统处于某个特定状态的可能性，以及在该状态下观察到特定观测的可能性，以及从一个状态转换到另一个状态的可能性。让我们考虑一个简单的例子，观察一个以恒定速度行驶的汽车。

在这个例子中，我们可以使用两个变量来描述系统：汽车的当前位置和当前速度。我们可以将这些变量总结为一个向量，并将系统状态定义为这两个变量的组合。一旦我们知道了状态，我们还可以定义一个转移模型。例如，如果车辆在时间t处于某个位置并以某个速度行驶，那么在时间t + Delta时，它将位于某个后继位置，可以计算为旧位置加上Delta乘以当前速度。后继速度将与当前速度相同。在这种情况下，我们可以将一步之后的状态与当前状态之间的关系表示为矩阵-向量乘法。

然而，现实世界中的系统并不完美，通常会偏离确定性行为。我们可以通过在状态转移函数中添加一个随机噪声项来对优化行为的随机偏差进行建模。这个噪声项代表小的随机数，考虑到系统与优化行为的偏差。

此外，我们假设我们可以使用传感器来观察系统。这些传感器测量与系统当前状态相关的某些物理变量，尽管它们可能不直接测量状态本身，这可能是具有挑战性的。例如，如果我们有一个观察场景的摄像机，我们可以测量车辆的位置。这允许我们建立状态与位置之间的映射，将位置视为观测。在测量过程中，我们还考虑了一些测量噪声，它会干扰测量结果。通常，测量值接近实际位置但并非完全相同。这种测量不准确性可以通过添加一个加性噪声项来建模，这是一个接近零的小随机变量。如果系统的状态由包含汽车位置和速度的向量描述，我们可以将观测表示为车辆位置加上一小部分噪声。这也可以用矩阵-向量表示法表示。

• example: car with constant velocity - system state: position, velocity

• transition:

• system state is not directly observable
• observations: every state produces an observation

• example: camera observing a car.
• system state

this is interesting for us, but it cannot be observed

• velocity is not observable
• position can be observed up to small random errors

this can be observed

此时，重要的是要理解我们的主要兴趣在于估计系统的状态。我们想要估计车辆的位置和速度，但我们无法直接测量状态。相反，我们可以测量观测值。因此，具有挑战性的任务是在给定一系列观测的情况下推导出状态。

现在让我们正式介绍隐马尔可夫模型（Hidden Markov Model，HMM）。隐马尔可夫模型是一个离散时间的随机状态转移系统，其中观测和后继状态完全依赖于当前状态，而不依赖于先前的状态或观测。

数学上，这个特性通过下面的两个公式描述，但让我们逐步解释定义。首先，HMM是一个状态转移系统，正如我们所见。我们使用当前状态来描述系统，并假设当前状态与下一个状态之间存在随机关系。这些关系为系统引入了随机性，使其成为随机的。系统是离散时间的，这意味着我们只关注系统在特定时间点的状态，例如每秒一次，不考虑其之间发生的情况。

定义还说明观测和后继状态完全依赖于当前状态，而不依赖于先前的数据或观测。这个假设被称为随机独立性。它意味着如果我们知道当前状态，我们就拥有了预测系统未来行为和提供的观测的所需信息。对历史、先前状态和观测的了解对确定未来行为没有贡献。这种独立性假设允许我们简化所涉及的条件概率。

A Hidden Markov Model (HMM) is a time-discrete, stochastic state transitioning system. Its observation and its successor state depend entirely on its present state and do not depend on previous states or observations.

当使用HMM对世界进行建模时，我们希望根据一系列观测来确定当前状态。虽然我们无法精确知道随机系统中的当前状态，但我们的目标是估计最可能的状态及其概率。我们想要计算给定迄今为止所有观测的条件下的当前状态的概率。

相关的任务是预测，我们希望预测系统未来一步的状态。给定时间t的观测，我们想要进行预测并估计最可能的未来状态及其概率。这两个问题是相互关联的，可以同时计算。幻灯片中展示了它们之间的关系，通过公式表示。

第三行中出现的状态转移概率表示系统从状态St转移到状态St+1的概率。在使用HMM对世界进行建模时，我们需要提供这个转移概率。第二行中的第二项表示给定到该时间点为止的所有观测的概率。这个概率是从上方的方程中导出的，其中我们使用贝叶斯规则重新排列了术语。通过这样做，将St给定到时间T-1的观测的概率乘以分子，并添加了一个分母，其中包含给定所有先前观测的St到时间T的概率。

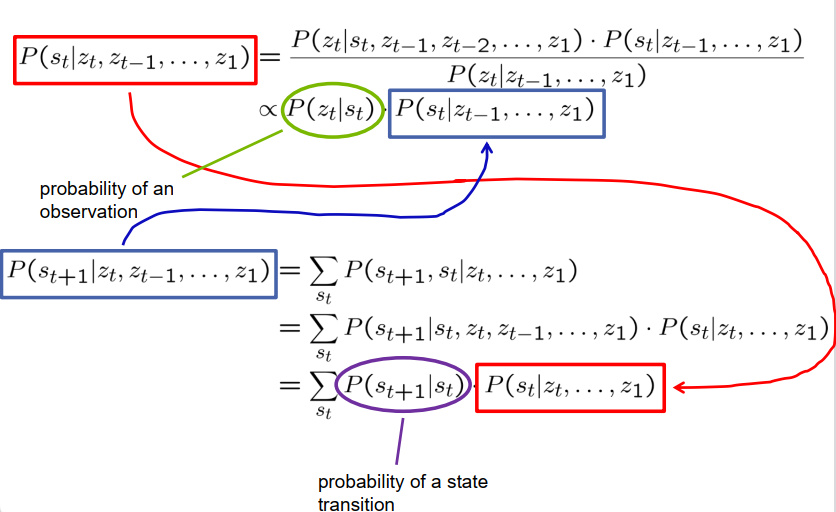
现在我们可以观察到分子中的第一项具有一个形式，我们可以应用随机独立性的假设。它表示给定状态和一些先前观测的情况下观测的概率。根据HMM中的随机独立性假设，我们可以从该项中删除先前的观测，从而显著简化了分子。

分母包含一个与当前状态完全独立的项。它表示获得这些观测的概率。由于它不依赖于当前状态，可以将其视为一个常数，与当前状态无关。由于我们对当前状态的概率感兴趣，这个项作为一个归一化因子。我们可以在符号∝（与之成比例）中隐藏它，如公式的第二行所示。在第二行中，第一项表示作出某个观测的概率。这一方面描述了传感器和测量过程。例如，如果一个车辆位于某个位置，并且我们有一个观测它的摄像头，这个项表示观测到该车辆的特定观测的可能性。这是隐马尔可夫模型中的常见建模方面。

第二项具有一种概率形式，它使我们能够根据先前时间T-1的所有观测对时间t的状态进行预测。它表示左侧幻灯片的第二部分涉及的概率。然而，我们可以观察到这两个项之间的索引已经增加了。这表示我们在第一项的计算中使用了第二部分的计算结果作为输入。这两个步骤之间的时间发生了演化。

这引导了一个基于迭代过程的基本思想，用于逐步估计给定观测序列的系统概率。它由两个步骤组成，即预测步骤和创新或校正步骤。

在预测步骤中，我们计算预测状态概率，即给定时间T的观测序列的情况下的St+1的概率。这个步骤允许我们对系统的下一个状态进行预测。 在创新或校正步骤中，我们采用在时间T+1处的新观测，将在预测步骤中计算的概率纳入其中，并计算给定所有观测的时间T+1的状态概率，包括时间T+1的观测。这个步骤将新的测量结果纳入，并将其整合到我们对系统状态的了解中。

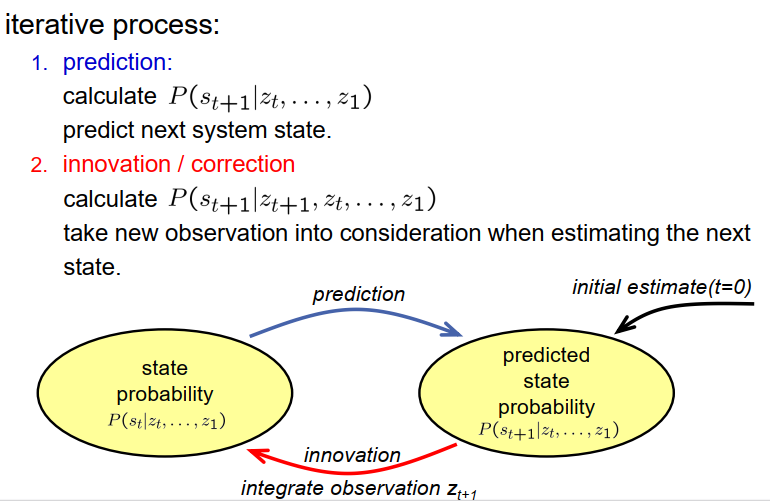
如图所示，整个过程从预测状态概率的初始估计开始。然后，我们融入一个测量并计算状态概率。我们通过在预测和创新步骤之间交替进行，进行预测、融合测量并更新对系统状态的了解，重复这个过程。

这个迭代过程使我们能够根据观测序列逐步估计系统的概率，考虑到系统的动态性和新的可用测量。

这个过程可以逐步进行说明。我们从计算在没有任何观测的情况下处于状态S1的概率开始。我们对这个概率做出一个初始猜测。然后，我们融入一个测量并计算在给定观测Z1的情况下处于S1的概率。接下来，我们进行预测步骤，计算在给定Z1的情况下处于S2的概率。然后，我们执行另一个创新步骤，计算在给定Z2和Z1的情况下处于S2的概率。我们继续进行预测步骤，计算在给定Z2和Z1的情况下处于S3的概率。随后，我们进行创新步骤，将新的测量Z3纳入计算。这个过程继续进行，对每个后续的时间点进行预测和创新步骤，例如预测时间4的状态并融入时间4的测量。这个迭代过程重复进行，根据可用的观测估计状态概率。

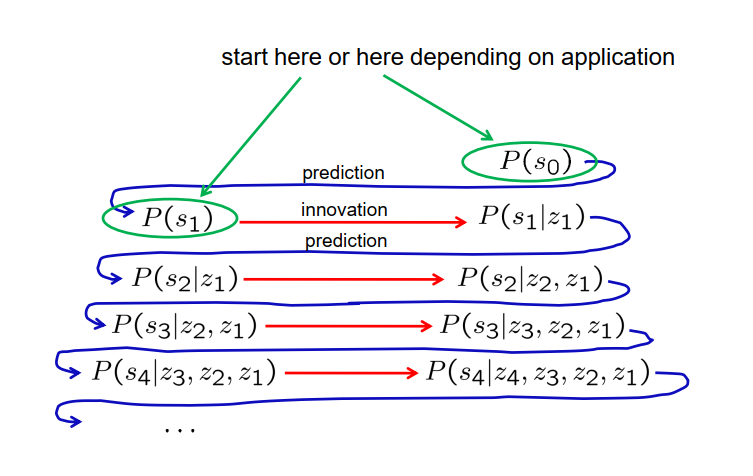
值得一提的是，并不总是必须从创新步骤开始。根据应用的不同，我们也可以从预测步骤开始。例如，我们的初始猜测可以是在没有任何观测的情况下时间0的初始状态的概率。然后，我们可以通过预测步骤启动过程，计算在没有任何观测的情况下处于状态1的概率。选择从预测或创新步骤开始取决于具体的场景和最合适的方法。

在隐马尔可夫模型中使用预测和创新步骤来估计状态概率的基本思想是优雅的。然而，在实践中，评估这些推导出的方程有时可能具有挑战性。但在特殊情况下，例如处理具有有限状态和观测数量的离散状态变量和离散观测时，可以将隐马尔可夫模型表示为图形，并在表中组织概率。

• 特殊情况：
  • 有限数量的可能状态和观察
  • 过渡和观察概率可以用图和/或表来表示

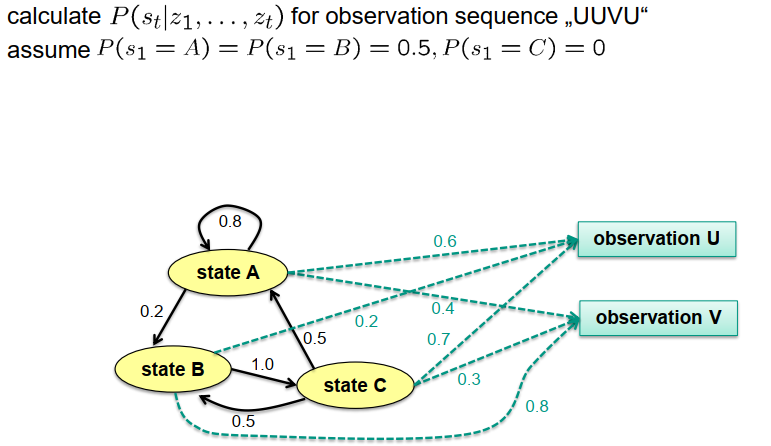
下面是这样一个表的示例。在左侧，我们有用椭圆表示的状态，黑色箭头表示状态之间的可能转换。箭头旁边的数字表示与每个转换相关的概率。请注意，还可能有表示系统保持在某个状态的概率的反射箭头。在这个示例中，我们对状态A有一个反射箭头，表示保持在状态A的概率为80%。

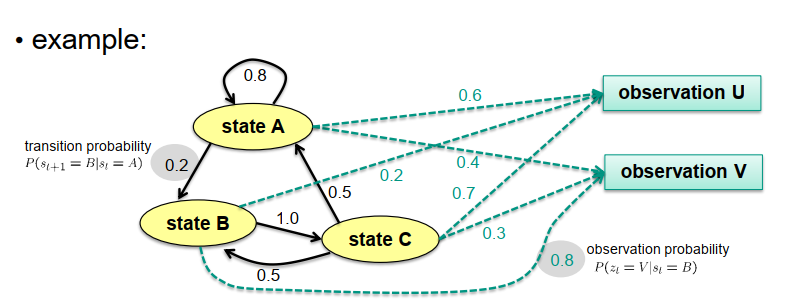
在右侧，我们有观测模型。在这种情况下，我们有两个观测，U和V。对于每个观测，我们有由虚线箭头和相应数字表示的观测概率。这些数字表示在我们假设处于某个状态时进行特定观测的概率。重要的是记住这些概率的顺序。此时，我们不关心观测特定测量时处于某个状态的可能性。相反，我们关注的是如果我们确定处于特定状态，进行某个观测的概率。这些概率对于建模传感器和其特性很有用。另一方面，我们在之前介绍的两步算法中旨在估计的概率是给定观测序列的情况下处于特定状态的概率。

还要记住，根据概率论，从一个状态出发的所有传出转换箭头的概率之和必须等于1。类似地，从同一状态开始的所有传出观测箭头的概率之和也必须等于1，以符合概率论的原则。

有了这个模型和表格，我们可以执行算法，并且例如确定在观测序列U、U、V、U之后处于状态A、B或C的概率。如果我们假设初始状态分布中A和B的概率都是0.5，初始状态为C的概率为0，我们可以计算所需的概率。

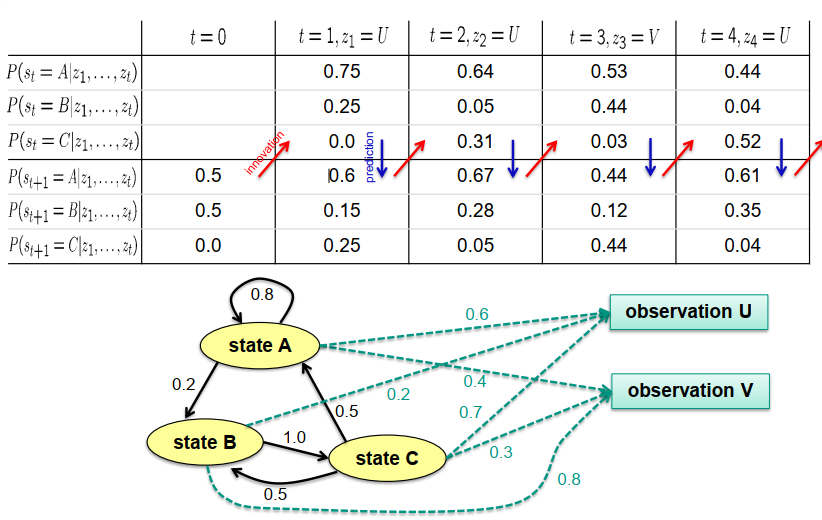
让我们为这个例子执行算法，从创新步骤开始。在初始化中，我们有预测的概率：预测概率为0.5时，我们处于状态A；预测概率为0.5时，我们处于状态B；概率为0.0时，我们处于状态C。

现在，当我们进行创新步骤时，我们将这个知识与观测概率相结合。在下面的图中，观测在状态A中观测到”u”的概率为0.6。我们将这两个项相乘：0.5乘以0.6等于0.3。然而，当我们回到之前的几张幻灯片中推导出的创新步骤的公式时，我们发现它不是一个等式，而是一个比例符号。这意味着我们还不知道概率是0.3，它可能是不同的，但我们知道概率与0.3成比例。

让我们计算状态B的概率。预测概率为0.5，观测概率从图中可以看出是0.2。我们得到0.5乘以0.2，得到0.1。

对于状态C，我们得到0.0作为上一个概率乘以观测概率的结果，在这种情况下观测概率为0.7，结果为零。

因此，我们知道对于状态A，概率与0.3成比例；对于状态B，概率与0.1成比例；对于状态C，概率与零成比例。根据概率论，这些概率必须相加等于1。

现在我们可以计算比例因子，即1除以(0.3 + 0.1 + 0)，即1除以0.4。

综合起来，对于状态A，我们得到0.3除以0.4，得到0.75。对于状态B，我们得到0.1除以0.4，得到0.25。对于状态C，我们得到0除以0.4，仍然是零。

现在我们已经计算了给定第一个观测的当前状态的概率。我们算法的下一步是应用预测步骤，由表格的上三行到下三行的蓝色箭头表示。让我们也执行这一步。

因此，我们要计算的是在下一步中我们处于状态A的概率。现在，我们必须考虑进入状态A或保持在状态A的所有方式。在第二个时间点上，处于状态A的可能性有三种。

第一种可能性是我们已经在状态A并保持在状态A。在第一个时间点上处于状态A的概率为0.75，保持在状态A的概率为0.8。因此，

我们得到此路径的概率为0.75乘以0.8。

第二种可能性是我们在时间点1处于状态B，但很不幸，从转换图中可以看出，至少没有直接的方式从状态B转移到状态A。因此，从B到A的转换概率为零，这种路径的概率也为零。

第三种可能性是我们在状态C，并进行状态转换到状态A。然而，在第一个时间点上处于状态C的概率为零，而转换概率为0.5。因此，两者的乘积为零。

剩下的是从A转到A的可能性，即0.75乘以0.8，得到0.6。

要计算在第二个时间点处于状态B的预测概率，我们需要考虑所有到达状态B的可能性。我们可能在时间点1处于状态A，概率为0.75，并以概率0.2转移到状态B。因此，我们得到0.75乘以0.2。

另一种可能性是我们在状态B并保持在状态B，但由于没有反射转换，无法沿此路径进行转换。因此，整体概率为零。

第三种可能性是我们在状态C并返回到状态B。然而，在第一个时间点上处于状态C的概率为零，因此此路径的整体概率也为零。

剩下的是0.75乘以0.2。

对于第三个状态，状态C的概率是多少？所有可能性：我们可以从状态A转移到状态C，但根据转换图，这是不可能的。第二种可能性是从状态B转移到状态C。这显然是可能的，并且最终概率为0.25乘以1。而在状态C并保持在那里的概率再次为零。

因此，我们得到的概率为0.25。

让我们执行创新步骤，然后进行预测步骤，再进行一次创新步骤和预测步骤。正如我们在前一张幻灯片中看到的表格，对于状态和观测由离散随机变量表示的情况，可以使用预测和创新步骤执行这个两步算法。我们可以将所有的概率存储在表格中。然而，当处理连续随机变量时，情况变得更加困难，因为表格已经不足以表示概率密度函数。

然而，至少从理论上讲，连续随机变量的情况并不真正更困难，因为我们已经看到可以使用相同的规则来处理概率密度函数，就像我们用来处理概率的规则一样。我们只需要用概率密度函数代替概率，用积分代替求和，然后得到表示创新步骤和预测步骤的公式。然而，在实践中，实现这些公式在计算机程序中却更加困难。

第一个问题是概率密度函数很难表示，我们无法列举所有可能的值并将它们存储在表格中。我们需要使用适当的概率密度函数类型。另一个问题是预测步骤中所需的积分可能难以在解析上表示。

Linear Gaussian Model 线性高斯模型

然而，好消息是，还有一种特殊情况可以解决并在解析上表示，这就是所谓的线性高斯模型。线性高斯模型意味着在隐藏马尔可夫模型中发生的所有操作都可以表示为线性操作，而所有随机项都被建模为高斯变量，即高斯概率密度。

这意味着在线性高斯模型中，状态转移公式是一个线性公式：St+1 = At * St + Ut + Epsilon t。在这里，At是一个适当的矩阵，Ut只是一个偏移量，Epsilon t是一个随机项。我们假设Epsilon t按照高斯分布分布。

在文献中，有时会以稍微不同的方式使用Ut作为控制输入，并与第二个矩阵B相乘，用于控制系统。但对于我们的目的，我们只处理测量部分，直接将Ut表示为一个常数偏移量就足够了。指数t表示这些矩阵At和偏移量Ut可能随着时间的推移而变化。它们不需要是常数；它们可以改变，但不能依赖于St。它们可以依赖于其他时间点上的内容，但不依赖于系统的当前状态。

所以，我们可以看到，我们对于转移模型的公式是关于St的线性函数，而所有的随机项都是高斯随机项。

类似地，对于观测方程，我们假设观测St可以通过将St与测量矩阵H相乘来得到。这个测量矩阵H可能也会随时间而变化，但它不能依赖于St+1。然而，它可能依赖于时间。另外，我们有一个额外的偏移量Delta t，它是一个随机项，用于模拟测量的不确定性。同样，我们假设Delta t按照高斯分布分布。

总结一下，该模型是线性的，并具有由矩阵At和偏移量Ut给出的线性状态转移。第二件事是Epsilon t是一个高斯随机变量，并且我们假设其均值为零。高斯分布通常被称为白噪声，因为没有偏移量。Epsilon t的协方差矩阵可能也随时间变化，但不能依赖于当前状态。

在该模型中，Ht表示用于推导观测结果的乘法因子，它可能取决于时间，但不取决于状态。Delta T表示测量噪声，假设为具有特定协方差矩阵RT的白噪声。协方差矩阵RT可以随时间变化，但不应取决于当前的状态或观测结果。

同时假设噪声项Epsilon T和Delta T是随机独立的。这个假设是构建隐藏马尔可夫模型所必需的。

需要注意的是，在文献中，可能会遇到省略了索引T的模型版本。这个版本假设矩阵A、U和H是常数，并且随时间不变。然而，这不是最一般的版本。在实践中，通常需要调整这些矩阵。例如，如果时间点不均匀或存在异步时间点，就需要修改矩阵A，以考虑上一个时间点和当前时间点之间的不同时间间隔。

总结起来，虽然该模型允许时间依赖性，但变量A、H、QT、RT和UT不应取决于当前的状态或观测结果。

Example

再举一个例子。回到观测匀速运动的车辆。我们已经知道可以用线性方式建模这种运动：x(t+1) = x(t) + （到上次观测的时间间隔）*（速度）+（额外的白噪声项），其中速度保持不变，还有一个额外的噪声项。

在这种情况下，delta T代表时间间隔，即两个步骤之间的时间间隔长度。epsilon项代表随机过渡噪声和速度测量中的随机不准确性。

因此，我们得到的状态表示如下：如果我们将这两个方程按矩阵-向量形式排列，可以写成：

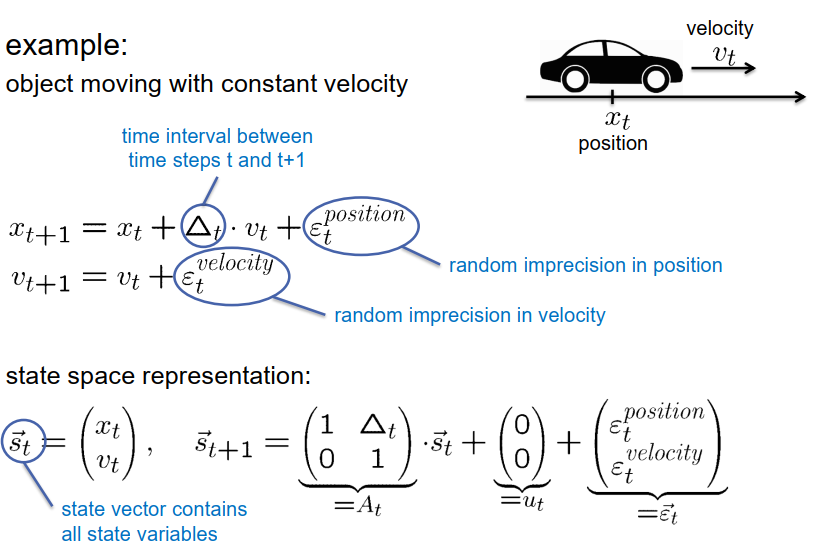
从这个形式中，我们可以得到我们需要的项：矩阵A(t)形式为[1 deltaT; 0 1]，偏移向量（在这种情况下为零向量），以及epsilon噪声项，其中包含位置和速度的两个噪声项。

现在，状态向量包含当前位置和速度。

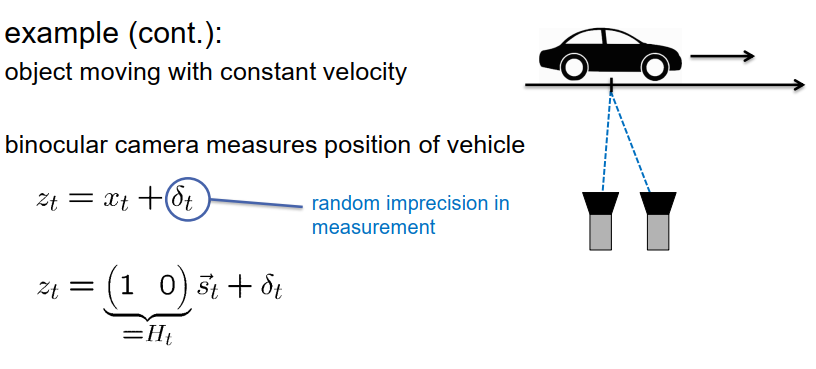
继续讨论观测问题，假设我们有一个立体摄像头设置，在每个时间点测量车辆的位置。因此，我们的测量集T等于x(t)加上一些测量噪声delta T。这可以重新写成我们需要的线性高斯模型的矩阵-向量乘法形式。

现在，矩阵H(t)是一个包含单行条目[1 0]的矩阵，适用于线性转换模型。如果当前状态概率分布是高斯分布，那么预测的下一个状态概率分布也是高斯分布。

这实现了预测步骤，将高斯分布映射到高斯分布。为了表示高斯分布，我们只需要知道mu向量（均值）和方差或协方差矩阵Sigma。因此，线性高斯模型的预测步骤接受一个mu向量和一个Sigma矩阵，并产生一个新的mu向量和一个新的Sigma矩阵。

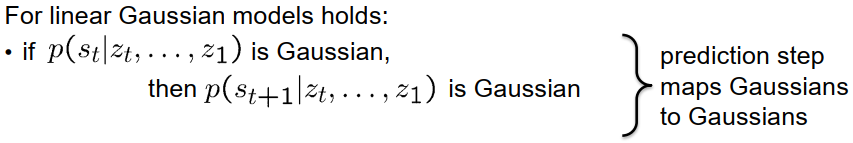
创新步骤类似。如果预测的状态概率分布是高斯分布，那么下一个状态的概率分布也是高斯分布。这意味着创新步骤将高斯分布映射到高斯分布。它接受一个mu向量、一个Sigma矩阵和一个测量，并产生一个新的mu向量和一个新的Sigma向量。这种高斯到高斯的映射非常有用，因为在这个算法中，我们只需要将mu和Sigma映射到新值，而无需表示具有数百个参数来描述形状的复杂概率密度函数。我们只需要这两个参数：mu和Sigma。

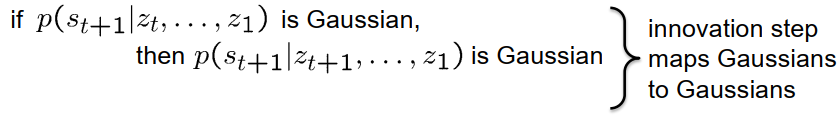
算法的结构如下：我们有两种类型的分布——状态分布和预测的状态分布，以及两个步骤——预测步骤和创新步骤。创新步骤集成了新的观测，而预测步骤预测了下一个时间点的状态分布。我们从一个初始的高斯状态分布开始整个过程，可以是预测的状态分布或状态分布，两种选择都可以。因此，第一步要么是创新步骤，要么是预测步骤。

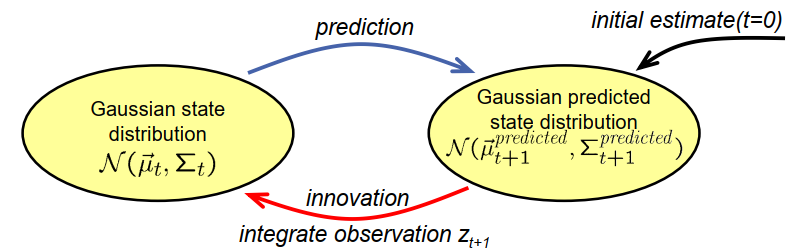
Kalman Filter 卡尔曼滤波

这个算法有一个名字，叫做卡尔曼滤波器。预测步骤在这里给出，正如所说的，预测步骤接受一个mu向量和一个Sigma矩阵，并返回一个新的mu向量和一个新的Sigma矩阵，现在用上标“predicted”来表示。我们可以推导出这个公式，但在这里的讲座中，我只给出结果，有趣的是，我们可以解释这个公式，例如，如果我们看一下MU值的公式，这里发生了什么，实际上我们只是将状态转移函数应用到先前的mu向量上，因此我们应用了状态转移矩阵A，并且在偏移量上不添加任何额外的噪声，因为我们想要估计状态而不是创建新的状态，但是要估计状态，我们在这一点上忽略了噪声。然而，当我们看到Sigma更新规则时，噪声就会出现了，在Sigma更新规则中，第一部分即将迄今为止的Sigma矩阵乘以A左乘和右乘只是将状态转移公式应用到Sigma协方差矩阵上，第二项额外的QT考虑了状态转移中的随机性，因此它反映了状态转移中的不准确性，并为我们的估计增加了一些不确定性，因此它告诉滤波器，预测的状态分布比先前的状态分布更加不确定，因为转换本身是嘈杂的，因此不确定性增加了。

创新步骤的形式如下：我们给定了从预测步骤获得的MU T predicted和Sigma T predicted值以及新的测量集T，然后我们得到mu T和sigma T。这里可以看到公式，我们首先计算一个中间变量KT，通常称为卡尔曼增益。正如你所看到的，它看起来有点复杂。然后我们计算新的mu T值，然后计算一个新的协方差矩阵Sigma T。

创新步骤的解释比预测步骤的解释更加困难，但我们可以将卡尔曼增益KT视为一种加权因子，它对迄今为止的知识和迄今为止的知识的不确定性进行加权。这种不确定性表示在Sigma predicted中，以及从测量中获得的不确定性，它们以逆矩阵的参数作为参数，例如h t乘以Sigma T predicted乘以h t的转置加上RT。这个部分有时会包含关于测量的不确定性的陈述，因此它计算了一种加权因子，然后这个加权因子在更新mu T U T时使用，在mu T U T的更新中，我们可以看到它是从预测的mu T开始计算的，加上一些加权因子KT乘以括号中的项。如果我们看一下括号中的项，我们会看到set T是当前的测量，h t乘以mu T predicted是我们预期的测量，如果mu T predicted是系统的真实状态，那么h t乘以mu T predicted就是我们预期的观测值。因此，这个括号的作用是将实际测量与预期测量进行比较，并基于此对MU值进行校正，即估计的状态。

对于表示Sigma更新规则的第三行的解释相对困难，因此对于这里发生的事情并没有一个简单的直观解释，但我们可以说，迄今为止的预测状态分布的不确定性与从测量中得到的不确定性以某种方式结合，而结果不确定性比先前的预测状态的不确定性更小，因为测量提供了一些额外的信息，使我们能够得到更好的估计。

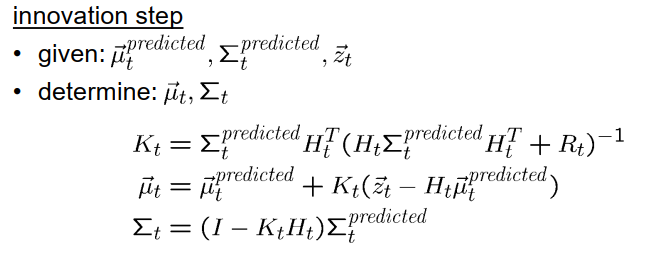
example:

让我们看一个简单的例子，再次是一个以恒定速度移动的汽车，我们假设我们每秒进行一次测量，这意味着我们的时间点在时间轴上等间隔地以一秒的距离分布。转换模型如下所示，这是我们已经推导出的，矩阵A与时间无关，是1 1 0 1，偏移向量是0 0，测量矩阵H是行向量1 0。

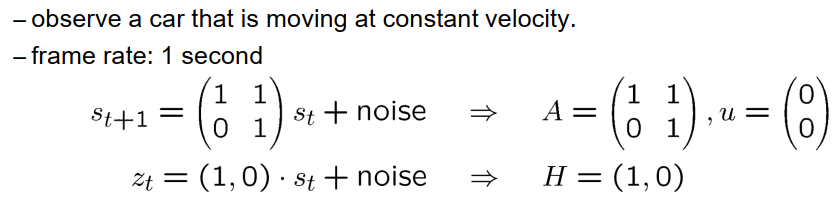
对于不确定性估计，即Q和R的估计，总是有点棘手的，一个粗略的想法是说，保持非对角线元素为零，并且对于对角线元素，考虑一下你预计的不确定性最大是什么，也就是你对应变量的错误最大预期是什么，然后取它的一半，并对其进行平方，这样就得到了一些合理的值，但你可能需要略微调整，得到这些矩阵的好值总是有点棘手的，对于我们这里的目的，让我们这样做，并使用这些矩阵。

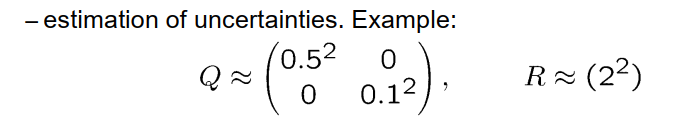
然后我们需要对状态进行初始分布，如果我们对起始状态一无所知，我们希望表达我们对它一无所知，我们该怎么办？思路是说，既然我们不知道是哪个状态，我们就随便取一个任意的mu值，例如0 0，出于数值原因，这是一个不错的选择。对于Sigma协方差矩阵，我们采用对角矩阵形式，将非对角线元素保持为零，对于对角线元素，我们取非常大的数值，例如1000的平方或者100的平方。这表示我们给出了一个初始猜测0 0，作为我们所能做的最好猜测，但我们也告诉你我们对它非常非常不确定。

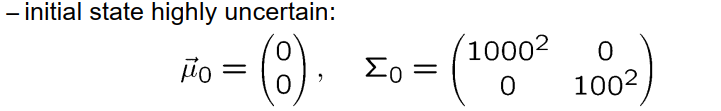
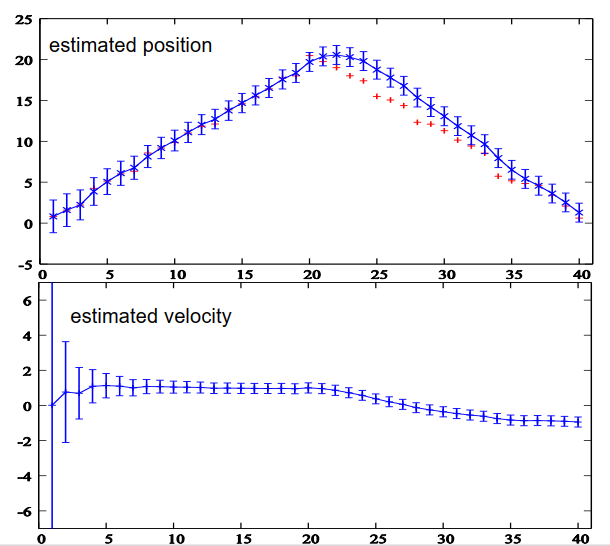
现在在Matlab中实现这个算法，并创建了一个小的测试环境并生成了一些测量数据，现在我们可以看到结果。在上面的图片中，水平轴表示时间，垂直轴表示位置，红色加号表示我们得到的位置测量值，蓝色叉表示估计的位置，即创新步骤的MU值，垂直条代表不确定性，这些条越大，协方差矩阵中对应的条目越大，也就是估计的不确定性越大。我们还可以看到估计的位置跟随真实位置，并且不确定性随时间稍微减小。我们还可以看到，与感知位置相比，估计位置更加平滑。

下方的图像显示了估计的速度，在第一个时间步中，我们得到了一个速度估计值为零，因为根据一个测量值无法估计速度，所以我们得到的初始估计值为零，但正如我们所看到的，我们非常不确定，因此卡尔曼滤波器告诉我们，是零，但我们不能确定它就是零，它也可能是其他值，例如在-7和+7之间。然后经过几次观察，滤波器基本上得到了正确的估计值，即在本例中为每秒一米的速度，我们可以清楚地看到不确定性减小，并且滤波器对车辆的速度越来越确定。不确定性不会变为零，在每个转换步骤中，都会再次添加一定的不确定性，但在本例中，它单调减小。

这是前一个例子的一个小变化，前22秒，车辆以每秒一米的速度向前行驶，然后在20秒后开始倒车，以每秒一米的速度向后行驶，正如我们所看到的，测量值在时间点20之前增加，然后再次线性减小。估计位置的滤波值在开始时非常接近真实位置，就像我们之前看到的例子一样，在时间点20处变得奇怪，因为滤波器仍然预期车辆以大致每秒一米的速度向前行驶，但实际上并非如此，整个建模的假设在某个时间点上被违反了，然后需要一段时间，卡尔曼滤波器才意识到车辆确实在倒车并适应新的运动方式，这是非常典型的情况，因为这里的实际情况在某个时间点与我们在隐马尔可夫模型中建模的情况有所不同，因此卡尔曼滤波器不能立即跟随新的行为。如果我们观察估计的速度，也可以看到相同的行为，开始时与之前的行为相同，在时间点20之后，我们可以看到需要多长时间估计的速度才会收敛到新的实际速度-1米/秒。有趣的是，不确定性并不增加，尽管估计的速度与实际速度不匹配，但这是由于卡尔曼滤波器的独立性假设，如果我们使用回归方法，并仅使用最后的5或10秒数据进行跟踪，那么情况将不同，我们会看到在这些情况下不确定性再次增加，当假设破裂时，但在卡尔曼滤波器中，不会发生这种情况。

所以，这是一个比较卡尔曼滤波器和线性回归方法的好时机，我们在本章开始时介绍了线性回归方法。

现在让我们使用非常相似的模型。两者都使用线性模型，并假设高斯噪声，因此它们非常相似。在卡尔曼滤波器中，我们希望估计一个状态向量，而线性回归中的回归系数扮演着状态向量的角色，所以它们也非常相似。然而，随机性假设略有不同。在卡尔曼滤波器中，我们有马尔可夫假设，假设状态转移与过去无关，并且观测与过去无关。但我们允许状态随时间变化。这在线性回归中是不同的。在线性回归中，我们假设观测在时间上是独立的，并经常用i.i.d.（独立同分布）来表示。然而，我们假设状态在时间上是恒定的，即状态向量不会改变。这是一个重要的区别。

在卡尔曼滤波器中进行的是增量计算，因此我们不需要存储过去的观测。我们只需要存储我们计算得到的最后一个mu和sigma值，这包含了我们进一步处理所需的所有知识。而在线性回归中，情况不同。在这里，我们需要重复计算回归，因此我们必须以某种方式存储我们要用于线性回归的所有观测。当然，我们可以在时间上使用滑动窗口，只使用最近的10或20个观测，并删除离开滑动窗口的观测。但对于滑动窗口内的观测，我们需要存储它们。

是这就是我们在这里看到的情况。因此，对于卡尔曼滤波器，我们只需要记住状态和协方差矩阵，而对于线性回归，我们需要记住所有的观测。

那么观测随时间的影响如何？在线性回归中，所有的观测对线性回归具有相同的影响。无论观测是旧的还是新的，它们对回归的影响基本相同。而在卡尔曼滤波器中，情况不同。如果你分析观测随时间的影响，你会发现随着时间的增加，观测的影响减小。这意味着旧观测只对当前状态估计有很小的影响，而新观测则有很强的影响。在线性回归中，我们也可以通过添加一些额外的权重来模拟这种情况，但在标准回归中，这种情况并不适用。

如果想要使用卡尔曼滤波器，状态和测量的噪声必须是已知的。因此，我们必须能够提供Q和R矩阵。这在使用卡尔曼滤波器时有时很难推导出来，是使用卡尔曼滤波器的一个重要障碍。而在线性回归中，我们不需要知道噪声，我们只需要知道噪声对所有测量都是相同的，但我们不需要提供任何关于噪声的协方差矩阵。这通常是一个优势。

我们从卡尔曼滤波器中得到的方差，也就是不确定性的测量结果，随时间基本上呈渐近下降的趋势。而在线性回归中，它们是变化的。有时它们变大，有时变小。

Nonlinear Extensions of the Kalman Filter 卡尔曼滤波的非线性扩展

在许多情况下，线性系统模型可能不可用，但需要使用非线性函数来以非线性方式描述系统。这个非线性函数被表示为f，它将时间t的当前状态映射到时间t+1的后继状态。此外，可能还存在一个非线性观测函数，表示为H，它将时间t的当前状态映射到时间t的当前观测集合。在这种情况下，标准的卡尔曼滤波器不适用。

在这种情况下，有几种可以用于扩展卡尔曼滤波器的方法，最简单的方法是使用所谓的扩展卡尔曼滤波器（EKF），它的一个变种是无损卡尔曼滤波器（UKF），还有一个非常通用的扩展是粒子滤波器。接下来，我们将介绍这三种滤波器的工作原理。

扩展卡尔曼滤波器使用数学技巧，将线性问题的解应用于非线性问题。其思想是在必要时通过使用一阶泰勒多项式作为非线性状态转移函数或观测函数的近似来线性化非线性问题。通过这样做，我们得到了以下形式的预测步骤：

扩展卡尔曼滤波器（EKF）使用数学技巧将线性问题的解应用于非线性问题。其思想是在必要时通过使用一阶泰勒多项式作为非线性状态转移函数或观测函数的近似来线性化非线性问题。通过这样做，我们得到了以下形式的预测步骤：

预测步骤： 预测状态向量：μ_t+1_predicted = f(μ_t) 更新协方差矩阵：Σ_t+1_predicted = F_t * Σ_t * F_t^T + Q_t

在这里，预期的状态向量μ_t具有状态向量的结构，因此我们可以直接应用状态转移函数f来获得预测的状态向量μ_t+1_predicted。然而，更新协方差矩阵并不直接。我们需要使用f的一阶泰勒多项式，而不是直接应用状态转移函数f。矩阵F_t表示非线性函数f在当前状态估计μ_t处的雅可比矩阵。

扩展卡尔曼滤波器的创新步骤与卡尔曼滤波器类似。卡尔曼增益的计算方式类似，但矩阵H_t不是像卡尔曼滤波器中的系统观测矩阵那样。相反，它表示观测函数h的一阶导数。在更新步骤中，我们直接将预测的状态向量μ_t+1_predicted应用于观测函数h，因为μ_t+1_predicted具有状态向量的结构。然而，我们仍然需要使用雅可比矩阵，因为协方差矩阵没有状态向量的形状。

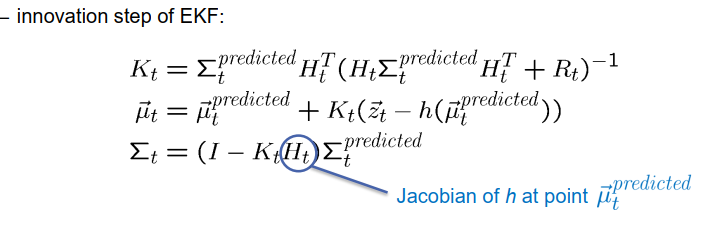
与扩展卡尔曼滤波器相比，无损卡尔曼滤波器(UKF) 使用了一种不同的线性化方法。其基本思想是使用代表性点称为Sigma点来表示高斯分布。在二维空间中，这些Sigma点可以被视为捕捉高斯分布形状的点。

在UKF中，高斯分布通过多个Sigma点而不仅仅是均值向量和协方差矩阵来表示。这些Sigma点被策略性地选择以捕捉高斯分布的形状和传播。通常情况下，对于二维高斯分布，会有五个Sigma点，包括一个位于中心（对应于均值向量）以及每个坐标轴上的两个点。这些点不一定与坐标轴对齐，而可以是倾斜的。

为了计算Sigma点，协方差矩阵被分成列向量，并且使用这些向量进行计算。具体的计算细节可以在文献中找到。

下一步是将状态转移函数应用于Sigma点，并将其映射到状态空间中适当的点，以表示后继状态的位置。由于Sigma点具有状态向量的结构，非线性函数f可以直接应用于它们。这样就可以在状态空间中获得其他五个点，表示状态的预测分布。

第三步是从这些Sigma点重新估计高斯分布。这涉及计算这些点的平均值和传播，以得出新的协方差矩阵和均值向量。再次强调，这些计算的具体细节可以在文献中找到。

到目前为止，我们已经将系统的非线性动态应用于代表性点。然而，为了考虑到这种转变中的不确定性，需要将协方差矩阵Q表示的附加高斯噪声添加到到目前为止获得的估计协方差矩阵中。

通过考虑这种附加的不确定性，我们可以实施预测步骤。创新步骤的工作方式类似，为当前状态分布创建Sigma点，然后将这些点应用于观测函数H。从中获得了观测的估计分布，并基于此进行校正步骤。

有关UKF及其实现的更详细信息，请参考相关文献。

Example: Determine Ego Motion Visually 通过视觉确定自我运动

首先，我们需要思考如何对问题进行建模，如何选择状态向量，如何使用转换模型，我们拥有哪些观察数据以及我们需要使用哪种观察模型。让我们从状态向量和状态转换函数开始。运动可以很容易地用速度来描述，因为我们有三个坐标轴，我们使用三个速度变量vx、vy和vz，来描述车辆在各个方向的运动。

此外，我们需要模拟车辆的转向。我们通过引入三个相对于三个坐标轴的角速度 Omega X、Omega Y 和 Omega Z 来实现这一点。所以总的来说，我们需要六个变量来描述车辆的运动，因此我们的状态向量包含这六个变量。

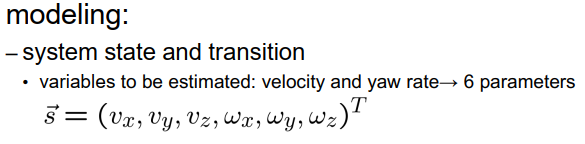
关于状态转换，我们假设至少在时间局部上，车辆是以恒定速度移动的。这意味着所有的速度变化都只是可能出现的一点点随机性，但总体上，车辆会保持其速度不变。这意味着状态转换模型相当简单，我们可以得出新状态在 t+1 时刻等于旧状态在 t 时刻，换句话说，St+1 等于单位矩阵乘以 St，当然还有一些额外的随机噪声，这些噪声模拟了驾驶员可能会稍微减速、稍微加速或稍微改变转向运动。

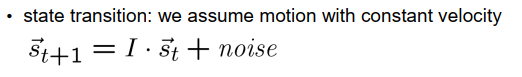
观察模型稍微复杂一些。让我们关注四张图片，从时间点 T 和时间点 T-1 的图片对，让我们讨论这些图片之间的关系。首先，我们分析这些图片并选择所有的特征点，例如 shift 特征点或者来自其他特征点方法的特征点。所以在这里，我用一个红色圆圈标出了其中一个特征点，我们可以看到，这个特征点在所有四张图片中的位置都不同，这是由于左摄像头与右摄像头的位置不同，以及摄像头设置在两个连续时间点的不同位置所致。现在，我们想在这四个看到该特征点的图像坐标之间建立一种关系。

首先，我们知道我们有一个立体相机对，这意味着如果我们在旧的图像对，也就是在时间点 T-1，我们可以取左右摄像头图像的两个位置，并根据这两个图像坐标计算出视差。基于这个计算，我们可以得到该点的三维位置，我们将其表示为 p p（蓝色符号 p p），下标大写的 P 代表前一张图片，第二个下标 L 或 R 代表左或右。

现在，如果我们知道或者至少对当前状态向量有一个好的猜测，那么我们就知道车辆的速度和角速度。这意味着，如果我们知道该特征点在空间中相对于车辆在时间点 T-1 的位置，如果我们知道车辆的速度，我们就不能预测这个点在时间点 t 时相对于车辆的位置会在哪里。这个三维位置用蓝色符号 p c 表示，大写的 C 代表当前时间点。

如果我们知道PC，也就是一个点的三维位置，我们可以很容易地使用针孔相机模型将它的位置投影到时间点T的相机图像中，从而得到位置PCL和PCR。我们可以看到，从PPL和PPR开始，通过PP到PC，最后计算PCL和PCR，有一系列的计算过程。这个计算过程是确定性的，当然是非线性的，因为计算一个点的深度需要非线性操作，而且当我们将点投影到图像中时，针孔相机模型也需要非线性操作。尽管我们可能难以将这一系列计算在一个公式中表达出来，但我们可以看到这是一种操作，或者是一系列相对不太复杂、可微分的计算过程。我们可以连贯地进行这些计算，从而建立一个观测模型。

这个观测模型以状态向量ST和前一图像中特征点的位置（我们视其为常数）为输入，计算出在当前时间点t的相机图像中，这些点的预期位置。正如我们在这里看到的，实际上这些操作中存在一些不确定性，因此我们需要添加一些小的高斯噪声。所以函数h是存在的，我们知道如何计算它，至少理论上我们可以把它写下来，虽然需要一些空间，而且我们知道它是非线性的，但是可微的。所以我们有一个非线性的观测模型，我们可以使用扩展卡尔曼滤波器或者无迹卡尔曼滤波器来估计车辆的自我运动，也就是状态向量。

总的来说，我们有一个六维的状态向量，包含了线性和角速度。我们有一个线性的状态转换模型，我们有一个非线性的观测模型，这意味着我们可以使用扩展卡尔曼滤波器或者无迹卡尔曼滤波器来估计状态向量。在这一点上，我要指出，实际上在图像中我们不只有一个特征点可以用于观测模型，我们有几十个，甚至几百个特征点可以用于观测模型。如果我们有几个这样的点，我们可以在观测模型中同时考虑所有这些特征点，这样做是为了减少运动估计中的误差。

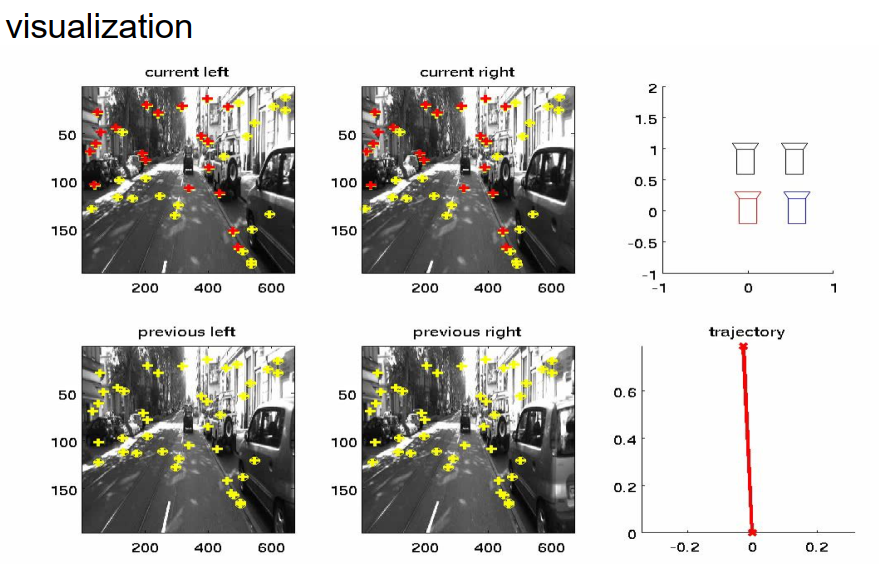
我们已经在软件中实现了这个想法，并在我们的实验车辆上进行了测试。在这张幻灯片上，你可以看到结果。四幅图显示了双目相机系统左右相机在现在时间点和之前时间点的相机图像。黄色的交叉线标记了用于鹰眼运动估计的特征点的位置。红色的交叉线是预测的特征点位置。红色和黄色的交叉线越接近，估计就越好。在右边，我们可以看到情况的顶视图。在右上角，我们可以看到现在时间点的四个相机的布局。相机的当前位置由黑色符号表示，而之前的位置由红色和蓝色符号表示。在右下角，我们可以看到车辆已经走过的路径的顶视图。这条轨迹是通过鹰眼运动估计并积分速度来估计的。

现在，让我们开始播放视频。

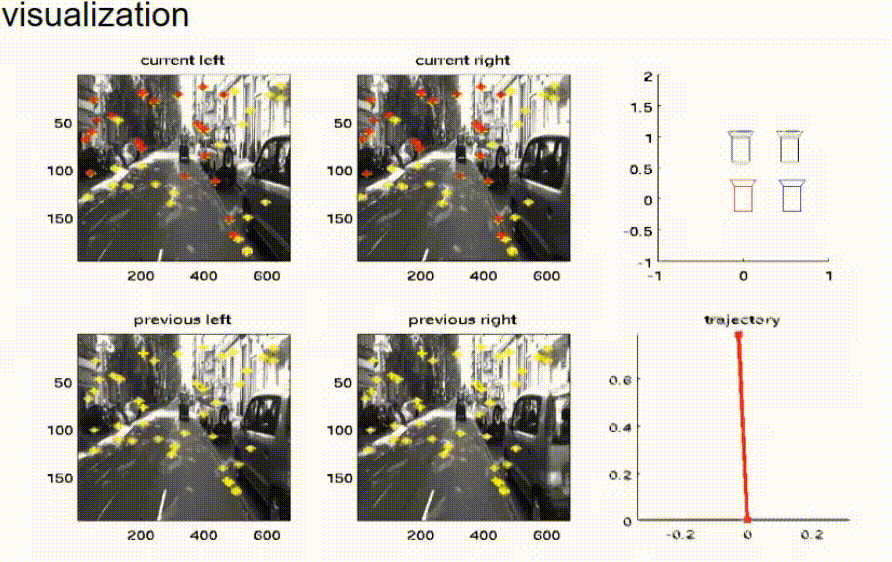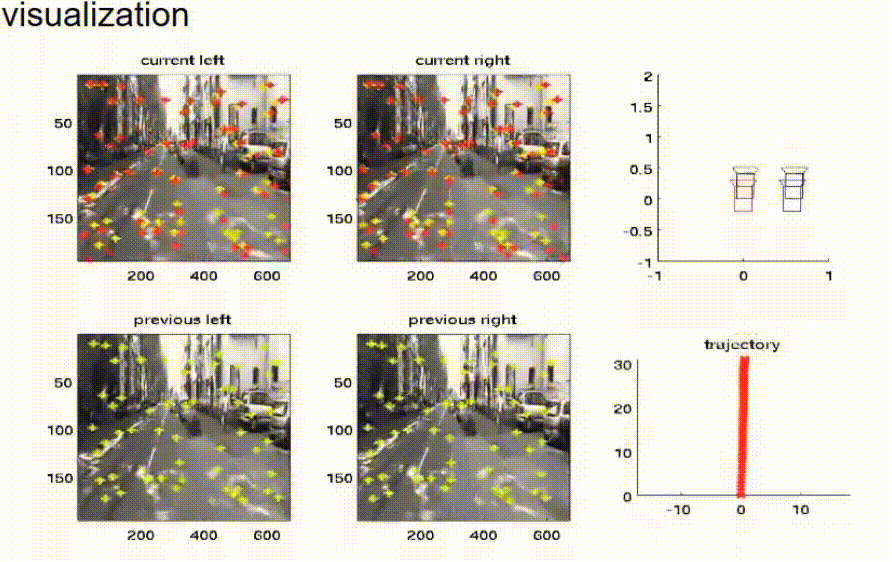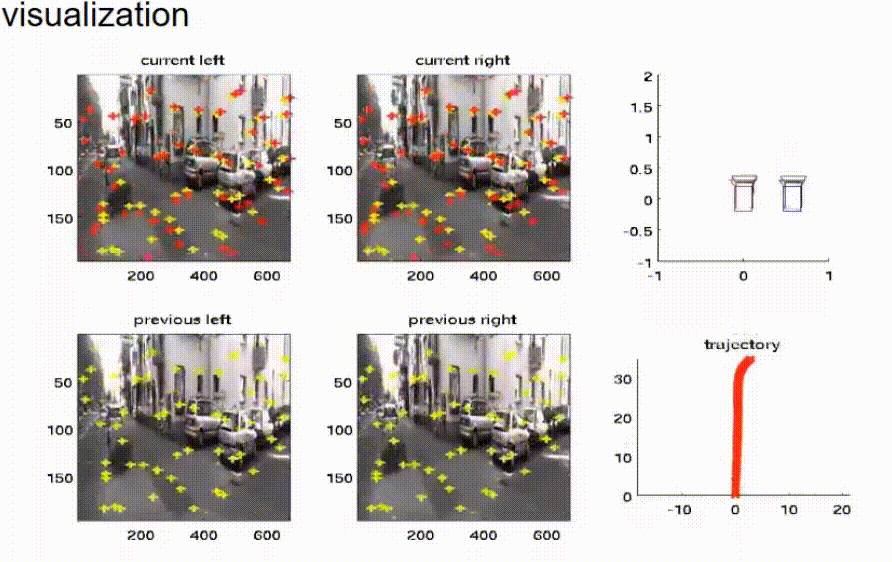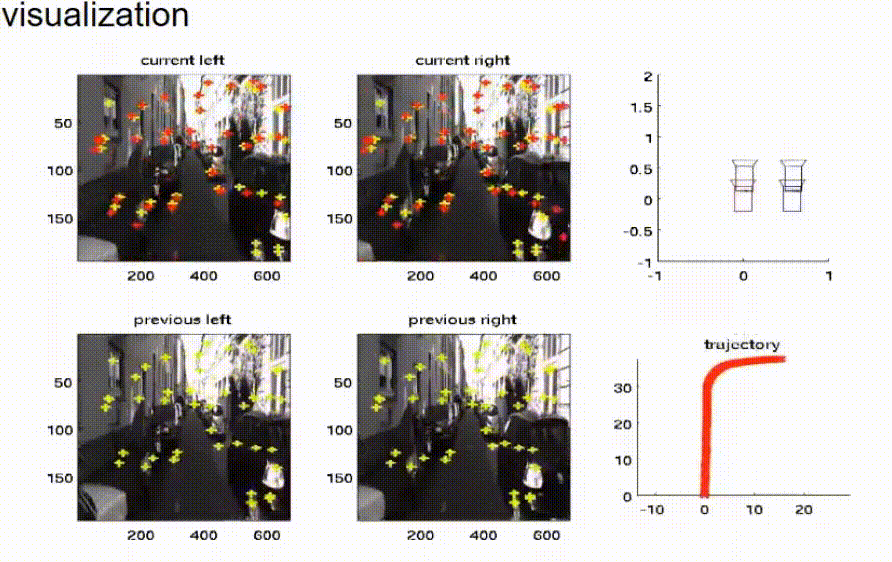
我们可以看到，估计的结果非常符合车辆的运动。现在，车辆停了下来，我们可以看到鹰眼运动也被估计为零。现在，车辆再次加速，我们可以清楚地看到，上一步和当前步骤的相机位置之间的距离正在增大。同样，估计的轨迹看起来相当好。在顶视图中，可以清楚地看到车辆驾驶的曲线。

以下视频显示了在复杂操作中鹰眼运动估计过程的行为。在顶部，你可以看到相机图像，底部是估计轨迹的顶视图。你可以看到两条线，一条蓝线和一条红线，一条是地面真实位置，另一条是车辆的估计位置或估计轨迹。尽管这个操作相当复杂，但估计的位置和估计的轨迹与地面真实情况相当接近。当然，由于估计过程中的随机性，两条曲线有轻微的偏差。

Non-Gaussian Models 非高斯模型

到目前为止，我们了解的卡尔曼滤波器及其非线性变体适用于所有噪声分布为高斯分布，系统动力学是线性的或至少在局部环境中接近线性的情况。然而，如果这些条件不再满足，也就是说，当我们处理非高斯分布或系统模型与线性函数偏差很大时，我们该怎么办？当然，我们仍然可以推导出当前状态的分布，给出了到目前为止所有的观测，以及未来状态的分布，给出了到目前为止所有的观测。这描述了预测步骤和创新步骤，它生成了预测状态分布和观察后状态分布之间的关系。在符号级别上，这仍然是可能写下来的。然而，这里出现的积分的计算和所有这些分布的表示变得困难。在这些情况下，我们需要对一般的概率密度进行数值表示。我们该如何做？哪些表示存在？我们可以用哪种表示来完成我们的任务？

Numerical Representation 数值表示法

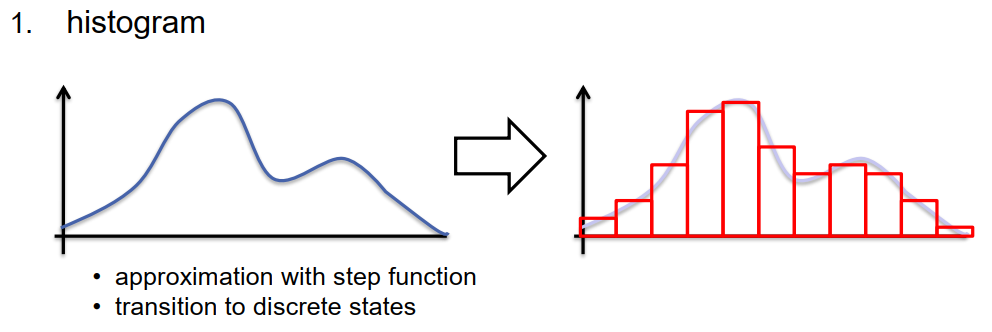
也许最常见的方法是用直方图来近似概率密度的数值表示。在直方图中，我们将随机变量的空间分割成不同的单元，并为每个单元计算随机变量取值在该单元内的概率。在连续随机变量的最简单情况下，我们用阶跃函数来近似概率密度函数，每个阶跃的高度表示随机变量在此阶跃所表示的区间内取值的概率。这是一种很好的方法，可以很容易地做到。结果是，我们通过对离散变量（即模拟连续随机变量的值落入哪个单元的变量）的分布来表示概率密度。对于离散随机变量，我们已经看到，我们可以使用我们的基本思想，即用创新步骤和预测步骤的算法来估计这个状态。然而，如果我们处理的是高维的状态空间，将这些空间划分为小的单元需要大量的单元，然后整个过程就会变得非常耗时和占用内存。所以，这可能不是表示概率密度的最好方法。一个关键的问题是，概率密度在大部分空间几乎为零，对于这些，我们需要为每个单元保存概率。然而，对于许多这样的单元，概率接近于零，所以我们在表示对我们来说完全不感兴趣的区域时浪费了时间和内存。

直方图的一个替代方案是使用随机样本来表示概率密度。我们做的是，我们会取一个概率密度和这种概率密度的随机数生成器，从这个分布生成一个随机样本。这在底部显示。所以，我们不是使用左边显示的密度函数，而是使用我们从这个分布中随机生成的一组点。这些点在幻灯片上作为小的红色刻度在x轴上显示。

现在，我们可以继续基于随机样本进行所有的计算，而不是直接在概率密度函数上进行计算。这个想法类似于无迹卡尔曼滤波器的做法，它也为分布生成一些代表性的点，然后仅在这些点上进行计算，而不是对整个密度函数进行计算。

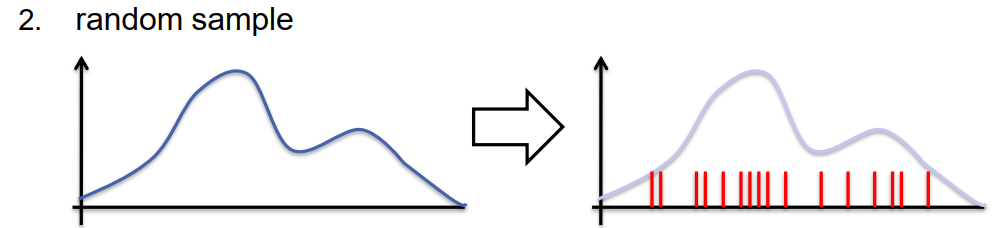
我们可以看到，对于这种表示，我们可以用更少的样本表示概率密度，因为我们只表示概率密度较高的区域，不表示那些密度几乎为零的区域。然而，这个问题的关键是，我们如何从这样的随机样本中生成新的样本？我们如何对新的样本进行预测，以及如何在观察到新的信息后更新这些样本？这个问题的答案就是粒子滤波器的基础，它是一种基于随机样本的贝叶斯滤波器，也被称为蒙特卡洛滤波器。在下一个章节，我会详细解释粒子滤波器的原理，以及如何用它来解决我们的自我运动估计问题。

那么我们应该如何选择权重呢？我们应该如何选择它们以使得加权样本可以在恰当的方式下代表概率分布呢？其中一个方法是使用一种称为重要性抽样的技术。在重要性抽样中，我们要处理的是一个目标分布，假设为p，它代表了我们想要建模的分布。我们有一个样本分布，假设为Q，它有另一个概率密度函数，如图中的绿色曲线所示。对于分布Q，我们需要有一个随机数生成器。对于p，我们不需要有这样的生成器。我们所做的就是从分布Q中抽取样本，使用该分布的随机数生成器。然而，我们当然想要表示的是分布p，而不是Q。为了处理p和Q之间的差异，我们使用了重要性权重。在所有目标分布p的概率密度函数明显大于我们已经从中生成随机样本的分布Q的概率密度函数的区域中，我们会增加权重。因为在这些区域，分布Q给了我们远少于我们预期得到的随机样本点。为了补偿这个区域的代表性不足，我们增加了重要性权重。

在其他区域，分布Q将会提供比我们需要表示分布p的随机样本点更多的样本点。在这些情况下，这个区域在样本中的代表性过高，因此我们降低了这些样本点的重要性权重。

在数学上，我们选择的重要性权重wi与pi(x_i)和Q(x_i)的比值成正比，其中x_i是我们从分布Q中生成的一个样本点。另外，我们必须保证所有重要性权重的总和等于1，这意味着我们可以把这些重要性权重解释为概率。把这些结合起来，最终产生了一个加权样本，尽管样本点x_i是从分布Q的随机生成器生成的，但最终表示的是分布p。这是一个很好的技巧，可以帮助我们在执行预测和创新算法时大有裨益。

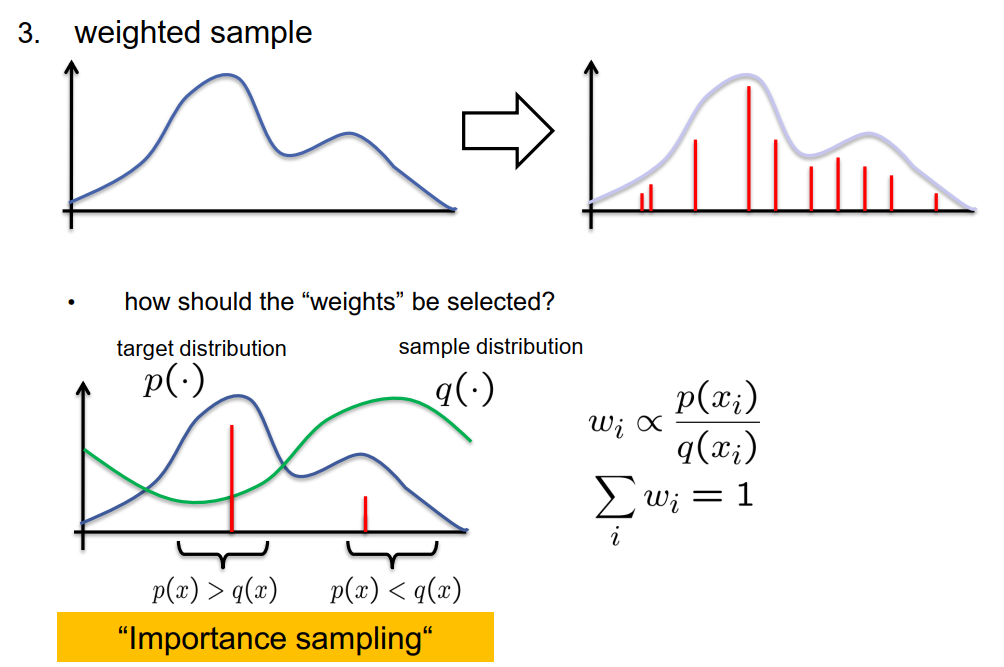
接下来我们来看看我们如何利用这些加权样本来实现创新和预测步骤。

Particle Filter 粒子滤波

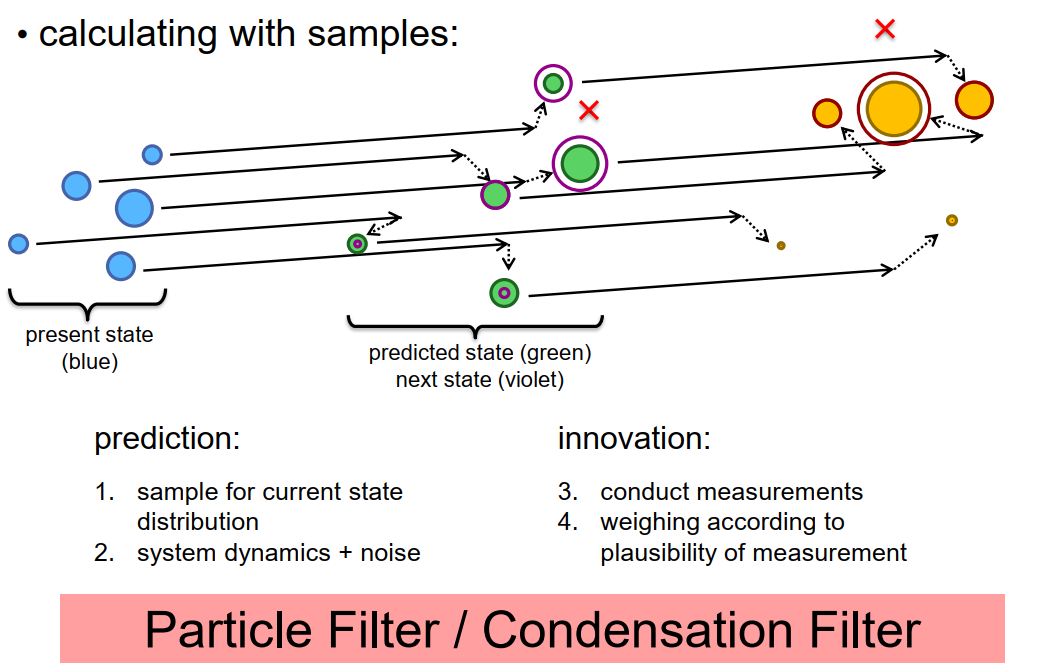
假设我们正在处理一个二维状态空间，这里的幻灯片实现了这个二维状态空间的平面。现在，幻灯片上的每一点代表一个状态向量。为了可视化，我们在这里显示了总共五个随机选择的状态向量。也就是说，这五个蓝点应该代表一个有五个元素的样本，这个样本代表了当前的状态分布。点的直径代表重要性权重w_i，直径越大，重要性权重就越大。所以，让我们假设这五个点是一个加权样本，代表了当前的状态分布。现在让我们想一个如何实现预测步骤的方法。

由于每个样本点都是一个状态向量，我们可以直接对其应用状态转移函数，即使它是一个非常非线性的函数。如果我们这么做，我们会把每个样本点都转换到状态空间的一个新位置。当然，我们必须考虑到状态转移模型不是一个确定性模型，还有一些不确定性，一些随机效应，导致新状态不仅仅是旧状态的转换，还有一定数量的随机性被添加进来或者以某种方式影响了结果。在这种情况下，我们可以生成一些非常小的随机位移，然后把它加到每个状态向量的结果位置上。也就是说，对于每个蓝色的样本点，我们首先应用转换函数，这用黑色的实心箭头表示。然后，我们生成一些小的随机数，把它加到状态转移的终点上，所以最后样本点的新位置是随机向量的终点。随机向量用虚线箭头表示。总的来说，我们以某种方式修改了随机样本，得到了用绿色点表示的样本。我们保持权重不变。

现在，我们假设我们得到了一个观察值。为了简单起见，让我们假设这里的观测值正好是状态加上一些随机误差。所以我们可以用红色的十字来表示测量值。现在我们能做什么呢？我们如何实现创新步骤呢？在创新步骤中，我们需要比较观测值和我们预期得到的观测值，然后得出结论。对于每个绿色的样本点（其实是状态空间中的向量），我们可以应用观测函数，这会给我们一个预期的观测值，如果绿色点是真正的状态向量的话。然后，我们可以直接比较这个预期的测量值和我们的真实测量值的匹配度如何。根据它们是否匹配，我们可以修改加权的随机样本。修改的最简单方法就是改变权重，也就是说，如果预期的测量值和感知的测量值非常匹配，就增加权重。如果感知的测量值和预期的测量值不匹配，就减少权重。这在图上用增加和减少点的直径来表示。现在，创新之后的随机样本集用紫色点表示。正如我们可以看到的，那些靠近测量值的点（也就是说，这些状态向量非常支持测量值），权重i增加。对于那些远离测量值的点（也就是说，状态向量并不支持测量值），权重会减少。

现在，我们可以继续下一个预测步骤了。我们从紫色的样本集开始，再次对每个点应用状态转移函数。然后，我们在位置上添加一些随机向量，以模拟状态转移中的随机性。我们得到的是用黄色表示的点集。

之后，我们又可以执行一个创新步骤，我们做一个观察，这在幻灯片上用红色十字表示。对于每一个样本向量，我们都会计算它们对这次测量的支持程度。对于那些很好地支持这次测量的样本，我们会增加其权重，而对于那些不支持这次测量的样本，我们会降低其权重。结果以红色圈表示。

就这样，我们可以继续进行下一个预测步骤，如此反复。这种技术被称为粒子滤波器，我们用来表示状态分布的点被称为粒子。也就是说，一个随机样本点连同其权重被称为一个粒子。是的，这个滤波器被称为粒子滤波器，有时也被称为冷凝滤波器。

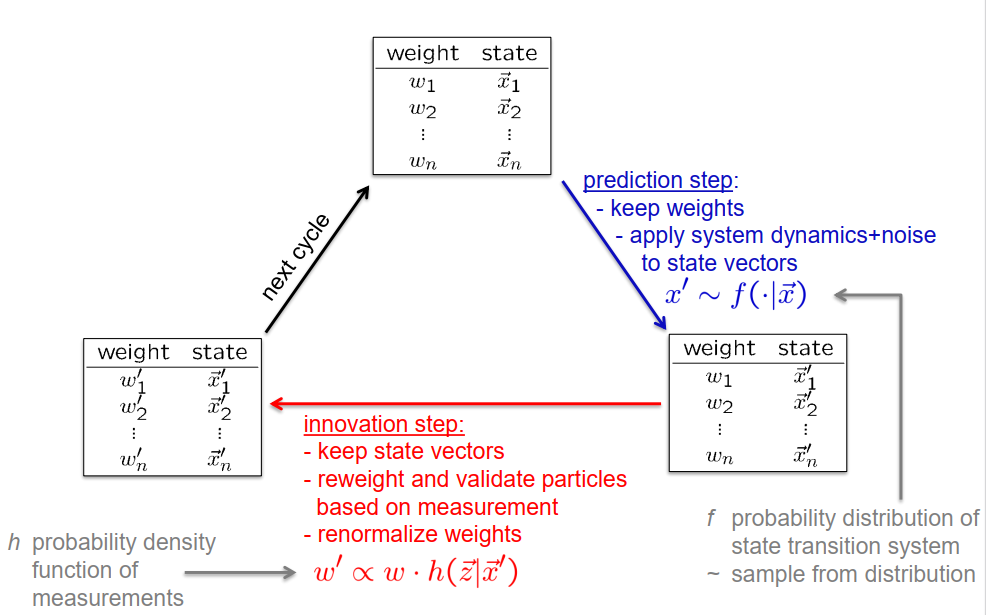
这张幻灯片展示了粒子滤波器的一般操作。它处理一组粒子，每一个粒子都由一个非负的重要性权重w_i和一个状态向量x_i组成，这个状态向量代表了关于当前状态分布的一部分知识。

在预测步骤中，我们按照以下方式操作这个粒子集：我们保持所有权重不变，但是我们改变状态向量。为此，我们从给定的前一状态x_i的后继状态的条件分布中生成新的状态向量。这用字母f表示。最简单的情况下，这可能是一个确定性状态转移函数和一个从描述系统转移中不确定性的概率分布生成的附加随机变异的组合。

下一步是创新步骤，我们假设我们进行了一组测量，基于这些测量，我们再次操作粒子集，但现在我们保持状态向量不变，只更新权重。我们选择新的权重与旧的权重和状态向量如何支持观察成比例。小h代表了一个依赖于状态向量的条件概率密度，它提供了我们期望得到的观测值的分布。这可以是像一个确定性观察函数加上一些概率密度函数，这个函数模型了在传感器过程中的不确定性。

在我们计算了这些权重之后，我们必须对它们进行归一化，使得所有权重的和等于1。

现在我们有了新的粒子集，我们可以进行下一个循环了。带有’的粒子集现在成为下一个循环的起点。

Example for Particle Filter

让我们看一个非常简单的例子。我们假设一个二维状态空间，我们在这个图中看到。我们进一步假设，状态随着时间的推移从点到点变化，但仅仅在水平坐标轴上产生一个偏移量，并且测量值简单地等于观察值加上一些随机噪声。

现在，让我们开始粒子滤波器，我们用一个盒区域的均匀分布初始化粒子集。在第一步预测步骤中，我们通过对其应用一个恒定偏移量并向右移动，并添加一些额外的随机向量来预测每一个样本点。结果以紫色圆圈表示。然后是创新步骤，我们做一个测量，这在图上用绿色星号表示。现在我们重新计算所有粒子的权重，结果是黄色或偏黄色的粒子集。如我们所见，那些接近观察值的粒子，它们非常支持这次观察，它们的权重增加，而那些不太支持测量的粒子，它们的权重在减小。现在是下一个预测步骤，我们根据状态动态移动所有粒子，并添加一些随机噪声。最终，我们得到的是以蓝色样本集表示的结果。再次应用创新步骤，我们得到一个测量，以绿色星号表示，并重新计算所有粒子的权重，这产生了青色粒子集。那些接近测量值的粒子，它们的权重在增加，那些远离测量值的粒子，它们的权重在减小。然后是下一个预测步骤，我们根据系统动态移动所有粒子，并添加一些随机噪声。之后，我们得到一个测量，并重新计算所有粒子的权重。

所以，这个程序工作得很好，但我们已经可以看到，有些粒子的权重在不断增长，也就是说，它们的权重变得越来越大，而其他粒子的权重变得越来越小，它们的权重在三次迭代之后已经非常接近于零，所以它们不再真正地对我们想要建模的分布有所贡献。如果我们继续这个过程更多步骤，我们会发现，最后只有少数粒子，可能是两三个，或者四个，甚至只有一个的权重明显不同于零，而其他所有粒子的权重都越来越接近于零，或者几乎等于零。这种粒子云的退化是个问题，因为只有那些权重明显不同于零的粒子真正地对分布有所贡献，而那些权重几乎为零的粒子不再贡献，它们只是增加了计算负担，但并不能帮助我们得到一个好的状态估计。

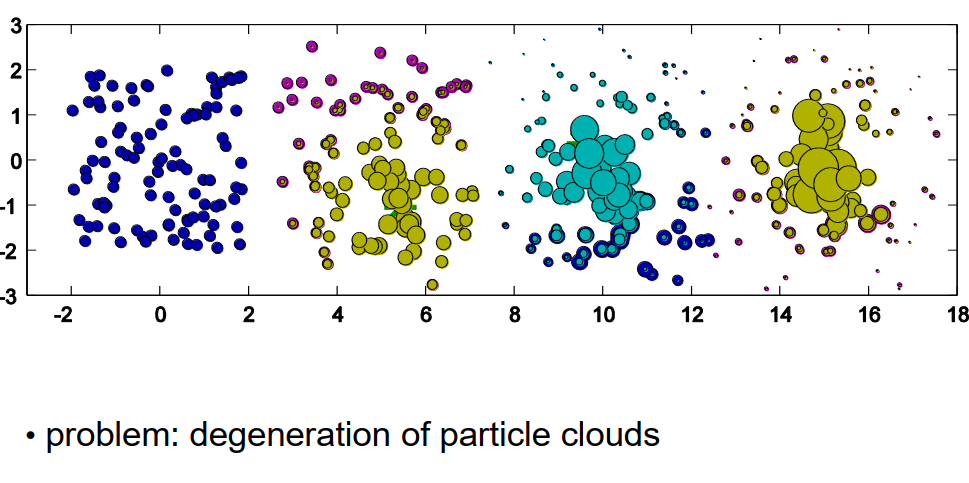
resampling 重采样

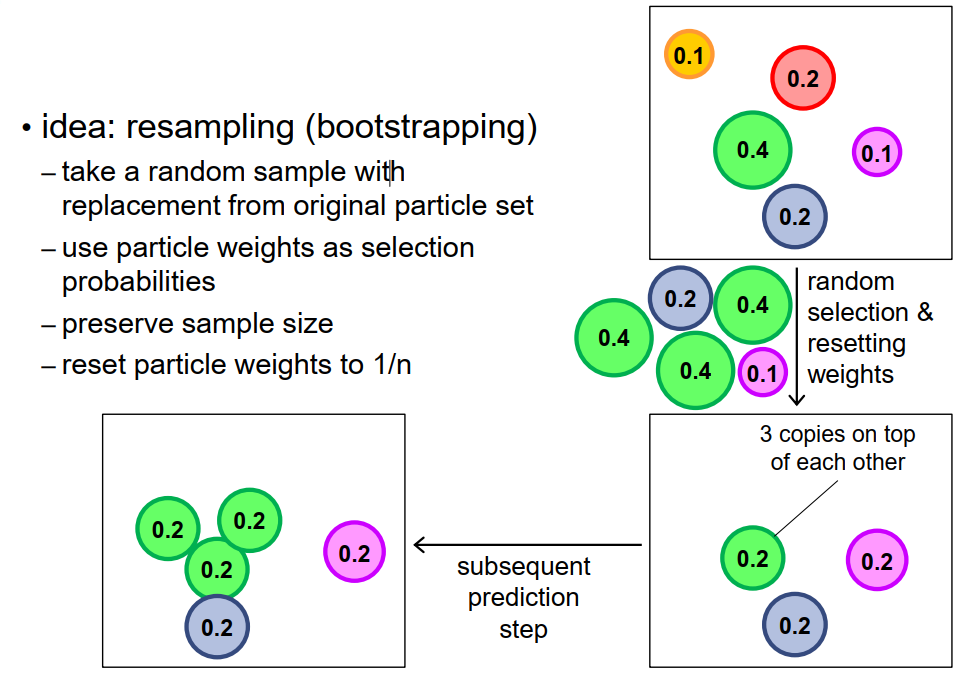
我们如何克服退化粒子集的问题呢？我们采用的技术来自于统计学，它被称为自举或重采样。所以我们拿到粒子集，我们创建一个新的集合，叫做自举样本，然后我们用自举样本替换原始的粒子集。那是怎么做到的呢？

为了说明，让我们假设我们有一个由五个粒子组成的粒子集，每一个粒子在这里都以不同的颜色表示，以便于我们后来再识别它们。

每个粒子的权重在圆圈内给出，我们可以看到这个粒子集是不平衡的，有些粒子有大的权重，比如绿色的，有些粒子有小的权重，比如黄色的或紫色的。

要创建自举样本，我们从该集合中随机选择粒子，并以选择某个粒子的概率等于该粒子的权重。所以在这种情况下，选择绿色粒子的概率是40%，选择红色的概率是20%，选择黄色的概率是10%，等等。我们可以在我们的自举样本中多次取同一个粒子，也就是说，这是一种有替代的采样。所以在这个例子中，让我们假设我们取了三次绿色的粒子，一次蓝色的粒子，一次紫色的粒子。你会看到，总的来说，粒子的数量保持不变。然而，有些粒子出现了几次，而其他粒子一次都没有出现在自举样本中，特别是那些有高权重的粒子出现了几次，而那些权重小的粒子，他们经常在自举样本中再也不出现。最后，我们将自举样本中所有粒子的权重重置为1/n，其中n是粒子的数量，这样我们最后得到的粒子都有相同的权重。底部的图片显示了结果，注意绿色的粒子出现了三次，所以我们在这里有三个相同的粒子的副本。当然，这有点难以显示，为此，你只看到一个，但你可以看到标注，确实，绿色的粒子在这里有三个副本。现在我们继续粒子滤波器，就像之前一样，我们可以开始预测步骤，然后创新步骤，然后我们会得到新的权重。现在，你可以看到，这个新的粒子集比原来的粒子集更平衡了。

重采样是一个很有效的工具，可以避免粒子集的退化，但它也有一些缺点。重采样的一个主要缺点是，由于有放回的抽样，有些粒子在重采样过程中可能会被多次选中，而有些粒子可能一次也不会被选中，这可能导致一些重要的信息丢失。此外，如果我们太频繁地进行重采样，那么这个方法就可能导致过度拟合，这就是所谓的重采样退化。为了解决这个问题，通常的做法是使用某种准则来决定何时进行重采样，例如，当有效粒子数下降到总数的一定比例时。有效粒子数可以通过计算所有粒子权重的平方和的倒数来得到。

这就是粒子滤波器的基本原理。在实际应用中，可能会使用更复杂的版本，其中包括不同类型的预测和更新步骤，以及更复杂的重采样策略。

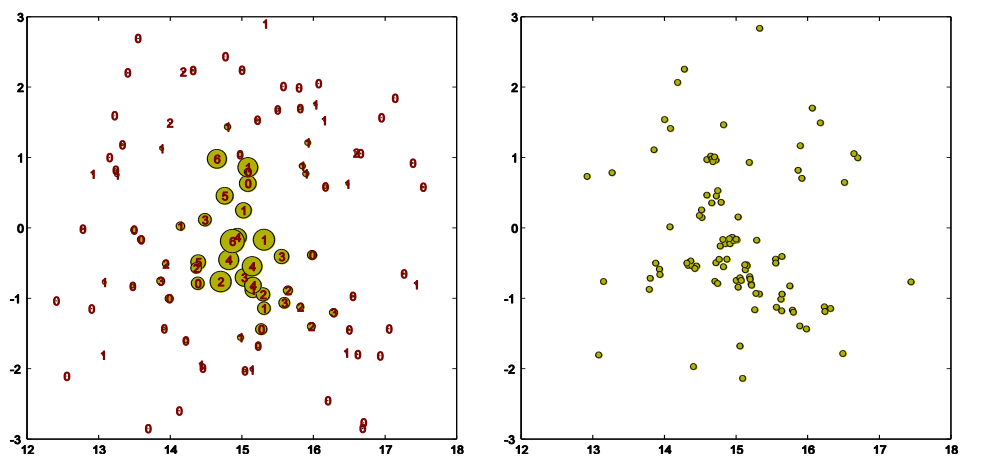
当我们考虑用粒子来建模分布时，我们会遇到这样的退化粒子集，圆圈的直径表示权重，我们看到在边缘有非常非常小权重的微小粒子，而在中心有相当大权重的粒子。现在我们开始重新采样的过程，我们随机从集合中选择粒子，结果可能是这样的。红色的数字表示我们选择某个粒子的次数，例如，在中心我们发现粒子被选择了6次或4次或5次，而在边缘那些粒子只被选择了一次或甚至一次都没有。所以现在我们取那些选中的粒子，我们把他们的权重重置为1/n，然后情况就变成了这样。请注意，图片中间有几个粒子在同一个地方重复出现，所以我们只看到一个，尽管有几个粒子在同一个地方。为了更好地可视化，让我们给这些粒子加上一点随机噪声，这样我们就可以看到在中心确实比在边缘留下了更多的粒子。

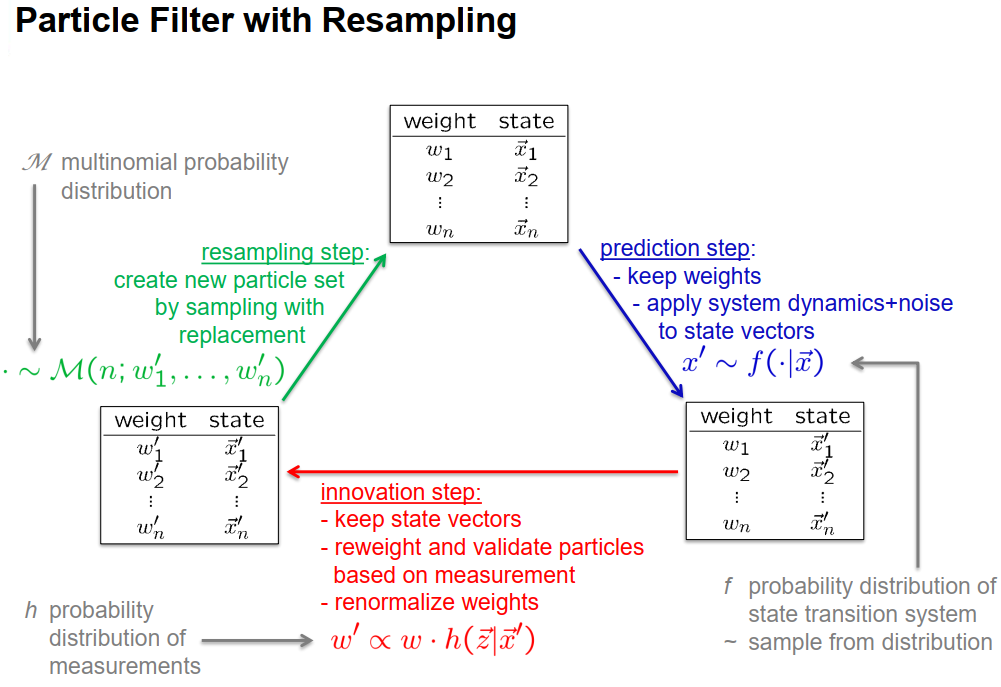
所以让我们再看一下带有重采样的粒子滤波器的操作。我们从一个具有权重wi和状态向量xi的粒子集开始，第一步是预测步骤，我们已经知道这一步。下一步是创新步骤，这也是和我们之前做的一样。现在，我们不再把在创新步骤中获得的这个粒子集作为下一个预测步骤的起点，我们在两者之间做一个重采样步骤。这意味着我们通过替换采样创建一个新的粒子集，这个幕后的M字母在这个幻灯片上表示一个多项概率分布，这意味着一个概率分布，描述了我们有n个可能的粒子可以选择，选择每个粒子的概率与重要性权重成正比，我们选择n个新粒子，这意味着粒子集的大小保持不变。

重采样的粒子集现在成为下一个预测步骤的起点，就像这样我们继续。所以，粒子滤波器的重采样包括三个步骤：

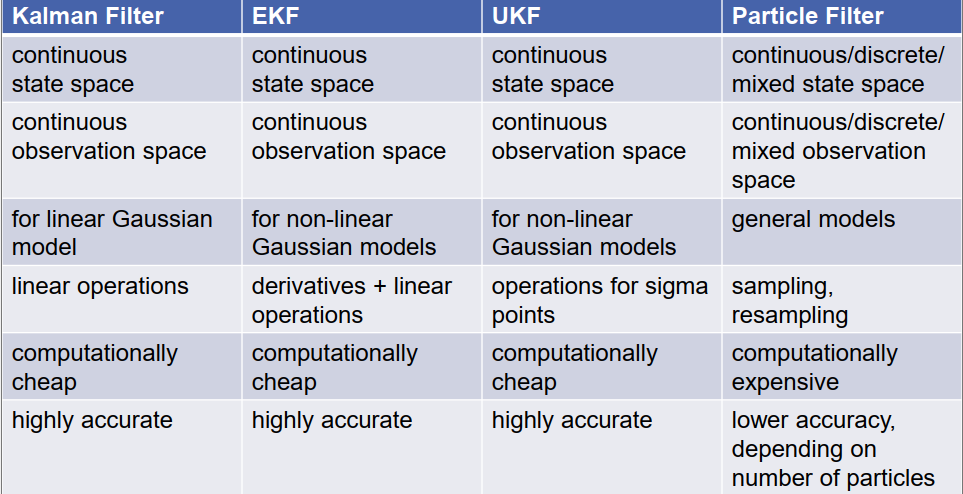
让我们比较一下我们在这一章中得到的过滤器，卡尔曼滤波器，扩展卡尔曼滤波器，无迹卡尔曼滤波器和粒子滤波器。卡尔曼滤波器，扩展卡尔曼滤波器和无迹卡尔曼滤波器都是在连续状态变量上工作的，这创造了数据变量不能被这些滤波器包含在内。粒子滤波器更通用，它可以处理连续随机变量，离散随机变量，也可以处理这些类型随机变量的混合。也就是说，状态向量可能由一些连续随机变量和一些离散随机变量组成。在观测空间中，我们有同样的情况，所以卡尔曼滤波器，扩展卡尔曼滤波器和无迹卡尔曼滤波器只能处理连续的观测变量，所以测量值是实数。粒子滤波器再次很通用，所以它可以处理连续和离散的观测，它也可以处理两者的组合。我们可以在卡尔曼滤波器中使用什么模型？当然，我们只能使用线性高斯模型。对于扩展卡尔曼滤波器和无迹卡尔曼滤波器，我们可以放宽这些条件，我们坚持高斯模型，但是转换函数和观测函数可能是非线性的，至少稍微非线性。粒子滤波器并不限制分布的种类和转换函数的种类，它可以处理任何模型。

我们需要执行哪些操作来执行卡尔曼滤波器或其他滤波器？在卡尔曼滤波器中，我们只需要线性操作，乘法矩阵，加上向量和矩阵，最复杂的操作是计算一个矩阵的逆。对于扩展卡尔曼滤波器，情况也一样，此外，我们还要计算导数，也就是状态转换函数和测量函数的雅可比。在无迹卡尔曼滤波器中，我们需要生成Sigma点，然后对Sigma点进行操作。在粒子滤波器中，我们需要的是采样和重采样，所以只是一些随机化操作。

这些我们需要的操作在计算上都相当cheap，至少对于卡尔曼滤波器来说，只要状态空间不是太大。当然，反转一个500x500的矩阵并不容易，但是对于相当小的状态空间，卡尔曼滤波器的操作并不计算昂贵。对于扩展卡尔曼滤波器，情况几乎相同，只是导数的计算可能需要一些额外的工作量。对于无迹卡尔曼滤波器，计算的计算工作量仍然很小，我们需要在Sigma点上应用状态转换函数，Sigma点的数量与状态轴的数量线性减小，这意味着状态变量的数量。对于粒子滤波器，我们得到了每个粒子非常简单和便宜的操作，然而，因为我们通常有数百个，数千个甚至数百万个粒子，所以粒子滤波器在计算上要昂贵得多。所以，更大的计算开销让我们可以处理更复杂的模型。我们得到的结果的准确性如何？当然，这只适用于满足各自滤波器条件的情况。如果我们可以应用一个卡尔曼滤波器，并且模型真的是一个高斯线性模型，那么卡尔曼滤波器的结果将是高度准确的。对于扩展卡尔曼滤波器和无迹卡尔曼滤波器，只要转换和测量函数不是太离线性，情况也是一样的。对于粒子滤波器，准确性高度依赖于粒子数量。对于小的粒子集，准确性较低。对于非常大的粒子集，可能有数百万或数十亿的粒子，准确性与卡尔曼滤波器一样高。然而，在实践中，你通常不能承担为数百万或数十亿粒子做所有的计算，因此，在实践中的准确性通常较低。我们将在第六章看到一个粒子滤波器的例子，它用于自我定位。

总结：这一章讲述了在三维空间中跟踪对象。我们从回归作为跟踪对象的技术开始，主要关注线性运动模型，这是一种不需要太多先验信息就能成功的简单技术，所以如果可能的话，尝试使用回归模型。然后我们转向马尔可夫过渡模型，即隐藏马尔可夫，我们描述了系统状态，我们提到了马尔可夫假设的随机独立性，这是非常重要的，因为它使得在这种模型中进行有效计算成为可能。最后，我们推导出了一个通用的滤波器模板，其中包含了预测和创新步骤，用来从一系列观测中估计这样一个隐藏马尔可夫模型的状态。

基于隐藏马尔可夫模型的滤波器主要分为两类：卡尔曼滤波器家族和粒子滤波器。卡尔曼滤波器，包括扩展卡尔曼滤波器和无迹卡尔曼滤波器，适用于线性高斯模型或至少接近线性高斯模型的情况。如果我们不能满足这些限制条件，那么我们就要转向粒子滤波器，它更加通用，可以处理任何形式的模型。然而，代价是在计算方面要更加消耗资源。