Chapter 4: Optical Flow and Image Based Tracking
光流和基于图像的跟踪
欢迎来到《汽车视觉》讲座中关于光流和基于图像的跟踪的章节。
首先,让我们看一下文献。这里有几篇来自教科书和原创论文的章节,涉及到今天讨论的主题。前三个条目是教科书的一部分,介绍了光流估计的主题。第四篇出版物是一篇原创论文,描述了Hon和Chun的方法。如果你有兴趣阅读原始论文,最后一篇论文涉及内核化相关滤波器,这在本章后半部分讨论图像中的物体跟踪时已经介绍过。
References
- B. Jähne, Digitale Bildverarbeitung, Springer, 2005, Chapter 14
- E.R. Davies, Machine Vision. Theory. Algorithms. Practicalities. Elsevier, 2005,Section 21.6 ff
- R. Jain, R. Kasturi, B. G. Schunck, Machine Vision. McGraw Hill, 1995, Section 14.1-14.4
- B. K. P. Horn, B. G. Schunck, Determining Optical Flow. Artificial Intelligence 17, 1981, pg. 185-203
- J. F. Henriques, R. Caseiro, P. Martins, J. Batista, High-Speed Tracking with Kernelized Correlation Filters, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 37, no. 3, pp. 583-596, 2015
Image Sequences 图像序列
到目前为止,我们已经研究了单幅灰度图像或双目摄像头设置中的成对灰度图像。现在,我们想把这种分析扩展到随着时间推移记录的灰度图像序列。为此,我们用第三个变量T来扩展灰度函数,它代表记录的时间。在我们的案例中,我们将T解释为一个整数,用来计算到现在为止记录的图像数量。
到目前为止我们有:
- examined single images $g(u, v)$
- examined stereo images $\left(g_l(u, v), g_r(u, v)\right)$
图像序列:
- examine a sequence of images $g(u, v, t)$
- 观测图像随时间的变化
- 自我运动(ego motion)引起的变化
- 观察物体运动引起的变化
Optical Flow 光流
光流是由相机和观察对象之间的相对运动引起的图像中任何点的明显移动
我们感兴趣的是观察图像序列中发生的变化,这些变化可能是由相机的自我运动、图像中观察到的物体的运动或两者的组合引起的。
这就引出了光流的第一个定义: 光流是图像中任何一点的明显移动,由相机和被观察物体之间的相对运动引起。重要的是要看到,光流是图像空间中的一个属性。它是图像坐标中的一个矢量,它连接了前一幅图像中某一点的位置和后一幅图像中同一点的位置。它不是一个物体的三维运动,而是图像空间中的二维运动。
这里我们有一个非常简单的例子,就是两幅图像一个接一个地记录下来,我们可以很容易地观察到一些光流。我们可以看到情况是如何变化的,某些点是如何在两幅图像之间移动的,这种移动就是光流。我们可以区分两种不同的光流概念。

第一个概念叫做密集流,我们的目标是为图像中的每一个点计算一个流向量,或者至少计算尽可能多的点,从而形成一个完整的流场或流向量场。
第二个概念是稀疏流,我们只对获得特定兴趣点的光流向量感兴趣,例如图像中突出特征点的一个子集。这建议使用特征点方法,我们分析每张图像,检测特征点,然后比较第一张图像中的哪些特征点也能在随后的图像中找到。这种方法使我们能够为特征点创建稀疏的流向量。
然而,这并不足以实现密集流,因为图像中的许多点不是特征点,我们用这种方法不会得到这些点的流向量。
– 密集流:我们确定图像中每个点的流矢量 – 稀疏流:我们仅为(一小部分)显着点(例如特征点)确定流向量
Typical Optical Flow Fields 典型光流场
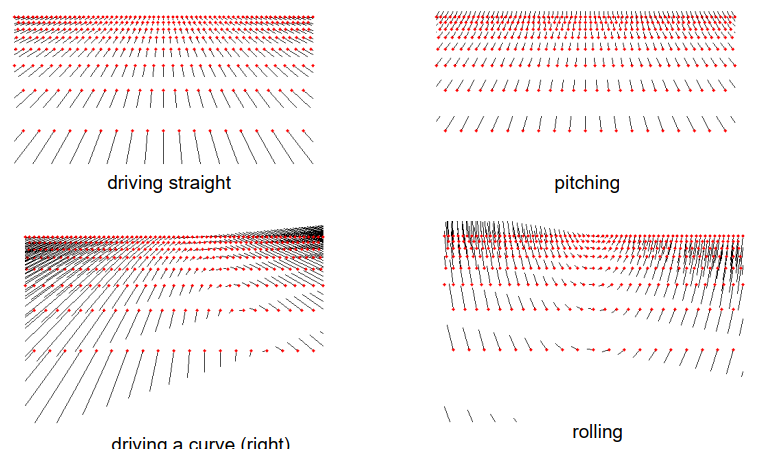
现在,让我们研究一下在某些情况下我们可以期待的典型流场。让我们假设我们有一个平面世界,在这个世界里,一辆车正笔直地向前行驶,我们观察到地面在一条水平线以下。在这些条件下得到的光流向量显示在左上方的图像中。每个流向量都用黑线标出,红色菱形表示第一幅图像中的相应点。
我们可以观察到,流动向量正在向地平线上的一个虚拟点靠拢,流动向量的长度根据与摄像机的距离而变化。点越远,流动矢量越小。在天空中,我们无法确定任何流动矢量,因为那些点实际上位于很远的地方,导致流动等于零。
第二张图片描述了一个类似的情况,但有一个俯仰运动。如果我们想象坐在一辆汽车里,有人把车头往下推,然后松开,造成俯仰运动,流场看起来与直行驾驶的情况类似。然而,在这种情况下,我们在地平线上仍然有不同于零的流向,而且流向的整体方向也不同。
第三张图片显示了滚动运动,当车辆沿其纵轴倾斜时,就会出现这种情况,就像摩托车在弯道上行驶一样。流场表现为滚动运动。当然,这种滚动运动也可以与直线行驶的运动相结合,导致不同的整体流场,如第四张图片所描述的,车辆向右行驶通过一个曲线。
道路上的预期流
假设:
- 光照是恒定的。
- 目标点没有被遮挡。
这些是我们在这些情况下可能观察到的典型光流场。只是为了让您对其外观有一个概念。现在让我们讨论如何计算光流。一种方法是了解场景中所有物体的真实运动和三维场景结构,然后可以计算光流。然而,这不是我们的目的。我们的目标是直接从图像序列中提取光流。
为了做到这一点,我们做出了一些假设。首先,我们假设图像序列是在恒定照明下记录的,这意味着每个点的亮度随时间不变。第二个假设是我们要观察的点不会在视频序列中的任何图像中被遮挡。如果被遮挡,我们就无法计算光流。这个假设是相当明显的。
基于这些假设,我们为光流建立了一个条件。我们引入光流向量ΔUΔV,描述了某个点的光流,表示为U B。
由于我们假设该点的照明在时间上不变,我们可以得出结论,先前图像中该点的灰度值(在时间T)必须等于稍后图像中位置为U + ΔU,V + ΔV,T + ΔT的像素的灰度值。这个必要条件要求ΔUΔV是位置U,V处点的光流。然而,这还不足够,因为可能有许多点满足这个等式。
从这个必要条件出发,我们想推导出如何计算ΔU和ΔV。我们从等式的两边减去U,V,T处的灰度G,然后用一阶泰勒多项式替换右边的第一部分。这得到了一个名为“运动约束方程”的方程。这个方程提供了一个条件,必须满足ΔUΔV才能成为某个像素位置的光流。
重要的是要注意,运动约束方程中需要的所有偏导数都是在用于计算光流的第一个图像对的某个位置处计算的。
光流的必要条件:
\[g(u, v, t)=g(u+\Delta u, v+\Delta v, t+\Delta t)\]- 必要但不充分。
- 不够清晰
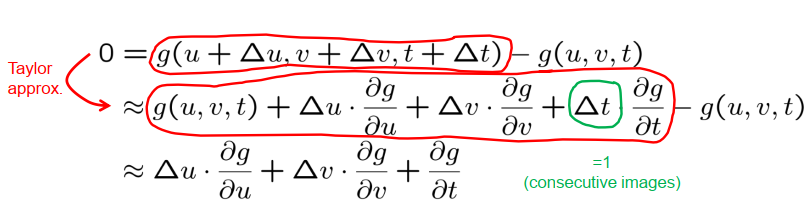
运动约束方程:
\[-\frac{\partial g}{\partial t}=\Delta u \cdot \frac{\partial g}{\partial u}+\Delta v \cdot \frac{\partial g}{\partial v}\]– 偏导数从何而来?
使用导数滤波器掩模(例如Sobel)进行滤波会产生$\frac{\partial g}{\partial u}, \frac{\partial g}{\partial v}$
灰度值差异产生 $\frac{\partial g}{\partial t} \approx g(u, v, t+1)-g(u, v, t)$
那么,我们如何计算这些偏导数呢?关于U和V的偏导数是我们在本课程的第一章中已经推导出来的。我们可以使用滤波器掩模,如Sobel滤波器掩模,从灰度图像中计算这些偏导数。所以这不是什么新东西,可以很容易地完成。关于时间方向的灰度值函数的偏导数也很容易计算。我们可以通过比较后续图像中的灰度值与当前图像中的灰度值(都在所关注的位置上进行评估)来近似计算它。这个近似给出了这个偏导数的近似值。因此,我们只需要灰度值信息来计算这些偏导数。从一对图像中,我们获得了一个以运动约束方程形式的约束,其中有未知的Delta U和Delta V。因此,从一对图像中,我们得到一个约束。
让我们看一下运动约束方程的简单示例。为此,我们将分析一个一维信号,即图像的一行,其中整个光流是向左或向右移动的,由一维向量Delta U表示。假设我们有一个用青色表示的灰度值函数,对于较小的U值有较小的值,对于较大的U值有较大的灰度值。我们要分析的是位于虚线所示位置U处的光流。我们假设在后续图像中,我们有相同类型的灰度值斜坡,但向右移动了一定的距离。后续图像的新灰度值函数由蓝色曲线表示。
一维信号的图示:
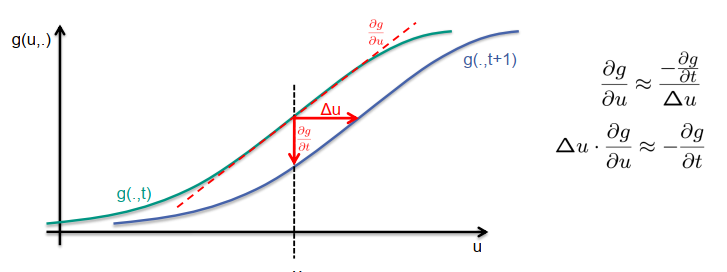
我们正在寻找的光流代表了向右的移动,如这个水平向量所示。对于时间方向的偏导数测量了感兴趣位置U的灰度值函数的变化。在这种情况下,我们可以观察到灰度值已经减小,因此这个偏导数可以用指向下方的垂直箭头来表示,与坐标轴相反。因此,这个导数的值是负数。
此外,我们知道,对于空间方向U,灰度级梯度可以被解释为感兴趣位置的灰度值函数的斜率。可以从灰度值函数的切线绘制的虚线红线来测量斜率,如此处所示。通过将这个虚线红线移动到垂直箭头的末端,我们可以观察到在灰度值遵循线性逼近的最佳情况下,我们得到一个三角形。这个三角形可以用来计算切线的斜率,该斜率大约等于垂直箭头长度与水平箭头长度的比值。由于垂直箭头向下指向,与坐标轴相反,我们需要添加一个负号来表示这个导数的负值。这给出了右侧所示的方程。如果我们将两边都乘以Delta U,我们就得到了一维情况下的运动约束方程。
运动约束方程:
这种方法可以直接扩展到二维情况。然而,有一个重要的区别。在一维信号的情况下,我们可以很容易地通过解方程相对于Delta U来计算Delta U,并获得Delta U的估计值。在二维情况下,这是不可能的,因为一个方程不能为两个未知变量提供解。
那么,我们该如何解决这个问题呢?关键是添加额外的方程,以获得两个未知变量Delta U和Delta V的多个方程。为此,我们假设光流在相邻点之间没有显著变化。我们假设右侧和左侧相邻像素的光流,以及上方、下方或对角线相邻像素的光流完全相同。通过为每个相邻像素计算一个运动约束方程,我们可以创建一个具有多个方程和两个未知数的线性方程组。
\[-\frac{\partial g}{\partial t}=\Delta u \cdot \frac{\partial g}{\partial u}+\Delta v \cdot \frac{\partial g}{\partial v}\]– 问题:一个方程,两个未知变量 – 附加假设:光流在局部环境中是恒定的。
\[\begin{aligned} -\frac{\partial g(u, v, t)}{\partial t} & \approx \Delta u \cdot \frac{\partial g(u, v, t)}{\partial u}+\Delta v \cdot \frac{\partial g(u, v, t)}{\partial v} \\ -\frac{\partial g(u-1, v, t)}{\partial t} & \approx \Delta u \cdot \frac{\partial g(u-1, v, t)}{\partial u}+\Delta v \cdot \frac{\partial g(u-1, v, t)}{\partial v} \\ -\frac{\partial g(u+1, v, t)}{\partial t} & \approx \Delta u \cdot \frac{\partial g(u+1, v, t)}{\partial u}+\Delta v \cdot \frac{\partial g(u+1, v, t)}{\partial v} \\ -\frac{\partial g(u, v-1, t)}{\partial t} & \approx \Delta u \cdot \frac{\partial g(u, v-1, t)}{\partial u}+\Delta v \cdot \frac{\partial g(u, v-1, t)}{\partial v} \\ -\frac{\partial g(u, v+1, t)}{\partial t} & \approx \Delta u \cdot \frac{\partial g(u, v+1, t)}{\partial u}+\Delta v \cdot \frac{\partial g(u, v+1, t)}{\partial v} \end{aligned}\]Lucas-Kanade Method 卢卡斯-卡纳德方法
在计算机视觉中,卢卡斯-卡纳德方法是一种广泛使用的光流估计的差分方法,这个方法是由Bruce D. Lucas和Takeo Kanade发明的。它假设光流在像素点的邻域是一个常数,然后使用最小平方法对邻域中的所有像素点求解基本的光流方程
通过结合几个邻近像素点的信息,卢卡斯-卡纳德方法(简称为L-K方法)通常能够消除光流方程里的多义性。而且,与逐点计算的方法相比,L-K方法对图像噪声不敏感。不过,由于这是一种局部方法,所以在图像的均匀区域内部,L-K方法无法提供光流信息。
如果我们有确切的两个方程和两个未知数,我们可以希望从这些方程中获得唯一解。如果我们有多于两个方程,由于随机性引起的方程之间的冲突,很可能我们找不到任何解。然而,我们可以通过说明我们不需要找到Delta U和Delta V以使运动约束方程完全相等来克服这个问题。相反,我们希望找到尽可能多地满足方程的Delta U和Delta V,这可以通过最小化这些方程的残差平方和来实现。残差表示运动约束方程的左右两侧之间的差异。这种方法被称为计算某一点的光流的Lucas-Kanade方法。这种方法的思想是在感兴趣点周围的某个区域内最小化残差平方和,例如最近的3x3像素的正方形区域。
可以通过最小化二次误差来估计光流
\[\begin{aligned} \operatorname{minimize}_{\Delta u, \Delta v} \sum_{(i, j) \in\{-1,0,1\}^2}\left(\frac{\partial g(u+i, v+j, t)}{\partial t}\right. & +\Delta u \cdot \frac{\partial g(u+i, v+j, t)}{\partial u} \left.+\Delta v \cdot \frac{\partial g(u+i, v+j, t)}{\partial v}\right)^2 \end{aligned}\]解决这个优化问题后,我们获得了Delta U和Delta V。解决方案涉及计算要最小化的函数相对于两个未知变量Delta U和Delta V的偏导数。然后将这些导数置零,并解出所得到的方程组,得到一个2x2矩阵
左边乘以未知变量的向量Delta U和Delta V(表示光流向量),等于右边具有两个条目的向量。矩阵和右边的向量可以从灰度值梯度信息计算得出,因此不需要额外的信息。如果左侧的矩阵具有满秩,我们将得到该方程组的唯一解。
在推导后并置零:
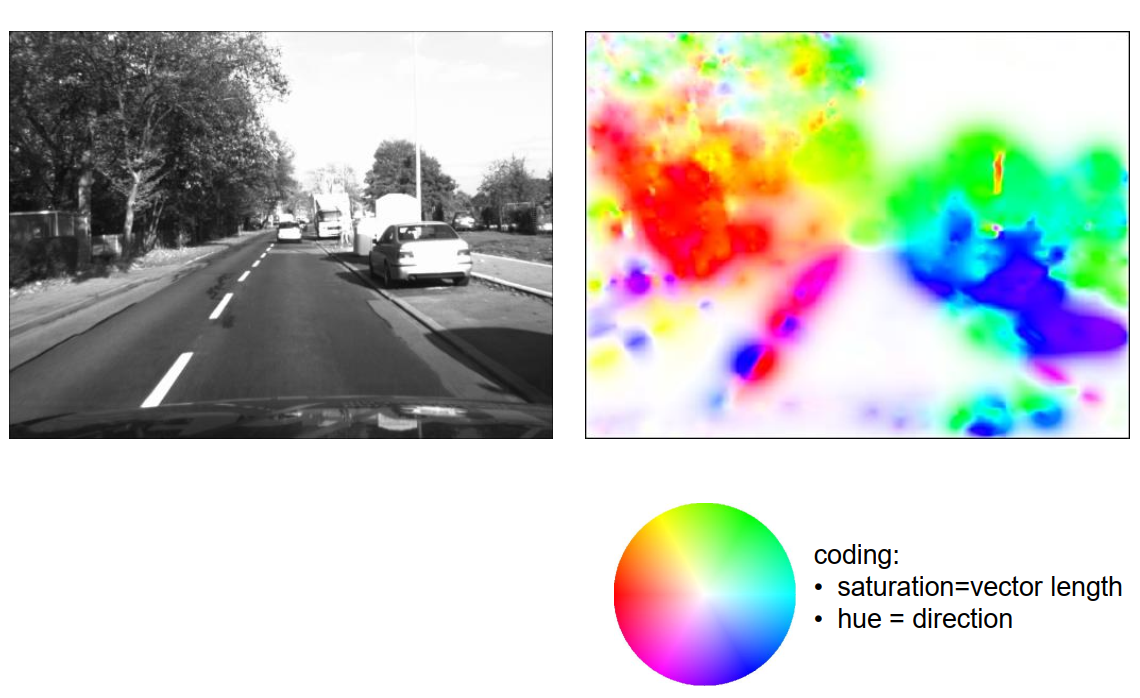
\[\begin{aligned} \left(\begin{array}{ll} G_{u u} & G_{u v} \\ G_{u v} & G_{v v} \end{array}\right)\left(\begin{array}{c} \Delta u \\ \Delta v \end{array}\right)=-\left(\begin{array}{l} G_{u t} \\ G_{v t} \end{array}\right) \quad \text { with } G_{u u} & =\sum\left(\frac{\partial g(u+i, v+j, t)}{\partial u}\right)^2 \\ G_{u v} & =\sum\left(\frac{\partial g(u+i, v+j, t) \partial g(u+i, v+j, t)}{\partial v}\right) \\ G_{v v} & =\sum\left(\frac{\partial g(u+i, v+j, t)}{\partial v}\right)^2 \\ G_{u t} & =\sum\left(\frac{\partial g(u+i, v+j, t)}{\partial u} \frac{\partial g(u+i, v+j, t)}{\partial t}\right) \\ G_{v t} & =\sum\left(\frac{\partial g(u+i, v+j, t)}{\partial v} \frac{\partial g(u+i, v+j, t)}{\partial t}\right) \end{aligned}\]这里提供了Lucas-Kanade方法如何计算光流向量的示例。在左侧,我们看到输入图像,它看起来非常模糊。事实上,模糊性实际上有助于Lucas-Kanade方法找到一些光流向量。在右侧,我们看到了每个像素的计算光流,根据下方提供的彩色轮进行了颜色编码。光流为0的向量将由白色像素表示。彩色轮显示了向量指向的方向,以及它的长度。高饱和度的颜色对应于较长的向量,而较低饱和度的颜色表示较短的向量。U值(红色、绿色或蓝色)确定向量指向的方向。从可视化结果中,我们可以观察到获得了一些光流向量,但并不是对所有点都获得了光流向量。此外,并非所有计算出的光流向量都是合理的,例如左下角的绿色向量。
总的来说,Lucas-Kanade方法提供了一种通过制定和求解使用运动约束方程和最小化残差平方和的线性方程组来估计光流的方法。



编码:
- 饱和度(saturation)= 向量长度
- 色调(hue)= 方向
线性近似的极限
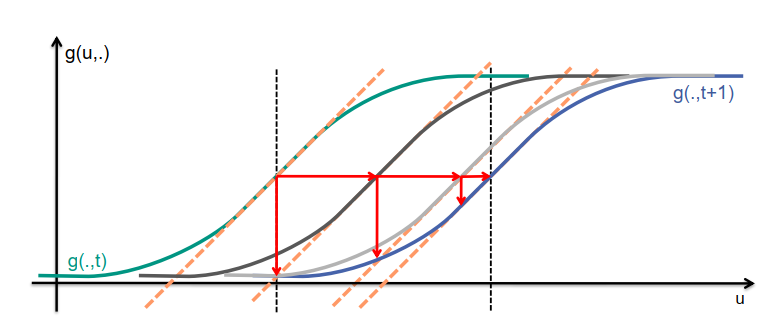
在所示的示例中,我们有一个一维灰度值图像,具有较大的移动,导致较长的光流向量。原始的灰度值函数由蓝色曲线表示,而后续图像的灰度值函数则显示为红色。
为了使用Lucas-Kanade方法计算光流,我们首先确定虚线橙色线所示位置的灰度值函数的斜率。我们计算随时间的灰度值变化(红色垂直箭头),并将切线线移到垂直箭头的顶部,得到移动的橙色线。连接原始位置和移动的橙色线的水平向量表示由Lucas-Kanade计算得到的光流向量。
然而,在这种情况下,光流向量显著低估了实际光流。为了解决这个问题,我们比较一下如果我们将原始灰度值函数向右移动光流量的话,灰度值函数会是什么样子。我们得到了黑色曲线,它与蓝色曲线或后续图像中的真实灰度值相差很大。
虽然存在很大差异,我们可以继续使用Lucas-Kanade方法计算光流,但基于黑色灰度值函数而不是原始的蓝色正弦曲线。我们迭代这个过程,计算灰度值差异并移动切线,以获得额外的光流估计。这些估计与先前计算得到的光流向量连接起来。
通过迭代执行Lucas-Kanade方法,我们可以获得比仅执行一次时更好的光流向量。这种迭代方法类似于使用牛顿法寻找函数零点。
线性近似不足以进行较大的偏移
– 也可以使用迭代计算(牛顿法)确定光流
图中展示了迭代的Lucas-Kanade方法的结果,其中光流向量与实际光流相比较之前的尝试更接近。



编码:
- 饱和度(saturation)= 向量长度
- 色调(hue)= 方向
Aperture Problem 光圈问题
除了可以使用迭代的Lucas Granada方法解决的问题外,还存在另一个问题,称为光圈问题(aperture problem),它会给Lucas Granada方法带来麻烦。让我们进行一个实验,假设有一个场景,我们只能通过百叶窗中的一个小孔来看到,这意味着整个场景可以被视为相机的镜头,百叶窗则可以被视为相机内部的百叶窗。因此,我们只能看到世界的一个小区域,在我们的实验中,我们感知到的这个小区域有一些白色背景和一些黑色物体,这些物体最初只出现在孔的左边界上。现在这个物体进行了一次移动,我们来看一下。
最后,物体以某种方式移动了,问题是我们观察到了哪种运动?显然,物体似乎是从左向右移动的,但这是完整的事实吗?我们能够唯一确定这个运动吗?
为了回答这个问题,让我们看一下百叶窗的背面,看看实际发生了什么。
在这里,我们可以看到我们实验的初始情况。现在我们开始这个运动,我们可以看到这个运动不仅仅是从左到右,而是沿着对角线方向的运动,因此还涉及到垂直运动,这是我们在示例中无法看到的。这个例子表明,我们可以感知到运动的部分,但无法完全感知到整个运动,在某些情况下。让我们稍微改变一下我们的例子,在这个例子中,我们改变了我们看到的物体的形状,现在我们再次进行运动,我们清楚地看到这是一个沿对角线方向的运动。因此,虽然场景只稍微改变,但完整的运动变得明显起来,那么这两个例子之间的区别是什么?在第一个例子中,我们只能观察到一个灰度值的边缘,而在第二个例子中,我们可以观察到一个灰度值的角落,这就产生了重要的区别。如果我们能观察到一个角落,我们就能确定完整的运动,如果我们只能观察到一个边缘,我们只能观察到运动的部分。
我们看到什么样的运动?



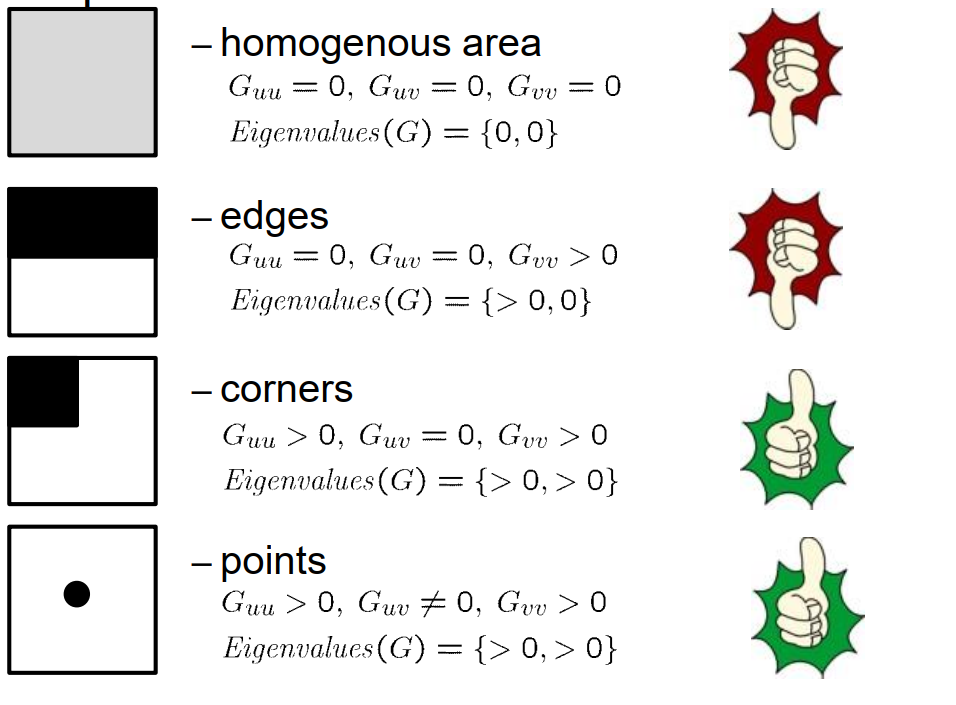
那么什么情况下可以解决Lucas-Kanade方法呢? 如果我们观察公式,我们可以看到涉及一个2x2矩阵,其中包含一些偏导数。当矩阵G具有满秩时,我们可以得到线性方程组的唯一解。 如果它的秩只有1,我们可能得到一组解,也就是说我们没有唯一解; 如果这个矩阵的秩为零,那么所有可能的向量或光流向量都满足这个矩阵,这意味着所有向量都能解决这个方程,我们就无法得到Lucas-Kanade的唯一解。 重要的性质是矩阵G具有满秩,因此它是可逆的。 如果满足条件,我们就能得到唯一解。这适用于当这个矩阵的两个特征值都大于零且远大于零时。
需要强调的是,这种矩阵始终具有两个实特征值,并且它们都是非负的,但重要的是它们不等于零,也不接近零,而是远离零。如果这两个特征值都满足条件,那么矩阵G是可逆的,并且这种反转也对相机图像中的随机影响具有稳定性。
\[\begin{aligned} & \underbrace{\left(\begin{array}{ll} G_{u u} & G_{u v} \\ G_{u v} & G_{v v} \end{array}\right)}_{=: G}\left(\begin{array}{c} \Delta u \\ \Delta v \end{array}\right)=-\left(\begin{array}{l} G_{u t} \\ G_{v t} \end{array}\right) \\ & G_{u u}=\sum\left(\frac{\partial g(u+i, v+j, t)}{\partial u}\right)^2 \\ & G_{u v}=\sum\left(\frac{\partial g(u+i, v+j, t)}{\partial u} \frac{\partial g(u+i, v+j, t)}{\partial v}\right) \\ & G_{v v}=\sum\left(\frac{\partial g(u+i, v+j, t)}{\partial v}\right)^2 \end{aligned}\]- 矩阵 G 是可逆的
- G 的特征值都近似相等且 > 0
那么什么情况下会发生这种情况呢?
-
如果我们观察均匀区域,我们会发现矩阵G的元素几乎都等于零,如果它们都等于零,特征值将是0和0,这意味着我们无法得到唯一解,这是一个糟糕的情况。
-
另一个糟糕的情况是灰度边缘,无论是水平还是垂直的边缘,在这种情况下,矩阵G有两个特征值,其中一个是零或接近零,另一个与零不同,对于所有灰度边缘(包括对角线边缘等),都是如此。 这也是我们无法得到Lucas-Kanade方法唯一解的情况。然而,正如我们所见,该方法仍然能够揭示关于运动的一些信息,但不是全部信息。
-
在灰度角点的情况下,我们通常会得到两个不为零的特征值,因此这是一个好的情况。
-
同样地,如果我们处理孤立点,我们会得到与零不同的特征值,所以这也是一个好的情况。这个思想类似于Stephen Harris角点检测器,并且在位移计算中也可以找到。基本思想仍然是相同的。
Variational Approach 变分法
由于我们面临着获取满秩矩阵G的问题,我们可能会问,我们计算矩阵G时应该考虑多大的环境范围。 我们只应该考虑像素感兴趣的直接邻居,还是应该考虑间接邻居? 我们应该考虑多少像素?我们可以一般性地增加环境的面积,也可以减小它。 那么最好的做法是什么呢?如果我们选择一个非常小的环境,很明显,我们很可能遇到我们刚刚看到的问题,也就是所谓的光圈问题。在这种情况下,矩阵G的秩不满,我们无法得到唯一解,因为环境中没有足够的纹理、结构,这使我们无法观察到完整的运动。
因此,我们可能会提出这样的问题:为什么不使用较大的环境来计算这个大写字母G呢? 然而,如果我们选择一个非常大的环境,我们可能会遇到其他问题。 当然,环境越大,我们需要进行所有计算的计算时间就越长。 更重要的是,如果我们选择了大的环境,我们可能会将不同物体的运动混淆在一起,因为在大的环境中,很可能我们不只观察到一个单独的物体,而是可能观察到几个不同的物体,它们以不同的方式运动。 因此,我们计算出的是几个物体不同运动方式的混合。
因此,这两种选择都不是最佳的,我们可能需要在这两个思想之间做出一些平衡。
这些方法的优点是我们可以获得几乎所有图像像素的光流向量。然而,缺点是需要大量计算来解决这些大规模优化问题,因此无法实时运行,只适用于批量处理记录的图像。这些方法更适合于批量处理记录的图像。

霍恩和肖克最初的方法奠定了变分方法的基础。
变分方法:假设光流在相邻像素中相似。
在变分方法中,基本思想是根据环境的特性进行自适应选择。如果处于均匀区域,可能需要选择较大的环境;如果处于纹理丰富的区域,可能更倾向于选择较小的环境。这是一种基本的思路,如何表达这个思想并使其更加普适呢?
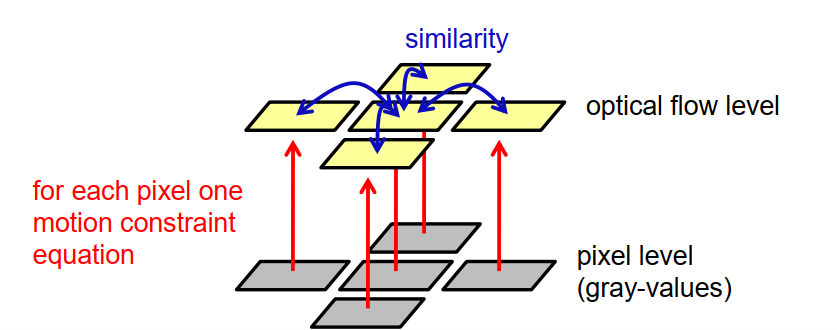
早在上世纪80年代,Horn和Schunck提出了一套基于变分方法的光流计算方法,后来的一系列方法都是基于这个思路。这些方法的基本思想是,不是单独估计每个点或单个点的光流向量,而是并行估计所有像素点的光流向量,并建立一个大规模的优化问题,将相邻像素的光流向量之间建立关系。通过这种方式,避免了对环境的特定选择,使其更加灵活。
具体来说,假设我们有一幅灰度图像,包含一组像素点。对于每个像素点,我们可以推导出运动约束方程,该方程建立了像素点的灰度值和光流向量之间的关系。我们假设相邻像素的光流向量是相似的,它们可能是相等的,或者至少在像素之间变化不大。我们通过一个条件来表达这种相似性,即希望相邻像素的光流向量之间的差异接近于零。
现在,我们有了一组从运动约束方程得出的条件,以及确定相邻光流向量相似性的条件。我们可以基于这些条件建立一个大规模的优化问题,然后使用数值方法来解决这个优化问题,以并行地找到所有像素点的光流向量。这里不详细介绍具体的方法,只是介绍了这个基本思路。
这些方法的优点是可以为几乎所有像素点计算光流向量,缺点是需要大量计算来解决这些大规模的优化问题,因此无法实时工作,只适用于批量处理记录的图像或视频。
如果想了解更详细的信息,请参考提供的参考文献,其中介绍了变分方法在光流计算中的基本原理和扩展。当然,Horn和Schunck的方法已经不再是最新技术,现在有许多对这种方法进行了改进并获得更好结果的扩展方法。不过,让我们先看一下Horn和Schunck方法的结果,以了解这些变分方法的工作原理。
然而,当今已经有很多对这种方法的扩展,比基本的霍恩和肖克方法表现更好。 不过,让我们看一下霍恩和肖克的结果,以了解这些变分方法是如何工作的。 我们从之前使用卢卡斯-卡纳达方法的示例开始,然后应用霍恩和肖克的方法,经过长时间的计算后,我们得到下面的结果。
我们可以看到,现在光流向量的估计比之前要好得多,尽管仍然存在一些估计错误和箭头状的伪影,但整体估计效果更好。我们还可以看到,平均光流向量的长度比卢卡斯-卡纳达方法更大,并且相邻像素更可能具有相似的光流向量,因为这是变分方法中引入的内容。
基于变分方法的解决方案:
- 变分优化问题,类似于随机场
- 数值迭代计算
- 无法实时运行!
- 有关详细信息,请参考提供的参考资料
Optical Flow and Stereo Vision 光流和立体视觉
光流计算 ≈ 立体视觉的对应问题
总结一下光流计算,我们已经了解了一些光流计算方法。 在之前的章节中,我们介绍了双目视觉,在双目视觉中,我们也面临着类似的问题,即我们想计算两幅图像中某个点的像素位置之间的关系,因此我们有了对应问题。
虽然光流计算与双目重建不同,但我们仍然可以认为这两个问题之间存在密切的联系。 在光流问题中,我们比较图像序列中的图像,而在双目视觉中,我们比较立体图像对。 在光流计算中,我们希望获得两个对应点之间的矢量,而在双目视觉中,我们希望计算视差,也可以将其解释为矢量。
因此,我们确定了一些可能的方法。
例如,可以使用运动约束方程进行光流计算,但如果需要的话,也可以用于双目重建。 变分方法主要用于光流计算,但也有非常类似的变分方法用于立体重建。 极线几何是在双目视觉背景下引入的概念,但也可以用于光流计算。 块匹配也是用于双目重建的方法,但也可以用于光流计算。 当然,特征点方法也可用于两个问题,至少可以用于获取稀疏光流或稀疏视差。
可能的方法(适用于两者)包括:
- 运动约束方程
- 变分方法
- 极线几何
- 块匹配/相关过程
- 特征点方法
稀疏流
为了说明特征点方法的有用性,这里有一个标准图像序列的示例。我使用SURF特征点为两幅图像创建了特征点,并连接那些相互匹配的特征点对。结果如下图所示,每条黄线表示一个光流矢量,我们可以看到大多数光流矢量是有意义的。当然,右上角存在一些特征点连接不合理的伪影,导致了一些奇怪的光流,我们并不期望这种情况发生。当然,汽车部分也产生了一些奇怪的光流,这也是我们所预期的。然而,总体结果还是相当不错的。当然,这只是对于光流的稀疏估计,我们并没有获得每个像素的光流,但至少对于那些获得光流的像素,结果还是相当好的。
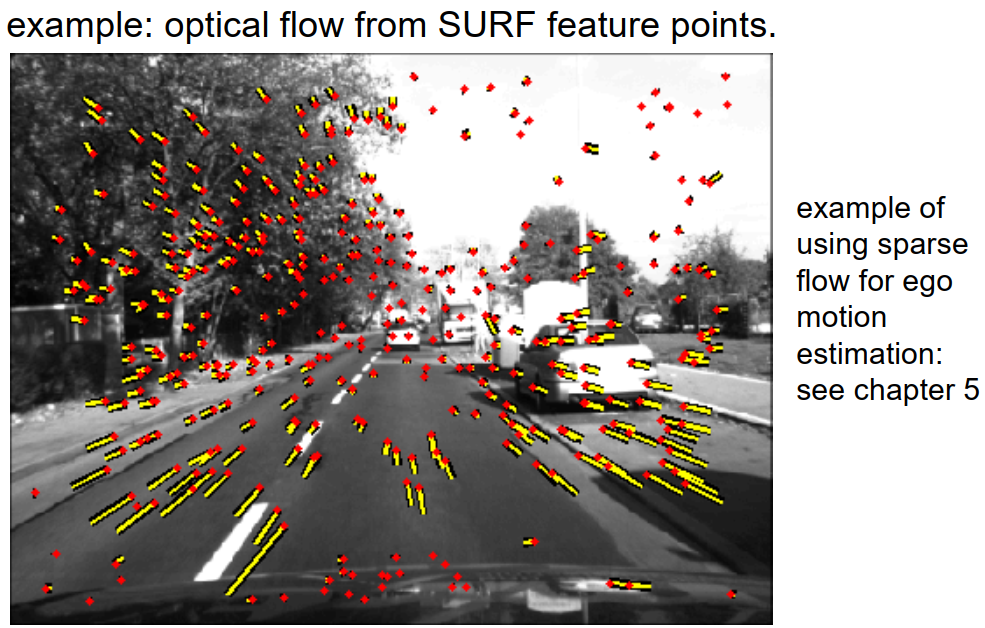
Image Based Tracking 基于图像的跟踪
在许多应用中,不需要计算每个像素的光流矢量,而是只对跟踪物体感兴趣,也就是确定属于某个特定物体的像素的光流。我们希望为整个物体获取一个单一的光流矢量。我们假设我们使用某种物体检测器,在第一帧中提供了一个感兴趣区域(ROI)。基于此,我们希望在整个视频序列中跟踪这个区域。我们假设我们不知道当前检测到的是什么物体,可能是汽车、人或动物等,我们只是想能够在整个视频中跟踪这个物体。

这里有一个例子,仅包含了一系列图像中的四个图像。我们可以看到几个物体。假设在第一幅图像中,物体检测器给出了三个感兴趣区域,用红色、绿色和蓝色矩形表示。我们的任务是在随后的图像中再次找到这些物体,并确定相应的感兴趣区域。
 解决这个问题的基本思路如下:
解决这个问题的基本思路如下:

从第一幅图像中,我们获取了对感兴趣物体的一些信息,即我们对物体的外观有一些概念。我们可以将这个外观作为该物体的模板,即我们只需将图像中的这个矩形区域作为模板。
然后在下一幅图像中,我们可以搜索相同的模板出现的位置。我们将该区域在整个图像上进行移动,对于每个位置,我们检查模板是否与图像中所见的内容匹配,并确定相似度的度量。在这种情况下,我们可能发现在这里显示的第一个区域的左侧区域不匹配,因此模板与该区域的内容的相似度非常低,而在右侧的另一个模板中,模板与图像内容的相似度相对较高。我们可以将其视为一种块匹配,再次比较图像的感兴趣区域的灰度值,并尝试找到最佳匹配。一旦我们找到了最佳匹配,我们就知道这个物体在第二幅图像中最有可能再次出现的位置。
现在,我们可以利用这第二幅图像,因为我们知道同一物体在第二幅图像中的位置,我们可以得到显示相同物体(或至少可能是相同物体)的第二个感兴趣区域。现在,我们可以使用第一幅图像和第二幅图像的两个感兴趣区域,并以最佳方式调整模板,使其适应两者。
这样就得到了一个适应的模板。有了这个适应的模板,我们可以进入第三幅图像,并根据最佳匹配搜索第三幅图像中最合适的区域。基于这个最佳匹配,我们可以再次调整模板以适应新找到的感兴趣区域的外观。
通过这样的步骤,我们可以逐步变得越来越好,以确定代表这种物体的良好模板。
基于图像的跟踪:超越块匹配 Beyond Block Matching
因此,创建模板并将其与图像块进行比较的方法既可以视为一种块匹配,也可以以不同的方式处理,并将其解释为分类任务。也就是说,我们想要搜索特定类别的物体,这些分类器通常使用一些示例图像进行训练。
在我们的情况下,我们从一个正例图像开始,即来自图像序列中的第一幅图像的感兴趣区域,然后我们选择一些其他图像块作为负例。一旦我们在第二幅图像中找到了感兴趣区域,我们可以将第二幅图像中的感兴趣区域视为第二个训练示例,用于训练专门针对相关对象类别的分类器,通过这种方式我们可以不断进行下去。
因此,我们对模板匹配使用可训练的分类器。参加过机器视觉或相关模式识别讲座的人可能已经对我们可以使用哪些分类器有一些了解,例如人工神经网络、支持向量机、决策树等等。在我们这里,我们将坚持支持向量机的思想,但不使用纯粹的支持向量机,而是经过改进的某种机器。
Example: Kernelized Correlation Filter (KCF) 核化相关滤波器 (KCF)
这导致了一种被称为核化相关滤波器的方法。相关滤波器让我们想起了块匹配方法,而核化则提醒我们支持向量机的思想,因为这些方法的基本思想是将一种块匹配与核化相结合。
在这种情况下,训练示例的创建如下所示:

假设我们在最初的图像中的感兴趣区域显示了这个骑自行车的补丁,然后我们将这个补丁复制并填充整个平面。此外,我们创建了一种类似原始补丁大小的标签图像,这个标签图像的值介于0和1之间。中心点的值为1,在边界处的值为0,两者之间的值从1递减。然后我们创建一组训练示例,第一个示例是从原始图像补丁和相应的标签创建的,标签的值是标签图像中心处的值。然后,我们围绕原始图像补丁转动这个红色矩形,并以相同的方式转动用于确定相应训练示例标签的标签图像中的点。当然,标签不仅仅是0和1,这是纯粹分类任务的预期,而是介于0和1之间的实数。因此,这些标签在某种程度上告诉我们一个正确示例的级别,我们就是这样创建训练示例的。对于你所看到的红色矩形的每个位置,我们创建一个训练示例。之后,我们可能会在灰度图像或彩色图像上计算一些之前计算的特征,并将其应用于这些灰度图或者彩色图。
之后,我们可能会在灰度图像或彩色图像上计算一些特征,并将其应用于这些训练示例,而不是直接使用颜色或灰度值。之前参加过机器视觉讲座的人会了解到一些特征,例如HOG特征或LBP特征,这些特征也可以用来创建训练示例,而不是直接使用原始图像数据。
然后,我们应用一个分类器,它类似于支持向量机,但不完全是支持向量机。在我们的情况下,可以使用快速傅里叶变换以高效地进行训练,因此这种训练只需现代计算机上的10到20毫秒,可以实时进行。这样,我们就训练出了一个分类器,现在我们可以在下一幅图像中搜索适当的最佳匹配。在这种的情况下,也可以使用快速傅里叶变换来实现这一点,从而获得非常快速的响应时间。
Example: Tracking with Occlusions 使用遮挡进行跟踪
是的,我们在获取新图像时逐步更新模板。在这里,我们可以看到核化相关滤波方法的一个例子,它通过一种额外的技术扩展以处理遮挡。这是我们团队中Weitian的工作成果。让我们开始视频,我们可以看到这种方法跟踪了一个骑自行车的人,即使自行车被汽车遮挡,它仍然能够跟踪。这里的思路是分析物体的哪些部分仍然可见,然后在这个可见区域上初始化第二个核化相关滤波器,可见区域显示为绿色。

Example: Tracking in Fog 雾中跟踪
让我们看另一个示例视频,在右下方的图像中,你可以看到初始情况,绿色矩形定义了一开始提供的感兴趣区域,很难确定我们实际上正在跟踪的是什么。如果你看左上方的图像,也显示相同的图片,我们可以看到有些东西,但很难说那是什么,即使我们放大并查看右上方的图像,我们几乎无法确定我们真正看到了什么,只有一些与周围的雾有些不同的深灰色区域。然而,让我们启动这个核化相关滤波器来跟踪物体。
现在我们可以看到物体的真正是什么,即一辆汽车。然而,从第一幅图像来看,几乎不可能确定这确实是一辆车,因此在第一幅图像中,车辆检测器无法确定这是一辆车,但我们仍然能够跟踪它,这真的很有趣。

总结一下光流计算和基于图像的跟踪这一章节。我们开始讨论光流,介绍了光流的基本概念,推导了运动约束方程,并基于此引入了Lucas-Kanade方法。然后,我们更详细地分析了Lucas-Kanade方法,推导了光圈问题,并介绍了变分流计算方法的一些基本思想。
对于基于图像的跟踪,我们引入了模板匹配的思想和核化相关滤波器作为一种有用且实时可行的方法来实现这种模板匹配思想,用于真实图像序列。
