chapter 2 Binocular Vision
双目视觉

欢迎来到《汽车视觉》第二章，今天我们将讨论双目视觉系统，也称为立体视觉。这是一些提供有关双目视觉系统章节的教科书列表。如果你需要超出本讲座范围的背景信息，请参考这些书籍以获取更多信息。让我们通过介绍对极几何概念来开始我们对双目视觉的讨论。

• R. Hartley, A. Zisserman, Multiple View Geometry in computer vision. Cambridge University Press, 2006
• E. R. Davies, Machine Vision. Theory. Algorithms. Practicalities. Elsevier, 2005, ch. 21.6 ff
• D. A. Forsyth, J. Ponce, Computer Vision. A Modern Approach. Prentice Hall, 2003, ch. 10
• R. Szilinsik, Computer Vision: Algorithms and Applications, 2010, ch. 10

Epipolar Geometry 对极几何

Binocular Vision / Stereo Vision 双目视觉/立体视觉

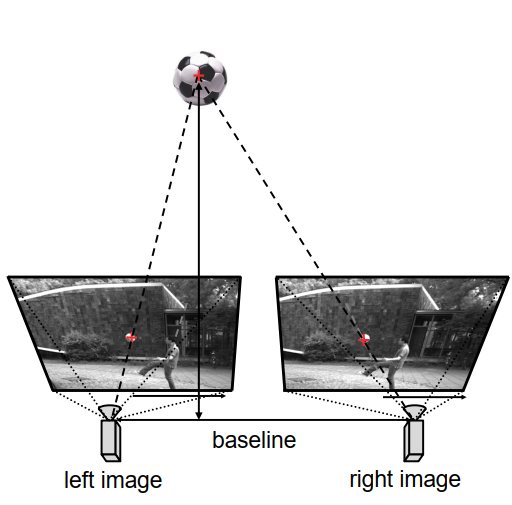
双目视觉或立体视觉系统由两个相机组成。每个相机将三维世界映射到二维图像上。当使用两个不同的相机从两个不同的视点观察同一场景时，我们会获得两幅图像。这意味着我们有一个从三维世界到二维（两倍）世界的映射，或者换句话说，从三维到四维世界的映射。这种映射使我们能够确定一个点相对于相机的距离，这是使用单个相机无法实现的。我们将这个距离称为点的深度。此外，我们将双目相机系统中两个相机之间的距离称为立体设置或立体摄像机的基线。

一旦我们确定了所有点的三维位置，我们就可以创建环境的三维模型。

• 场景是用两个摄像头拍摄的
• $\mathbb{R}^3 \rightarrow \mathbb{R}^2 \times \mathbb{R}^2$
• 3d 重建：确定到物体的距离（深度）

让我们从以下的图示开始分析：

我们有一个以焦点和图像平面为模型的相机。在现实中，相机的图像平面位于焦点后方。然而，为了简化分析，让我们引入一个位于相机前方的虚拟图像平面。由于针孔相机模型仅使用相机的焦点作为投影中心来实现透视映射，我们将在虚拟图像平面上观察到与在真实图像平面上相同的图像。然而，左右和上下是翻转的。此外，我们假设虚拟图像平面与相机之间的距离为1。

如果我们观察一个三维点P，我们可以通过连接这个点P与相机的焦点来构建一个视线。该视线与图像平面的交点将给出该点的图像点，我们在这个图示中将其表示为$q_l$。

这里所示的点$F_l$和图像平面描述了左侧相机。

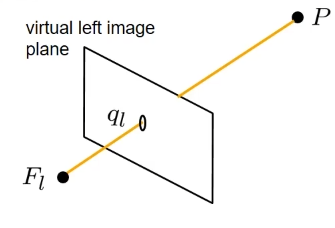
现在，让我们引入立体摄像机设置中的右侧相机，它也由其焦点和虚拟右图像平面定义。

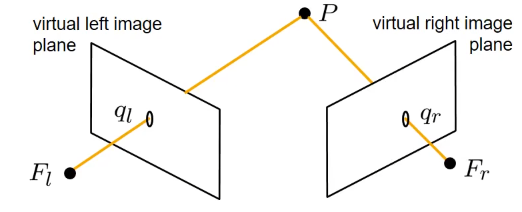
我们添加了第三条连接两个焦点的线，实际上就是基线。我们观察到这个基线也与图像平面在两个点相交，我们将其表示为$e_l$和$e_r$，并将它们称为相机系统的epipolar。请注意，图像平面本身是一个无限延伸的平面。我们在相机中感知到的图像只是该平面内的一个小区域。因此，即使epipolar在图像之外，它仍然存在。

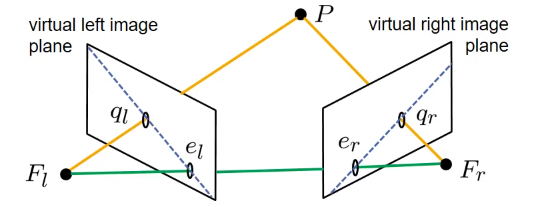
点$F_l$、$F_r$和$P$构成了一个三角形，这个三角形定义了一个平面，我们称之为极线平面（epipolar plane）。极线平面与虚拟图像平面在一条线上相交，这条线被称为相机设置的极线（epipolar line）。

在位于两个相机前方的极线平面上的所有点都会被映射到两个相机的图像平面上的极线上。

现在，我们可以基于这个模型进行计算，区分左侧相机和右侧相机的相关坐标系。我们引入大写索引’L’和’R’分别表示左侧和右侧相机的坐标系。在进行计算时，始终小心并检查我们当前所处的坐标系，因为混淆不同的坐标系可能会导致问题。

让我们首先建立起点P在左侧相机坐标系统中的三维位置描述向量PL与点P在左侧相机图像平面中的图像点位置描述向量ql之间的关系。从图示中，我们可以很容易地看出这两个向量只是彼此的缩放版本，缩放因子由$\frac{1}{z_l^L}$给出。这是因为虚拟图像平面与焦点之间的深度为1，而$z_l^L$是点P在左侧相机坐标系中的深度。因此，$z_l^L$只是向量$\vec{p}_l^L$的第三个分量。

类似地，我们可以对右侧相机坐标系和向量$\vec{p}_r^R$应用相同的推理过程。

此外，我们观察到点$F_l$、$F_r$和$P$构成了极线平面，而向量$\overrightarrow{p_l}$、$\overrightarrow{p_r}$和$\overrightarrow{b}$是极线平面的一部分。这意味着如果我们计算这些向量中任意两个的叉乘，我们将得到一个垂直于该平面的向量。此外，如果我们将这样一个垂直向量与平面上的其中一个向量进行点积运算，结果将为零。我们可以执行这个计算，例如，首先将基线向量$\vec{b}$与向量$\vec{p}_l$进行叉乘，然后计算与向量$\vec{p}_r$的点积。当然，我们必须确保所有这些计算都在同一个坐标系中进行，特别是左侧相机的坐标系。

• 左侧相机坐标系统： $\vec{q}_l^L=\frac{1}{z_l^L} \vec{p}_l^L$

• 右侧相机坐标系统： $\vec{q}_r^R=\frac{1}{z_r^R} \vec{p}_r^R$

• 假设向量位于一个平面上： $\left(\vec{p}_r^L\right)^T \cdot\left(\vec{b}^L \times \vec{p}_l^L\right)=0$

在我们之前的计算中，我们使用了向量$\vec{p}_r$，但是将其表示为左侧相机的坐标系，这有点不寻常。因此，让我们看看如何将其转换为在右侧相机坐标系中表示的向量。由于两个相机坐标系都是右手坐标系、正交坐标系，并且使用相同的长度单位，我们可以通过将这些点与幻灯片上表示的旋转矩阵（用大写字母$D$表示）相乘，并通过一定的偏移来将它们从一个坐标系转换到另一个坐标系。在这种情况下，偏移量是基线向量$\vec{b}$。现在，对于在左侧相机坐标系中表示的向量$\vec{p}_r$，它实际上是连接$\vec{F}_r$和$\vec{p}$的向量。这个向量可以被重写为从$F_r$到$F_l$，然后从$F_l$到$P$的组合。换句话说，它是从$F_l$到$P$的向量减去从$F_l$到$F_r$的向量。这两个向量表示了左侧相机坐标系中两个点的位置。现在，我们可以使用这个替换，应用上述的坐标变换规则，并将这些向量替换为在右侧相机坐标系中表示的相应向量。

在此之后，我们观察到项$\vec{b}^L$出现了两次，一次为正，一次为负，因此该项消失了。此外，我们可以将旋转矩阵$D$提取出来。括号中剩下的项实际上就是连接$F_l$和$P$的向量，表示在右侧摄像机坐标系中。这实际上就是$\vec{p}_r^R$。

结合我们之前的结果，我们可以得出以下结论： 旋转矩阵$D$乘以括号中的$\vec{p}_r^R$转置，再乘以$\vec{b}^L$和$\vec{p}_l^L$的叉乘，必须等于零。 *(下面式子最后一行)

• 坐标变换：$\vec{x}^L=D \vec{x}^R+\vec{b}^L$

现在，我们将这个结果与先前关于矢量ql和pl之间关系的结果相结合。我们已经得出这两个向量是通过一个缩放因子相关联的。现在，我们将这个关系代入以下方程中，将$\vec{p}_r^R$替换为$\vec{q}_r^R$，将$\vec{p}_l^L$替换为$\vec{q}_l^L$。 由于$z_r^R$和$z_l^L$（点在两个坐标系中的深度）始终是正数，我们可以将整个方程除以这两个深度值。我们得到下面的等式。

• 结合：

最后一步是将$\vec{b}^L$叉乘$\vec{q}_l^L$重新写成矩阵-向量乘法的形式。通过一些变换，我们可以将其重写为矩阵为3x3的矩阵乘以一个三维向量，如下所示。让我们将其表示为$\vec{b}^L$叉乘。可以在纸上试一下验证这个等式。

现在我们可以简化我们感兴趣的方程，最终结果为：$\vec{q}_r^R$的转置乘以E乘以$\vec{q}_l^L$等于零，其中E，也被称为本质矩阵 essential matrix，就是转置的旋转矩阵乘以矩阵BL叉乘。

很容易看出，本质矩阵只包含有关相机设置的内部参数的信息，也就是关于两个相机之间的相对位置的信息。

为什么这个结果如此重要呢？如果我们知道$\vec{q}_l^L$，也就是我们知道了左相机图像中的某个点，那么根据这个方程，我们可以确定右图像中的对极线。 因为右图像上的所有点都必须满足这个方程：$\left(\vec{x}^R\right)$的转置乘以E乘以$\vec{q}_l^L$必须等于零。所以这其实就是右相机图像平面上一条直线的定义。

类似地，如果我们知道右相机图像中的一个点，我们可以确定左相机图像中相应的对极线。

我们还可以确定立体摄像机系统的对极点，因为对极点是所有对极线共有的点。这意味着对于右相机的对极点，我们得到$\vec{e}_\tau^R$的转置乘以本质矩阵乘以$\vec{q}_l^L$必须对所有可能的$\vec{q}_l^L$值都相等。类似地，我们也可以得到左相机对极点的结果。

因此，如果我们想从立体摄像机系统中重建三维点，我们可以利用这一点。假设我们已经获得了立体摄像机系统的左图像和右图像，并且我们在左图像中找到了一个有趣的点QL。问题是，对应的右图像中的点在哪里？它可能在任何地方。

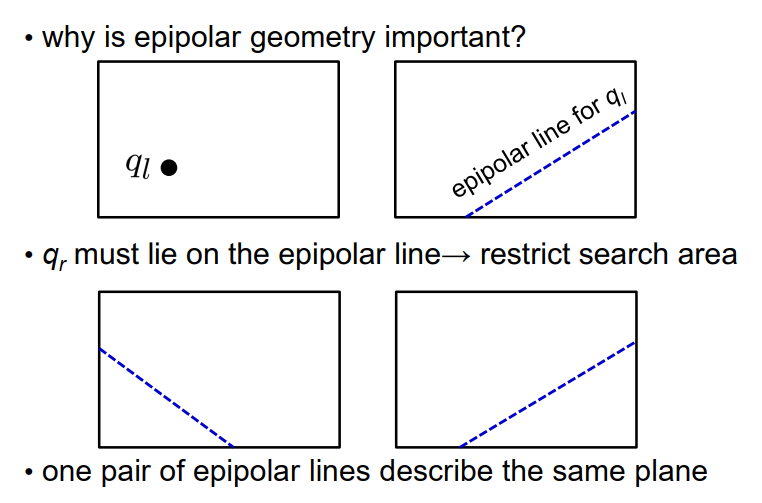
然而，如果我们知道了点$q_l$对应的对极线，我们就可以限制搜索范围，因为我们知道对应的点只能位于对极线上。这意味着知道对极线可以帮助我们将搜索空间限制在一维结构上，即一条一维线上。如果我们知道一对对极线，我们还可以确定对极平面。

Fundamental Matrix

在许多情况下，使用本质矩阵并不方便，因为如果我们想要使用图像坐标进行操作，通常希望使用图像坐标系统中的u和v坐标，而不是相机坐标系统中的坐标。为此，我们可以引入另一个矩阵，称为基础矩阵F，它实际上与本质矩阵相同，但使用图像坐标系统中的坐标。它可以通过将本质矩阵从左侧和右侧乘以两个相机的内部参数矩阵来导出，如方程中所示。

现在，我们之前针对本质矩阵导出的方程同样适用于基础矩阵。对于一对对应的图像坐标$u_l$、$v_l$和$u_r$、$v_r$，我们得到$u_r$、$v_r$、1乘以基础矩阵乘以$u_l$、$v_l$、1必须等于零。

基础矩阵可以从已标定的相机配置中导出，因为我们知道内部相机参数和外部参数，可以从中导出本质矩阵和基础矩阵。即使我们不知道这些内部和外部参数，如果我们有一定数量的左右相机图像上的对应点，仍然可以导出基础矩阵。如果我们至少知道八个点，我们可以使用所谓的八点算法估计基础矩阵F，但无法确定一个未知的比例因子。

• 在有基本矩阵 F 的情况下，首选图像坐标：
  • 具有内在相机参数的矩阵 $A_l$, $A_r$

• 在一对对应的图像坐标的情况下：

• 基本矩阵的形状可以通过一组≥8个对应的图像点（8点算法）直到一个未知的比例因子来计算。

例子

让我们来看一些例子。这里，我们看到两个图像显示的是同一个场景，但在左图中，视角稍微向左，而在右图中，视角稍微向右。我们看到一些蓝色的线，它们是极线，以及一些用小绿点标记的点集。在这些情况下，极线大致是水平的，并且极点远离图像之外。

– horizontal panning motion 水平平移运动

这张图片展示了类似的情况，但现在视角位置重叠。极线是垂直的。

– vertical panning motion 垂直平移运动

– horizontal and vertical panning motion 水平和垂直平移运动

这是一个情况，其中两个摄像机的视角在水平和垂直方向上发生了移动，因此极线有些倾斜，至少部分倾斜。最后，让我们来看一下摄像机不是向左、向右、向上或向下移动，而是向前或向后移动，离场景越来越近或越来越远的情况。在这种设置中，四个极点都位于图像内部，正如我们在所有极线的交点处所看到的，这些交点就是立体设置的极点。 – motion parallel to optical axis 平行于光轴的运动

此外，还有一个非常特殊的极线几何情况，即具有相同图像平面、相同内部参数的相机，且相机完全平行且方向相同。这种情况如图所示，两个摄像机只是平行于摄像机坐标系的x轴向左或向右移动。在这种情况下，极线是平行的且完全水平的。我们需要在另一个图像的同一行上搜索对应的点。极点位于无限远处。

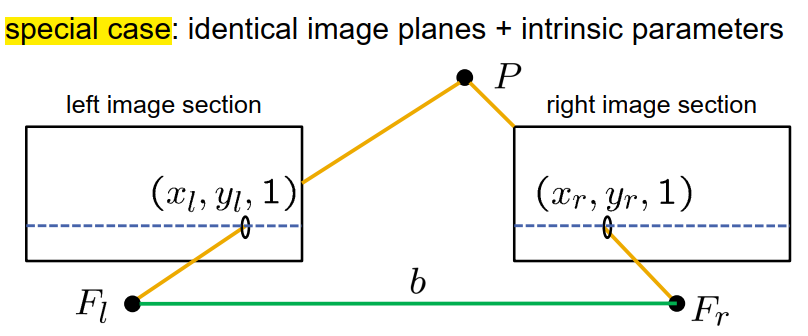
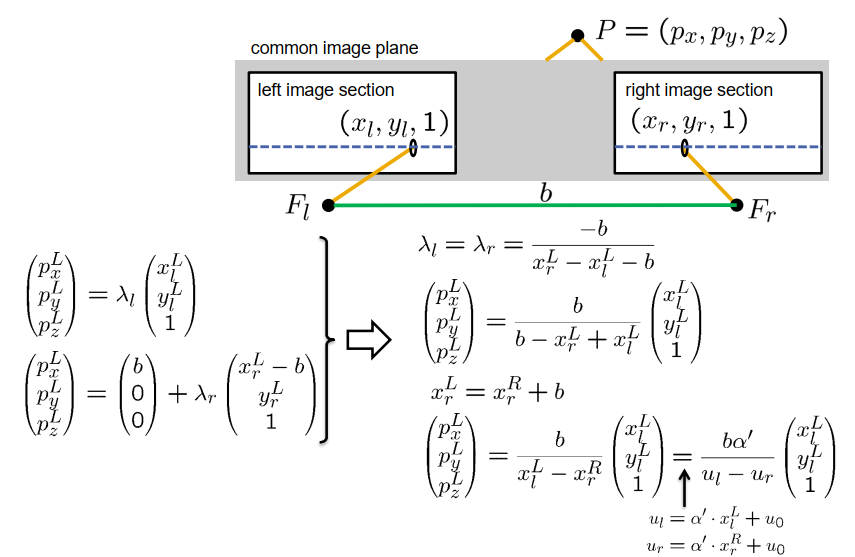
在这样的设置中，我们称之为矫正相机设置，计算特定点的深度相对容易。首先，我们需要确定该点的视差，即图像坐标中对应点的 u 坐标之差。因此，视差（表示为 Ddisparity）等于 $u_l$ 减去 $u_r$。这总是一个非负数。基于视差，我们可以轻松计算出点 $P$ 的三维位置。它由基线（两个焦点之间的距离）乘以 $\alpha^{\prime}$（相机设置的有效焦距）除以视差，再乘以向量 [$x_l^L$, $y_l^L$, 1] 给出。该向量表示左侧相机的焦点和相机坐标系中的图像点的位置。

• 视差（以像素为单位）：$d=u_l-u_r$
  

Derivation:

Disparity 视差

我们可以看到校正或矫正立体设置的视觉效果。在顶部，您可以看到立体摄像机的左图像和右图像，在底部，您可以看到两个图像一个接一个地显示。我们可以观察到，当图像发生变化时，所有的点都向左和向右移动，然而它们不上下移动。我们还可以进一步观察到，远离我们的点，例如背景中的房屋，移动得不多，即视差较小，而前景中的点，例如行人，移动得很多，这些点的视差很大。

Rectification 矫正

实际上，几乎不可能构建一个完全矫正的相机系统，因为我们在安装相机时所需的精度在机械上很难实现。那么，如果我们无法构建矫正相机，我们如何使用矫正相机呢？答案很简单，我们可以从实际的立体设置中创建虚拟矫正相机。这个原理在下面的图片中展示。我们从原始相机设置的图像开始。这个设置并不差，所以相机的对准尽可能好，但不完美。然后，我们进行一些转换，称为图像的矫正，然后稍微修改图像，使其完全矫正。

它是如何实现的？起点是我们有立体设置的两个相机，具有不同的相机参数Al和AR，以及不同的坐标系。我们的目标是定义两个新的虚拟相机，一个左虚拟相机和一个右虚拟相机，两者应该具有相同的焦距，以及相同的内部参数。

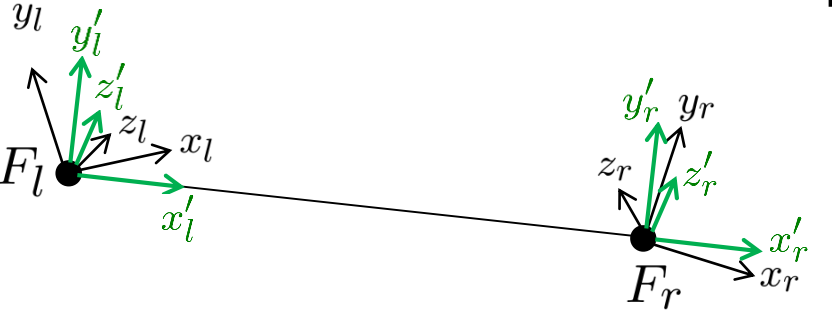
两个虚拟摄像机的对齐方式应该是完全一致的，这意味着它们的相机坐标系应该完全对齐。它们的相机坐标系的x轴应该与连接两个焦点的基线平行，并且焦点应该与原始摄像机的焦点相同。也就是说，左侧虚拟摄像机的焦点应与真实左侧摄像机的焦点相同，虚拟右侧摄像机的焦点应与真实右侧摄像机的焦点相同。

我们可以将这个过程可视化如下：我们从一个真实相机开始，你可以看到相机坐标系彼此不对齐。然后我们将它们旋转，使它们的x坐标与基线平行，而它们的y和z坐标也互相平行。然后我们忘记原始坐标系，只使用这个虚拟双目相机设置。我们如何计算这个呢？

首先，我们需要根据相机参数定义一个共同的内部矩阵$A^{\prime}$，这个矩阵类似于原始内部相机矩阵$A_l$和$A_r$。

其次，我们要找到一个共同的相机坐标系，使得x轴平行于基线。在定义这个坐标系时，我们有一定的自由度，因为我们可以始终围绕x轴旋转，并得到不同可能的矫正相机坐标系的选择。 实际上，我们在实践中使用尽可能与原始两个相机坐标系相似的坐标系。一旦我们定义了这些新的坐标系，我们确定所需的旋转矩阵，用于将原始坐标转换为新的坐标。 然后，我们将原始相机图像转换为虚拟相机的图像，也就是创建了新的虚拟矫正相机图像。

这可以按照以下方式完成：从透视投影中，我们知道如果我们知道点p在原始相机设置和左相机的坐标系中的3D点位置，通过将$A_l$与$\vec{p}$相乘，我们得到图像坐标。左侧的结果是深度pz乘以该点的图像坐标。我们可以对新的虚拟左相机系统进行类似的计算。对于新的虚拟相机坐标系，我们有P’×a’ = pz’×u’×b’，其中带有撇号的变量是与新的虚拟相机坐标系相关的变量，这个新坐标系中的点的深度和坐标都可能发生变化。

知道两个坐标系之间有一个已知的变换，仅由一个旋转矩阵定义，我们可以将点$\vec{p}^{\prime}$转换为$D_l$乘以$\vec{p}$。

现在我们可以合并这两个方程，并通过从上面的方程推导出的相应方程替换点P，最终我们得到了你在这里看到的术语。通过将整个方程除以$p_z$，我们得到一个简化的项目$\frac{p_z^{\prime}}{p_z}$，这只是一个缩放因子，我们可以通过这个方程的第三行确定缩放因子。一旦我们知道了缩放因子，我们就可以确定$u^{\prime}$和$v^{\prime}$。如果我们想根据实际图像中的位置确定虚拟图像中的点的位置，这意味着我们可以创建一个描述实际图像中的点如何映射到虚拟矫正图像中的点的映射。我们可以对左右两个虚拟相机都这样做，并最终得到结果。

最后，让我们分析从我们可以确定该点的视差的准确性来看，深度计算的灵敏度如何。

我们已经推导出深度$p_z$取决于视差$D$的公式，其中包括项基线$b$乘以有效焦距$\alpha^{\prime}$除以视差$d$。如果我们假设我们只能确定视差到某个位置，那么我们假设在计算这个视差时会产生一定的误差$\varepsilon$。让我们考虑一下这个误差和视差计算对计算深度的影响有多大。为此，我们使用泰勒展开。对于视差$D$+ $\varepsilon$，我们可以近似为视差$D$ - $\varepsilon$ 的点的深度，其中深度对视差的一阶导数为$b$乘以$\alpha^{\prime}$除以$d$的平方。这可以表示为$D$ - $\varepsilon$ / $b$乘以$\alpha^{\prime}$乘以$z$平方，这意味着在深度估计中获得的误差与点的距离的平方成正比。也就是说，点离得越远，我们在深度估计中得到的误差就越大。

该图显示了这种误差增长的典型示例。现在我们清楚地看到在水平轴上是点的真实距离，而在垂直轴上是如果我们对视差进行了半个像素的小猜测或小测量所得到的误差。我们很容易看到误差的正确二次增长。

Correspondence Problem 对应问题

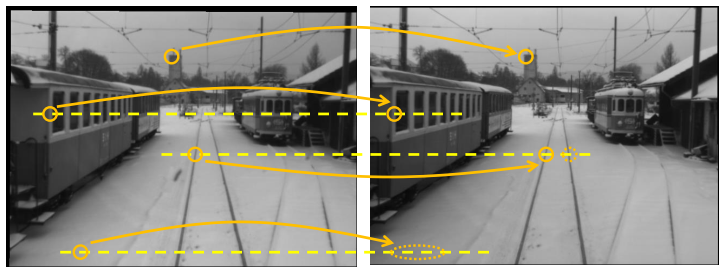
现在让我们来讨论对应问题。到目前为止，我们假设我们知道左图像中的哪些点和右图像中的哪些点表示三维世界中的同一点，但实际上这是未知的，我们需要计算它。我们来看一对经过矫正的立体图像。

在左图像中，一个点用橙色圆圈标出，它是建筑物的左上角。对于这个点，找到右图像中的对应点相对容易，因为这个点非常显著，我们可以比较容易地确定它。

对于第二个点，它位于一个窗户的垂直边缘上，情况稍微复杂一些。在右图像中，我们可以找到同样的垂直边缘，但是如果没有任何额外的信息，我们不会确切地知道这个边缘上的哪个点是对应点。幸运的是，在这种情况下，我们知道我们正在处理的是矫正的相机图像，这意味着我们知道我们必须在同一行中搜索，因为这是对应的极线。如果我们利用这个额外的知识，我们可以轻松找到对应点。

在第三种情况下，我们处理的是轨道上的一个点。同样，我们可以使用相同的技巧并利用极线，但不幸的是，在这条极线上有两个非常相似的点，两个轨道上的点都有可能是对应点。如果我们分析整个图像并理解整个图像，我们将能够轻松区分左侧的轨道和右侧的轨道。但如果我们只看局部区域并比较右图像中的哪个区域与左图像中的哪个区域相似，可能会遇到问题，因为在这种情况下，错误的对应点看起来比正确的对应点更相似。

最后，最糟糕的情况发生在雪地中的这个点。我们知道我们必须在极线上搜索，但不幸的是，图像中没有足够的结构来确定对应点的位置，我们只能说它必定在这个区域，但无法确定确切位置。

为了确定对应点，我们可以利用几个特性，特别是在矫正的图像中。如果图像是由相同类型的相机拍摄，并且曝光时间选择相同，那么点的灰度值应该是相同的。它们应该具有相同的局部环境，看起来非常相似。它们必须位于同一对极线上。这些点的邻域也应该大部分时间保持不变，这意味着如果我们在左图像中有两个点，一个在另一个点的左边，那么相应的右图像中的点的顺序也应该如此。正如我所说，有一些例外情况，不满足这些条件，但这些例外情况相当罕见。最后，在左图像中，U坐标大于右图像中的U坐标，因此视差始终是非负的。

对应的点：

• 具有相同的灰度值
• 具有相同的局部环境
• 位于同一对极线上
• 邻域被保留（大部分情况下）
• 在左图像中的u坐标大于在右图像中的u坐标（矫正后的图像）

Block Matching 块匹配

我们如何确定对应点呢？方法是比较两个点的局部环境，这就得到了一种称为块匹配的方法，因为我们比较的是灰度值的块。在这种情况下，我选择了左图像中的一个图像块，如顶部所示，并提供了三个可能的右图像中的候选点，它们可能是对应点。

现在我们可以比较这些图像块，看灰度值结构的相似程度，例如通过一个灰度值差异度量，我们可以得到左边的图像块的差异为74.9，中间的图像块的差异为43.8，右边的图像块的差异为3.2。在这种情况下，我们只是计算了逐像素的绝对灰度值差异，然后取平均值。当然，我们还可以选择其他灰度值差异度量的方法，例如如果我们喜欢，我们可以选择平方差异而不是计算绝对差异。在这种情况下，我们将得到这些值。最后，我们会选择最相似的图像块，也就是具有最小差异的图像块，并将其选为最有可能的对应点。

数学上，我们会检查以左图像中感兴趣像素 $u_l$、$v_l$ 为中心的一定区域，并分析通过该区域中的所有像素的灰度值结构，使用两个运行索引 i 和 j。

对于右图像中的潜在对应点，我们也会考虑相同区域内的所有像素，并逐像素比较灰度值，取绝对差异并对所有像素求和。如果需要，我们可以通过将结果除以该区域中的像素数量来取平均值。这将得到灰度值绝对差异的总和。对于平方差异，计算方式非常类似，只是在差异的计算中取差值的平方。另一个选项是使用相关性，如此处所示。该相关性是从统计学上确定的，具有一些不同的特性。前两种度量方式，如果图像非常相似，它们会很小；相关性在两个图像相似时很大；它们在两个图像完全相同时达到最大值 1；而当它们非常不相似时，相关性为 -1。

相关性具有一些优势，因为它对消除具有不变性。如果两个图像块通常稍微亮或暗一些，相关性对这些变化不敏感，例如由于相机的曝光时间不同。然而，灰度值绝对差异和平方差异是不具有这种不变性的。

• 左图中像素 (ul,vl) 周围的局部环境：

• 左右分割段的区别：
  • 对灰度值绝对差求和：
    

• 对灰度值平方误差求和：
  

• 相关性:
  

让我们以一个例子来说明。 上方是我在左图像中选择的图像块，下方是右图像。 我们可以将此图像块与右图像中的所有可能像素进行比较，不考虑首先考虑极线几何关系。然后，对于每个像素，我们得到一个特定的误差项，如此处所示。颜色表示了右图像中相应像素周围区域的差异程度，蓝色表示差异小，非常相似，红色表示差异大，非常不同。如果我们寻找最小值，我们实际上会找到一个位置，如右图像中用红色矩形标示的位置，这是实际的对应点。

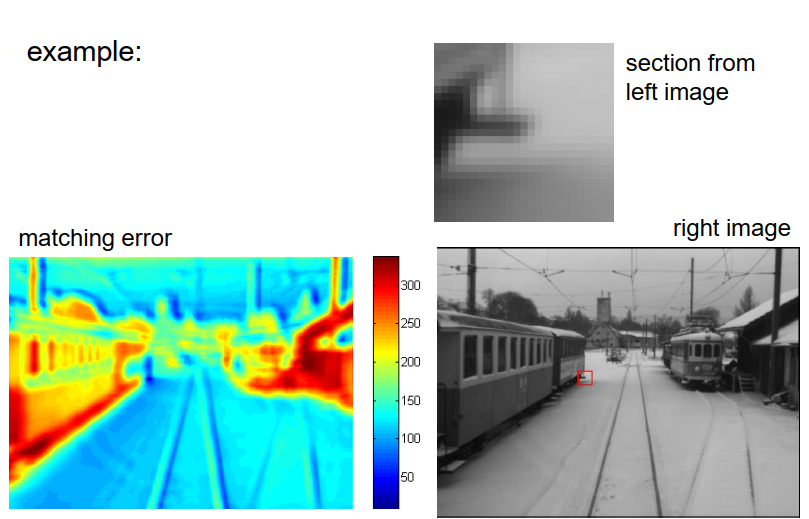
在实际应用中，我们对图像的所有像素进行这个过程，并当然使用了极线来限制搜索范围，只搜索相应的极线，以避免过多的计算。

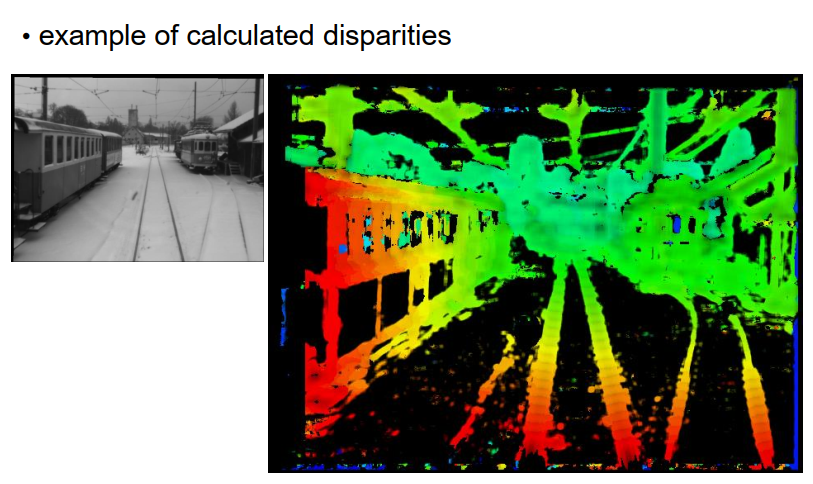
我们这样做会得到视差图像，你可以在右侧看到示例。这个视差图像显示了每个像素的视差值，视差值使用颜色编码，绿色表示小的视差，红色表示大的视差，对于黑色区域，我们无法确定视差，因为点周围的环境结构不足，没有足够的纹理来确定对应点，正如我们在这里看到的，尤其是在非常均匀的雪地区域，无法确定对应点。但对于铁轨、架空线缆、背景建筑或铁路车辆等场景，我们可以确定对应点。

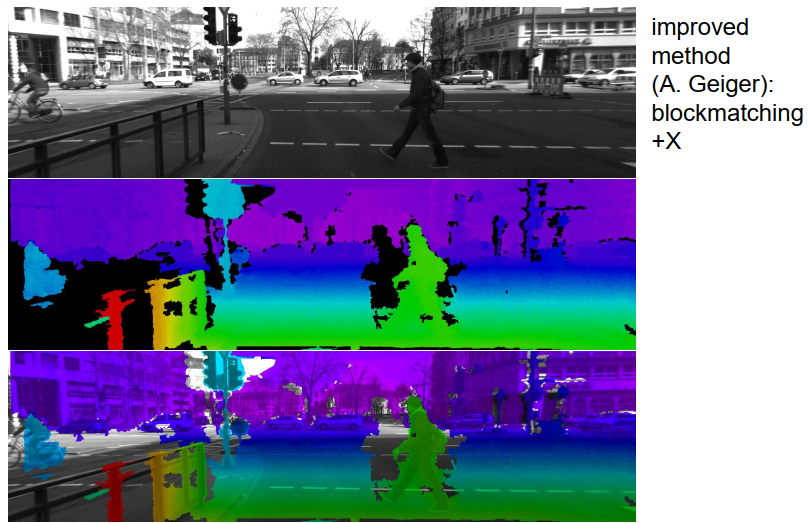
这里是另一个例子，展示了一位前博士生安德烈亚斯·盖格（Andreas Geiger）开发的块匹配方法，他添加了一些额外的技术来得到一些密集的视差图，如你在这里所见。可能有趣的是，在第二列的视差图中有一些黑色区域，看起来像是物体的阴影。例如，对于行人的背后，我们看到一个黑色的区域，无法计算出视差。在这种情况下，该区域的结构足够丰富以计算视差，但行人本身遮挡了其后面的一些区域。这些遮挡区域在左右相机中是不同的，因此对于在一个相机中被遮挡而在另一个相机中没有遮挡的点，我们显然无法计算出视差值，因此在这些区域中，我们得到这些视差阴影。

关于块匹配的一些说明

它是一种具有许多优点的方法，非常通用，可以用于很多应用，双目重建是其中一个可能的应用，但不是唯一的应用。光流计算，我们在第四章中讨论过的内容，是另一个应用。我们可以利用极线几何来限制搜索范围，但如果我们无法访问极线几何，我们也可以在整个图像上执行块匹配。

在使用块匹配时，存在一些不足之处。完整的搜索可能需要大量计算资源，尤其是对于大图像而言，因为它涉及对大量图像块进行比较。此外，只有当图像块中的灰度结构足够丰富时，才能明确地确定对应点。如果图像块的结构较差，存在找不到准确对应点的风险。

另一个考虑因素是我们在块匹配中比较的区域大小。如果区域太小，图像块中的灰度结构将较差，增加了错误匹配的风险。然而，如果区域太大，计算时间会增加，并且区域可能包含属于不同对象且具有不同深度的像素，这会增加错误结果的可能性。

在实践中，块匹配通常应用于预先校准的图像上，这样它们就不会受到整体照明条件的影响。为了避免由于左右图像的亮度差异（由于曝光时间不同或其他原因）而导致块匹配失败，许多研究人员首先对图像进行Sobel或Laplace运算，以获得一阶或二阶滤波图像，然后在梯度图像上应用块匹配。通过使用导数计算（如梯度），消除了整体亮度水平的影响，使整个过程对消除不变。