Chapter 6: Self-Localization and Mapping

欢迎回到汽车视觉的第六章，我们将讨论以相机为基础的自我定位和映射的主题。

自我定位和映射的主题是机器人技术和制图和地理信息学领域进行大量研究的领域。例如，在Tune Burger和Fox的《概率机器人》一书中，第七到十三章覆盖了这些主题。IEEE机器人与自动化杂志上的一篇分成几部分的同时定位和映射教程，由Duran、White和Bailey编写。你还可以在《机器人手册》中找到关于定位和映射的基础知识。

另外，如果你对涵盖这些主题的德语机器人书籍感兴趣，你可能会考虑Hartsback、Lingaman和Nishta的《移动机器人：信息科学导论》。第五和六章中你可以找到这些主题。最后，Cox在1991年撰写的一篇原创论文，描述了一种用于多种情况的算法，即最近迭代点算法，这也可能是一篇有趣的论文，以了解整个领域在1990年代初如何启动。

References

• Sebastian Thrun, Wolfram Burgard, Dieter Fox, Probabilistic Robotics. MIT Press, 2005, Chapter 7-13 (partly)
• Hugh Durrant-Whyte, Tim Bailey, Simultaneous Localization and Mapping: Part I, IEEE Robotics and Automation Magazine, 13(2), pg. 99-110, 2006
• Tim Bailey, Hugh Durrant-Whyte, Simultaneous Localization and Mapping: Part II, IEEE Robotics and Automation Magazine, 13(3), pg. 108-117, 2006
• Bruno Siciliano, Khatib Oussama (Hrsg.), Springer Handbook of Robotics, Springer, 2008, Chapter 37
• Joachim Hertzberg, Kai Lingemann, Andreas Nüchter, Mobile Roboter – Eine Einführung aus Sicht der Informatik, Springer 2012, Chapters 5+6
• Ingemar J. Cox, Blanche – an Experiment in Guidance and Navigation of an Autonomous Robot Vehicle. IEEE Transactions on Robots and Automation, 7(2), pg. 193-204, 1991

Self Localization 自定位

自我定位领域对许多不同的应用都很重要，其中之一就是自动驾驶，其他的还包括移动机器人或甚至制图。

在所有这些应用中，任务都可以通过三个元素来描述。第一个元素是环境的地图，我们假设我们知道那张地图。在这种情况下，地图总是数字地图，也就是存储环境中相关对象位置和几何形状的数据库。对于自动驾驶车辆，这些地图可能包含道路几何形状，道路旁边的相关对象的位置，比如树木、交通灯、交通标志或房屋。它可能包含车道标线的几何形状等等。我们不知道的，但我们想要估计的是车辆的位置和方向。这对位置和方向的配对通常被称为车辆的姿态。此外，我们假设车辆配备了能够识别本地环境元素的传感器。例如，摄像头可能识别到车道标线，或者激光雷达传感器可能识别到交通标志的柱子或树木。因此，我们想要做的是，我们想要使用这种本地感知，并以某种方式将其与地图结合起来，以确定车辆的姿态。

self localization problem 自定位问题：

• environment is known (map) 环境是已知的
• vehicle position and orientation are unkonown 车辆位置和方向未知
• vehicle observes the (local) environment 车辆观察（本地）环境

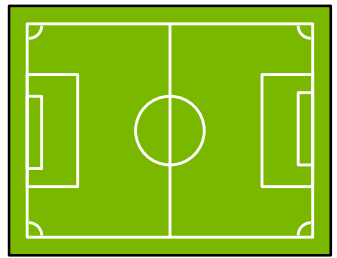
让我们从一个非常简单的例子开始，即足球机器人。假设你应该为一个移动机器人实现一个程序，使机器人能够踢足球。当然，对于足球机器人来说，知道它在球场上的位置，以及它在球场上的方向，是非常重要的。通常，我们知道足球场是什么样子的，我们知道球场的尺寸，我们知道球场的标线是怎么画的，所以我们可以创建一个精确描述这个场地外观的数字地图，在场地上我们找到哪些元素。假设机器人配备了一些传感器，比如一些摄像系统，感知机器人的本地环境。由这样的摄像机创建的可能的图像可以在右手边看到。所以，这展示了机器人的视角。我们可以看到足球场和场地标记，我们还可以看到其他一些对象，比如其他机器人或球之类的东西，这些对象是移动的，不是地图的一部分。

所以，现在的问题是，当我们考虑机器人的这种视角时，我们能否推断出机器人当前的位置和方向。当然，作为人类，我们可以很容易地看到，我们以某种方式正朝着足球场的一个角落看去，所以我们可以推断出，我们必须位于某个区域，以某种方向看向角落。此外，我们看到一部分罚球区的标记，所以我们可以推断出，机器人位于现在在足球场上可见的这两个位置中的一个。箭头指示机器人当前朝向的方向。

当然，在这种情况下，很明显有两个可能的位置，因为足球场是对称的，所以有时候我们不能确定位置，但我们仍然有几个可能的位置，机器人可能在那里，而且由于机器人的视野有限，我们不能解决这种歧义。但是，如果我们随着时间的推移跟踪自我位置，我们可能稍后能够找出我们目前位于哪个歧义的位置。所以让我们从最简单的方式开始这个自我定位的主题，即使用地标的定位。

Localization with landmarks 地标定位

landmarks 地标：

地标是什么呢？地标是环境中的一个物体，是静态的，不会移动，我们知道它的位置，所以它必须是地图的一部分，我们必须知道那个物体的位置。此外，地标应该在机器人或车辆使用的传感器中容易识别。当然，一个典型的地标就是早期用于船只自我定位的灯塔，它们清晰可见，易于识别，它们在世界上是静态的，可以通过船上的一些光学仪器来看到，这就是一个典型的地标示例。当然，我们并不是为船只做定位任务，而是为车辆或机器人做定位任务，但你可以为移动机器人或移动车辆的自我定位假设类似的事情。例如，在路上，你可能会找到一些物体，比如交通标志或交通灯，它们在世界上是静态的，一点也不动，很容易识别，可以用来进行自我定位。

现在，让我们假设我们正在处理一个二维问题，或者更准确地说，是在二维平面中自我定位的问题。

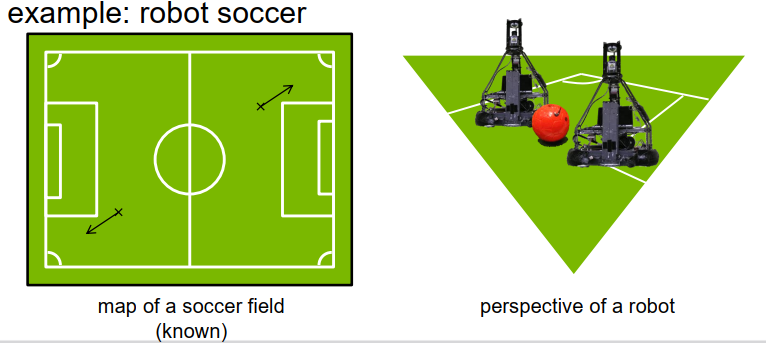
那么，当我们观察到其中一个地标时，我们能得出什么结论呢？首先，假设我们的传感器能够测量到地标的距离，当我们能够确定到地标的距离时，我们能够对机器人或车辆的位置得出什么结论呢？假设我们知道地标的位置，我们可以在地图上标记出来，这是中心的红色点。我们知道我们与地标的距离，也就是说，我们可以推断出机器人必须位于蓝色圆圈上，给定的距离为半径，所以这个圆圈描述了机器人可能的所有位置。当然，只知道距离不能确定方向。

假设我们正在观察两个地标，比如两个灯塔。

对于每一个灯塔或地标，我们确定距离，也就是说，我们可以创建两个蓝色的圆圈，描述了车辆的可能位置。当我们观察到两个地标时，我们就知道机器人或车辆必须位于这两个圆圈的交点，也就是说，我们得到了两个可能的位置，但仍然不能确定机器人的方向。当然，我们可以继续，如果我们可以观察到三个地标，那么我们可以画出三个圆，希望所有的圆都在一个交点相交，然后我们就可以推断出这个单一的交点就是机器人的位置。

consistently identifiable points in the world. E.g. lighthouses, feature points in imaging

一直可以被识别的点，例如灯塔、图像中的特征点

#### what can we conclude from… 2d：我们可以从…中得出什么结论 ?

• the distance to a given landmark?到一个给定地标的距离？
  • robot position on a circle
  • unknown orientatioin
• the distance between two landmarks?到两个给定地标的距离？
  • 2 possible positons
  • unknown orientation
• the distance between three landmarks?到三个给定地标的距离？
  • robot position(some exceptions are possible)机器人位置（可能有一些例外）
  • orientationo unknown

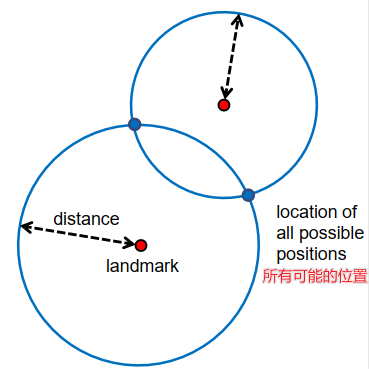
所以，总的来说，如果我们知道距离地标的距离，我们可以确定位置，但我们不能确定方向。那么，如果我们知道我们观察的角度呢？假设我们有一个地标，我们可以确定与我们自我定位的角度，即相对于我们的机器人或车辆自我定位，我们识别到的对象的角度。

答案是，经过一些数学或几何推理后，我们得出的结论是，使用单个地标，我们无法确定机器人的位置，机器人仍然可以位于二维平面上的任何点。但是，如果我们知道机器人的位置，并且我们有一个角度测量，我们可以确定机器人的方向。也就是说，如果机器人位于用蓝圈标出的点，我们在某个角度感知到地标，那么我们可以推断出机器人具有由箭头给出的某个方向。也就是说，知道我们感知到地标的角度允许我们确定机器人的方向，前提是我们知道它的位置。也就是说，对于每个可能的位置，我们得到一个不同的机器人方向。

• the angle, from which a landmark is being observed 地标的角度已经被观测到
  • positon unknown
  • relation between position and orientation

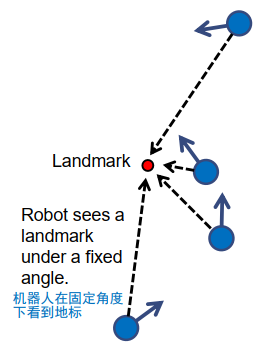
现在，让我们看看如果我们能感知到两个地标，能确定我们观察到这两个地标的角度，会发生什么。 通过一点点的几何知识，我们可以确定，如果我们知道这两个测量值，我们可以创建一个圆弧，我们可以推断机器人必须位于这个圆弧上。这个圆经过两个地标位置，这里用两个红点表示，我们可以推断出机器人必须位于这个圆弧的某个地方。我们还不知道具体是哪个位置，但我们已经可以将它限制在这个圆，这个圆的一部分上。当然，对于每个位置，我们又可以确定机器人的方向。这也意味着，如果我们能够观察到三个地标，并确定我们感知到地标的角度，那么我们可以创建两个或者甚至三个这样的圆弧，它们会在一个交点相交，这意味着，有了三个地标，知道对这些地标的角度，就能确定机器人的位置和机器人的方向。

• the angle from which two landmarks are being observed? 两个地标之间的角度已经被观测到
  • robot position on an arc or line segment 圆弧或线段上的机器人位置
  • relation between position and orientation
  • approch: inscribed angle theorem

linear landmarks 线性地标

我们之前讨论的是，我们可以从地图上的单点地标得出的结论，比如一个灯塔，如果我们将灯塔投影到地面上，它就是一个单点。然而，在实践中，有时候利用环境中的其他对象进行定位是有用的，这些对象并不仅仅是单点。例如，线。我们可以在足球场上找到这些线，足球场上的线，是用于自我定位非常有用的线，它们并不仅仅是单点。或者对于一个自动驾驶的车辆，我们可能想使用车道标记，或者我们可能想使用路缘石，或者某些紧挨着路边的房屋的墙壁，并使用它们作为自我定位的地标。所以问题是，如果我们可以测量到这些地标的正交距离，我们能从这些地标中得出什么结论？

• 例如： roadway lines, curbs, and walls 道路线、路缘和墙壁

what can we conclude from… ：我们可以从…中得出什么结论 ?

• the orthogonal distance,in which a line is being observed 观测一条线的垂直距离
  • position on two parallel lines 两条平行线
  • relation between position and orientation
• the orthogonal distance to two lines 两条线的垂直距离
  • 4 points / 2 points
  • relation between position and orientation

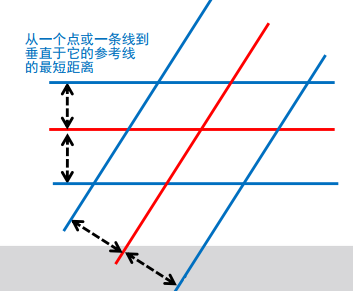
因此，我们假设我们知道某条线或线性地标，我们知道它的位置和它的确切几何形状，我们测量到这个地标的正交距离，想要推断我们在哪里。

好让我们来可视化这个。如果我们假设红线是地标，我们可以测量到一定的距离，由虚线箭头表示，那么我们可以推断出，机器人或车辆必须位于两条与红线平行的蓝线上。也就是说，我们知道，车辆或机器人位于蓝线的其中一条上，我们不知道具体是哪一条，我们也不知道它是位于上面的还是下面的，但我们仍然能够发现，它位于这些线中的一条上。

当然，如果不只有一条线，而是我们可以观察到的两条线，我们可以做一些更复杂的几何推理。对于每条线，我们计算出平行线，它们与地标的距离等于我们感知到的距离，然后必须位于这些平行线上。如果我们考虑下面的图，我们可以推断出，我们最终位于蓝线的四个交点之一。如果两个地标线的交角不是90度，考虑到这些我们构造的线相交的角度，我们甚至可能能够将可能的位置数量限制在两个。

One-Shot Localization 一次性定位算法

“One-Shot Localization” 是指在仅有一次观测或信息的情况下进行定位或位置估计的过程。它是指通过一次观测或一次输入，从未知位置或环境中准确地确定目标的位置或姿态。在传感器技术和机器人领域中，这个术语通常用于描述使用单个数据样本进行位置估计的方法或算法。这种方法可能利用传感器数据、图像处理技术或其他信息源来实现目标的定位。与传统的迭代定位算法相比，One-Shot Localization 着重于通过单次观测尽可能准确地确定目标的位置，从而减少计算和时间成本。

给定：

• a map with a set of landmarks
• a set of boserved landmarks from seen from a vehicle

任务：

• how do I have to shift and rotate the vehicle so that the observed landmarks match best the land marks in the map?
• 我如何移动和旋转车辆，以便观察到的地标与地图中的地标最匹配？

现在，你应该对自我定位如何工作以及基本概念有了基本的了解，所以现在是时候使事情变得更加数学化了。在我们的语境中，地图是一组对象，对于每个对象，我们都知道它的位置。在这个时候，让我们限制到点地标，也就是说，地标可以在地图上仅仅表示为一个单点。在这个例子中，你可以在幻灯片的右侧看到，我们有八个点P1到P8，它们在二维平面上排列。这些向量Pi在固定在世界中的世界坐标系中表示，我用希腊字母I和η表示这个字母坐标系的坐标轴。

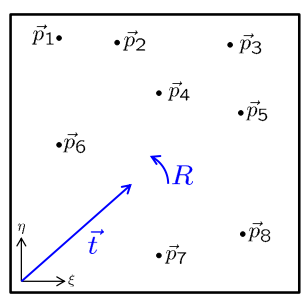
车辆使用其车载传感器进行一些观察，它观察到其中的一些标记。在这个例子中，它可能只观察到2、3、4和5号标记的某些位置，这些位置在车辆坐标系中表示。坐标轴以X和Y表示，所以这并不一定是相机的坐标系，可能是相机的坐标系，但也可能不是。我们可能已经从相机坐标系转换到了一些车辆坐标系，但是这个坐标系本身是随车辆移动的。所以，知道坐标系的原点和坐标系的方向意味着我们也知道车辆的位置和车辆的方向。

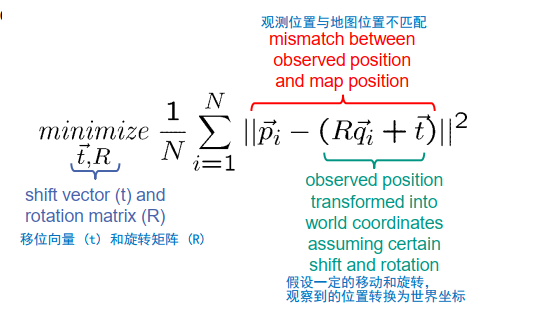
我们的任务是找到一个平移向量和一个旋转矩阵，使得最终我们用车载传感器感知到的位置和地图上的标记位置尽可能的一致。平移向量表示车辆的位置，旋转矩阵表示车辆的方向。所以，任务是找到这个平移向量和这个旋转矩阵。我们如何做到这一点呢?

为此，我们需要一些数学。因为最终我们想解决一个优化问题。所以我们首先陈述优化问题，然后讨论如何解决它。

我们再次开始从地图上的点位置，它们由向量Pi表示，所以P1指的是第一个标记，P2指的是第二个标记，以此类推。车载传感器检测到的观察标记位置在车辆坐标系中表示，并由qi表示。我们假设索引与标记的索引一致，也就是说，qi指的是位于位置pi的标记。如果不是这样，我们只需要重新编号所有的标记就可以得到这个结果，这只是一个简化表示的技巧。现在，我们想要解决以下的优化问题，以确定车辆未知的位置和方向。

让我们看看这个术语的细节。在这个部分，我们计算r乘以qi加t，这是什么呢？Qi是从车载传感器看到的第i个标记的感知位置。如果R和T是车辆的真实方向和位置，那么R乘以qi加T就是将观察到的第i个标记投影到世界坐标系中。

这也意味着，pi减去rqi加T是真实位置的第i个标记pi和投影位置的标记rqi加T之间的差值。当然，我们期望这两个位置非常接近，这意味着这两个向量之间的差应该是一个非常短的向量。因此，我们计算该向量的长度，即欧几里得长度，并取其平方。这个表达式应该是小的，而且它不仅应该对单个标记小，而且应该对我们观察到的所有标记都小。因此，我们将这些项加总。

最后，我们希望找到最小化这个误差项的T和R的值，并认为这些最小化误差项的T和R的值是车辆最可能的位置和最可能的方向。

数学方法：mathematically

• which movement (translation + rotation) transforms vehicle coordinates into world coordinates such that observed landmark positions fit to map position?
• 哪种运动（平移+旋转）将车辆坐标转换为世界坐标，以便观察到的地标位置适配到地图位置？

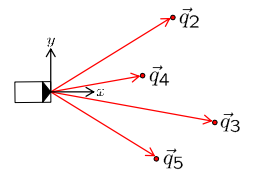
• landmark positions in world coordinates (map) 世界坐标中的地标位置（地图）：

• observed landmark positions in vehicle coordinates 在车辆坐标中观察到的地标位置:

现在，我们已经看到了优化问题，但是如何解决这个优化问题还不清楚。

我们想要最小化这个依赖于未知旋转矩阵和平移向量的误差项。为了简化接下来的步骤，我们首先做一些替换。我们引入P bar作为我们观察到的所有标记的平均位置，所以它是1除以n乘以所有标记位置的和，即所有这些标记的重心。我们引入新变量p i Prime，它等于Pi减去P bar，这意味着我们从所有的标记中减去了重心，然后对于这些p i Prime变量，我们知道它们的平均值最后是零。我们对qi变量做同样的操作，我们引入Q Bar作为qi变量的重心，并从每一个qi测量中减去这个重心，得到qi Prime值。现在，我们在误差项中将Pi替换为Pi prime加P bar，将Q I替换为q i prime加Q Bar，得到最底部的项。

• optimization problem:

所以现在我们看到了优化问题，但是还不清楚我们如何解决这个优化问题。

现在我们可以更详细地看看不同的部分。我们可以看到，在这一点上，我们有所有的p i Prime变量的平均值，但我们选择了这样的pi primes，使得它们的平均值等于零，所以这个项实际上等于零。同样的，对于QI Prime部分也是如此，我们选择了QI Prime变量，使得它们的平均值等于零，所以我们得到了零向量，零向量乘以旋转矩阵R也会得到零向量，所以整个和的右边的括号内的项总和等于零，这意味着我们可以忽略掉整个和的第三部分，将项简化为我们在第五行找到的那样。现在我们可以看看第二项，它是P bar减去r乘以Q Bar减去t的平方范数。你可以观察到，第一项不依赖于平移向量T，只依赖于旋转矩阵R，只有第二项依赖于平移向量。这意味着，无论我们找到的旋转矩阵是什么，我们总是可以确定一个适当的平移向量T，使得第二部分等于零，即通过选择t等于P bar减去r乘以Q Bar。对于这样的向量T的选择，第二项总是等于0，并且取得最小值。所以，我们已经知道如何根据R来选择T，剩下的就是第一项。现在的问题是，我们如何确定旋转矩阵R，使得第一项最小。这个第一项可以再次被重写。所以，再次我们看到，我们有这个欧几里得距离的平方，欧几里得距离中有两个变量的差，我们可以再次分解这个平方欧几里得距离，得到我们在这里看到的结果。所以，实际上这是两个项的和，第一项是p i Prime的长度的平方，我们将它视为常数，并将它提出来。然后我们有QI Prime，QI Prime变量在旋转矩阵R的作用下，再加上p i Prime和r乘以QI Prime的标量积的两倍。这意味着，我们可以找到一个矩阵R，使得所有的pi Prime的向量和所有的r乘以QI Prime的向量成正比，那么第一项会消失，我们得到的只是这个求和，它是关于所有的标记的，它包含了所有标记位置的平方长度的和，这是一个常数。所以我们得到的就是一个常数减去另一个项，而这个项实际上是这个对应的标量积的两倍。

• 最小化下面的式子：minimize

with：

最大化：

$\sum_{i=1}^N\left(\vec{p}_i^{\prime}\right)^T R \vec{q}_i^{\prime}$

所以现在的问题就转化为找到一个旋转矩阵R，使得所有的PI Prime和所有的R乘以QI Prime的向量尽可能的接近。这个问题可以通过奇异值分解来解决。我们可以定义一个新的矩阵S，这个矩阵是对应于每个观察到的标记，每个观察到的标记都产生一个对应的项，这个项是qi Prime乘以pi Prime的转置，这样我们得到一个3乘3的矩阵，我们将这些矩阵加起来，就得到了我们的矩阵S。然后我们对这个矩阵进行奇异值分解，得到U，D和V，然后我们可以得到旋转矩阵R，即UV的转置。

总结一下，我们找到了一个能够最小化我们的误差项的旋转矩阵R和一个平移向量T。对于T，我们只是选择了让我们误差项中的第二部分最小化的向量。然后，我们通过奇异值分解来寻找最优的旋转矩阵R。

这就是我们如何进行点云配准，或者说，如何找到最适合我们观察到的标记的车辆的位置和方向。

我们现在需要最大化这个项，包括因子R，这有点复杂，有几种方法可以做到这一点。我在这里介绍的方法基于一个叫做奇异值分解（SVD）的技术。为了应用它，我们需要以以下方式稍微变换这个项。经过一点点尝试，你会发现p_i‘转置乘以R再乘以q_i‘转置的和可以被重写为R矩阵的迹乘以q_i‘乘以p_i‘转置的和，简单来说，就是矩阵R和H的迹，其中H是对q_i‘和p_i‘转置向量的求和。

因为q_i‘和p_i‘是列向量，所以H是一个2x2的矩阵，如果我们处理的是二维位置的p_i‘和q_i‘，或者它是一个3x3的矩阵，如果我们处理的是三维向量的p_i‘和q_i‘。这个关系可能不易看出，但你可以试试看并轻松证明出来，如果你不信任的话，就试试看。所以，矩阵的迹是什么呢？矩阵的迹就是矩阵对角线元素的和。

现在让我们看看奇异值分解。奇异值分解是线性代数中的一个定理，它声明对于任何实矩阵H都存在正交矩阵U和V以及对角线上有非负项的对角矩阵D，使得H等于UDV转置。所以我们可以把任何实值矩阵H分解为两个正交矩阵、一个对角线上有非负项的对角矩阵和另一个正交矩阵的乘积。

注意，矩阵U和V是正方形矩阵，而矩阵D可能是一个非正方形的长方形矩阵。根据H的大小，在我们的例子中，H本身就是一个正方形矩阵，因此U、V和D都是正方形矩阵。

我们并不想证明这个定理，你可以在所有线性代数的教科书中找到它，它对于数值计算非常重要，但在这里我们只是想使用这个结果。

经过一些推理，我们可能会发现我们可以将我们上面显示的优化问题解决为以下解决方案：如果H分解为UDV，使用奇异值分解，那么我们期望的旋转矩阵，它最大化这个误差项，就计算为V乘以U转置，如果V乘以U转置的行列式等于1，或者它是V乘以对角线上除最后一项外其他项都是1的对角矩阵，最后一项是-1，再乘以U转置。所以如果V乘以U转置的行列式等于-1，那么这个情况就是有效的。这就是解决方案。

所以我们基于q_i‘和p_i‘的值计算H，然后我们用奇异值分解计算U和V，然后我们检查V和U的行列式，并检查V和U的行列式是否等于1，然后我们返回V乘以U转置，或者V乘以对角线上的元素都是1，除了最后一个元素等于-1的对角矩阵，再乘以U转置。如果你想检查证明，你可以查看原始论文，它显示在底部的行中，这个证明不是很复杂，我认为你有机会理解它，它并不太难，但它需要一点点技术思考和一点点数学。

所以现在我们知道我们怎么计算那些最优的旋转矩阵R和平移向量T，然而我们假设我们确切地知道我们正在观察哪些地标，也就是说，我们能够准确地识别每一个地标。这在某些情况下可能是不可能的，例如，假设我们正在处理特征点方法，并且我们使用车辆环境中的特征点作为地标。每个特征点都带有一个描述符，这些描述符或多或少都是独一无二的，所以一旦我们确定了这样一个特征点，我们就知道我们观察到了哪个特征点，不仅仅是在某个位置有一个特征点，而且我们确切地知道我们观察到了哪个特征点，所以我们知道我们要考虑哪个p_i变量。这并不总是这样，例如，如果你假设我们正在处理道路上的交通标志，我们观察到了某个交通标志，我们想把它作为一个地标。当然我们可以分析这个交通标志，我们可以区分不同的交通标志，所以我们不会把停止标志和优先道路标志混淆，例如，但是还可能有几个停止标志或者几个交通标志有完全相同的外观，那么我们就不能说我们观察到了地标5号或者地标10号，但我们只能说，好吧，我们观察到了一些地标，但我们并不确切地知道我们观察到了哪些地标。这当然是更复杂的情况，其中地标并不能被唯一识别。我们如何扩展这种方法，以处理这种情况？

• 不同的方法，例如 SVD：

• mathematical theorem (singular value decomposition, SVD): for every real matrix H exist orthogonal matrices U,V, and a diagonal matrix D with nonnegative entries, such that: 数学定理（奇异值分解，SVD）：对于每个实数矩阵 H，存在正交矩阵 U、V 和具有非负项的对角矩阵 D，使得：$H=U D V^{T}$

• solution：

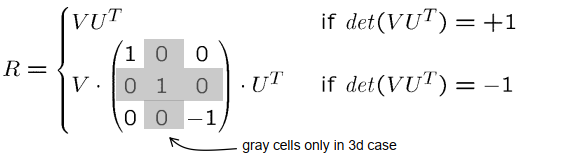
• what to do if landmarks are not uniquely identifiable?如果地标不是唯一可识别的怎么办？
  • $\vec{q_{i}}\ \mathrm{\bf~might~rester~to~any~of}\ \ \vec{p_{1}},\ …,\vec{p_{i}},…$
• brute force solution: try all possible combinations 蛮力解决方案：尝试所有可能的组合
  • computationally too expensive 计算成本太高

当然，总会有一个暴力解决方案，我们可以尝试所有可能的组合，这就意味着我们假设我们观察到了地标1，我们假设我们观察到了地标2，我们假设我们观察到了地标3，等等，所以我们可以枚举所有可能的组合，并对每一个都计算剩下的误差，然后在所有这些组合中搜索最小值。然而，这在计算上似乎比较昂贵，因为可能的组合的数量增长非常快，通常我们不仅仅处理5个或10个不同的地标，而是处理几百个或几千个地标，这些地标的组合数量如此之大，以至于我们在实时计算中永远无法解决这个任务，所以我们需要找到另一种解决方案。我们的想法是使用迭代的贪婪分配策略，我们假设我们知道一个整数，我们有车辆位置和车辆方向的初始猜测，基于此，我们可以将所有观察到的地标投影到地图上，然后我们可以在地图上搜索最近的地标，也就是说，对于每个q_i，我们搜索地图上最近的地标，考虑到车辆位置和车辆姿态的初始猜测，然后我们使用这些地标作为分配的真地标，并应用我们刚刚介绍的算法来计算最优的旋转和平移。当然，在计算了这个旋转和平移之后，我们可能会发现，现在投影所有观察到的地标会得到另一个分配，也就是说，在计算了这个旋转和平移，得到了车辆位置更好的猜测之后，我们可能会发现，现在一个特定的观察到的地标更接近另一个地标，而不是我们在前一步中假设的那个地标。所以在这种情况下，我们需要重新分配所有的观察，然后再计算R和T的最优参数。这提供了一个更好的车辆姿态的猜测，再次，我们将所有观察到的地标投影到地图上，到世界坐标系中，并比较哪个地标在地图上是最近的。根据这个，我们分配观察到的地标和地图上的地标，我们再计算一个旋转矩阵和平移向量，这提供了一个更好的车辆姿态的猜测，等等，直到整个过程收敛。这产生了一个被称为迭代最近点的算法，或者ICP算法。

• iterative, greedy assignments: 迭代，贪婪的分配：
  • $\text { assign } \vec{q}_i \text { to closest landmark among } \vec{p}_1, \ldots, \vec{p}_i, \ldots$
  • reassign all observations incrementally 逐步重新分配所有观察结果
  • 👉 ICP algorithm 迭代最近算法

ICP algorithm 三维点云配准

ICP（Iterative Closest Point）算法是一种迭代的点云配准算法，用于将两个或多个点云之间进行对齐和匹配。它是一种常用的三维点云配准算法，在计算机视觉、机器人和地图构建等领域得到广泛应用。

ICP算法的基本思想是通过迭代的方式，将待配准的目标点云与参考点云对齐，使它们在空间中尽可能重合。算法的核心是找到两个点云之间的最佳刚性变换（旋转和平移），使得它们的重叠部分最大化。

如果我们在步骤四中的分配方式与上一轮循环中的不同，那么我们需要继续进行步骤八。如果相同，意味着在上一轮我们将观察值分配给了相同的地标，那么我们知道算法已经收敛，不会再有任何改变，此时我们可以退出循环，并返回计算得出的旋转矩阵和平移向量。如果不是这种情况，我们就执行步骤八。在步骤八中，我们应用幻灯片10到12中介绍的算法，计算尽可能最好地将点从Q映射到P的新变换R~和t~。

然后，我们把到目前为止计算得出的变换进行串联。我们的前一个猜测是车辆的位置T和车辆的方向R，通过这个增量步骤，我们用矩阵R~和t~进行确定。串联这些变换后，我们得到一个新的旋转矩阵R为R~ * R，新的平移向量或车辆位置t为R~ * t + t~。这样我们就可以一直进行循环，直到我们能在步骤六中退出循环。

如前所述，这种算法被称为迭代最近点，简称ICP算法，于1992年提出。它可以用来找到车辆的最优位置和最优方向，如果我们观察到一组点地标，并且我们不能确定我们究竟观察到了哪些地标。算法保证会在某一点终止，它会收敛到这个误差项的局部最优解，不一定会收敛到全局最小值，这非常依赖于车辆姿态的初始猜测。如果初始猜测是好的，ICP算法很可能会收敛到全局最小值。如果初始猜测是差的，它可能不会收敛到全局最小值，只会收敛到次优的局部最小值。

如果我们遍历这个算法，我们会看到在算法的每一步中，这个误差项都在减少或保持不变。这尤其适用于我们重新计算R和T的步骤八，因为在这里我们直接解决了一个优化问题，并且我们已经看到我们找到了这个优化问题的解析解。这意味着我们可以得出结论，我们真正达到了最优解，全局最优解，假设在pi和Qi地标之间的分配是固定的。

此外，在我们重新分配qi点到pi点中最近的点的步骤四中，我们也减少了这个误差项的值，或者我们保持它不变，但我们从不增加这个距离项e。这意味着在整个循环中，在这个循环中的所有步骤中，我们都在减少这个误差项，或者我们保持它不变，所以它永远不会增加，这是一个重要的属性。此外，我们知道，qi点和pi点之间的可能分配数量是有限的，可能很大，但仍然是有限的。如果我们有这样一个有限数量的可能性，并且我们有一个在这些可能性之间的序列，使得误差项总是变小或保持不变，那么我们可以得出结论，从某一点开始，我们总是有这样的配置，在这种配置中，误差已经达到了最小，而且不再减小。这种观察到一个单调递减序列的有限集合的可能性的原则，被称为鸽巢原理或德里克雷原理。从这个论点我们可以得出结论，从某一点开始，算法收敛，这意味着这些分配不再改变，算法终止。

• Iterative Closest Point (ICP)(Besl, McKay 1992)
  • calculates rotation $R$ and translation $\overrightarrow{t}$ in order to transform a set of points $Q$ onto another set of points $P$ 计算旋转矩阵 $R$ 和平移向量 $\overrightarrow{t}$，以将点集 $Q$ 变换到另一个点集 $P$
  • ICP always terminates ICP总是终止
  • ICP converges to local minimum of
    收敛到局部最小值

• 简要证明
  • by construction, $E(R,\overrightarrow{t})$ is minimized in step 8 assuming fixed assignments between points 根据结构，在步骤8中，$E(R,\overrightarrow{t})$是最小化的，假设点之间有固定的分配。
  • by construction, $E(R,\overrightarrow{t})$ is minimized in step 4 assuming fixed translation and rotation 根据结构，在步骤4中，假设固定的平移和旋转，$E(R,\overrightarrow{t})$被最小化了
  • hence, $E(R,\overrightarrow{t})$ never increases
  • since number of possible assignments is finite, we cannot generate new permutations in step 4 from a certain point on (pigeonhole/Dirichlet principle) 由于可能的分配数量是有限的，我们不能在第 4 步中从某个点生成新的排列（pigeonhole/Dirichlet principle）

ICP example 1

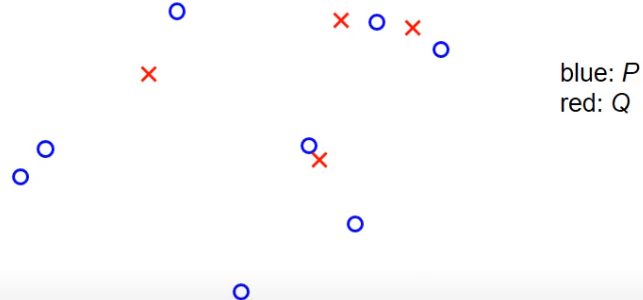
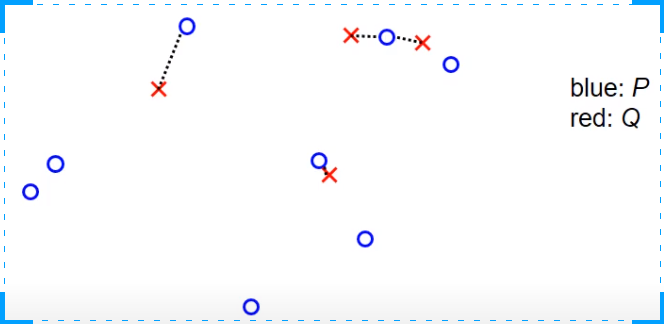
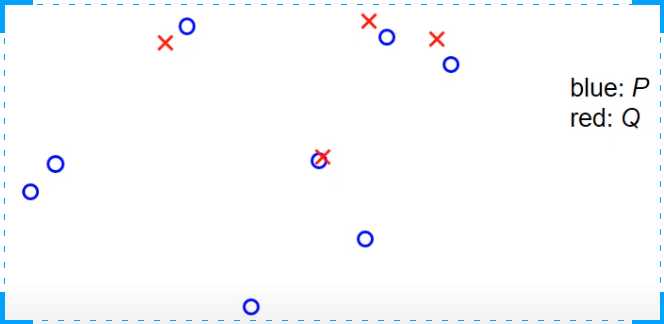
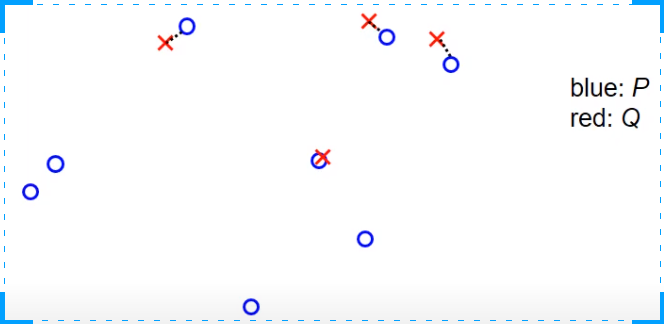
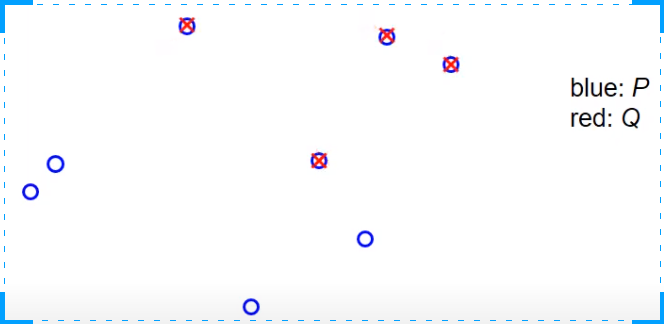
ICP算法的一个例子是，有一个非常小的观察集。在这里，蓝色的是集合P，也就是地标在世界坐标系统中的真实位置，红色的是观察值，它们是使用车辆位置的某个初始猜测投射到世界坐标系统中的。任务是以某种方式旋转和平移红色的交叉点，使它们与蓝色的圆圈更或少的重合。在第一步中，我们搜索最近的点，对于每个红色的交叉点，我们搜索最近的蓝色圆圈，这是由虚线表示的。如我们所见，可能会出现两个观察值，对于两个红色的交叉点，分配给同一个地图中的地标的情况，这并不是算法的问题，我们不关心这个，我们就把它当作它是的。下一步是我们计算一个旋转矩阵和一个平移向量，以某种方式推动交叉点和圆圈一起。在这之后，我们再次投射红色的交叉点，也就是观察到的测量值到世界坐标系统中，现在的情况可能看起来像这样。再次，我们检查在P中最近的点，也就是在这种情况下最近的蓝色圆圈，并将红色交叉点分配给蓝色圆圈。然后我们再次计算旋转矩阵和平移向量。应用它们会使红色交叉点完美地移动到蓝色圆圈中。现在，如果我们再次搜索每个红色交叉点的最近点，我们会发现红色交叉点和蓝色圆圈之间的分配保持不变，所以算法必须停止，我们可以返回结果旋转和平移。

ICP example 2

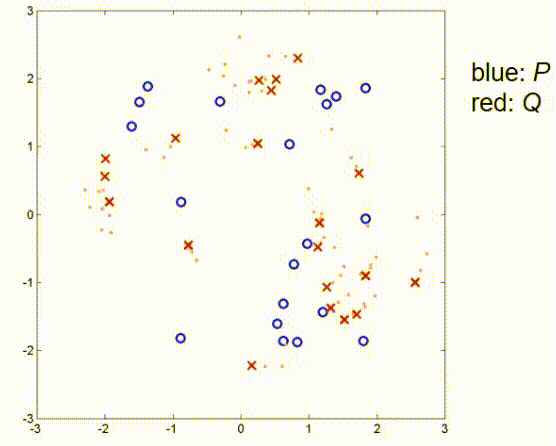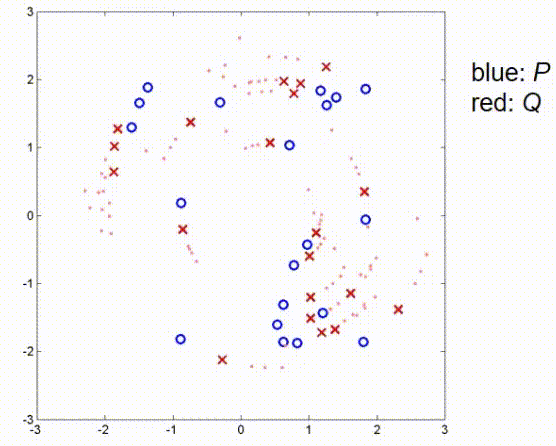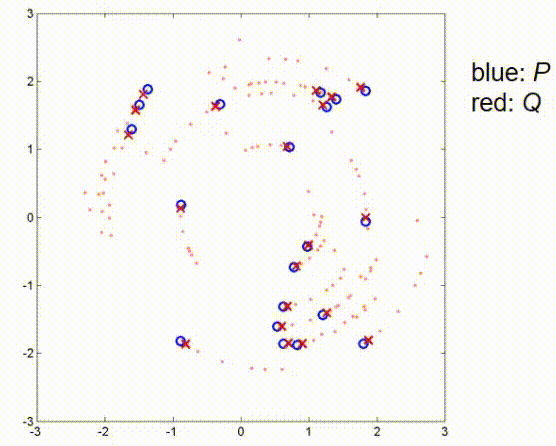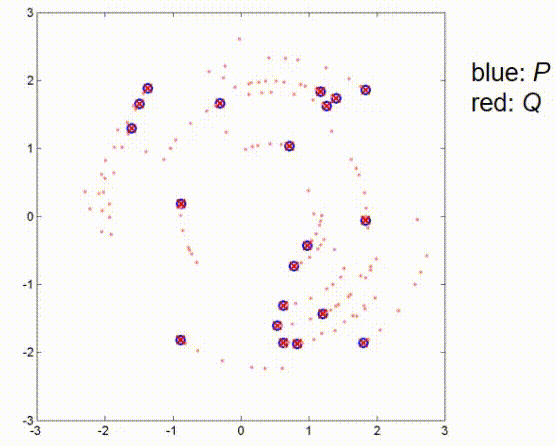
这里有另一个例子，包含一些更多的点。这个例子包含一些随机采样的蓝色点，观察值是通过将蓝色点旋转45度并添加一些小的偏移量创建的。我没有添加任何噪声，所以我们假设有一个完美的传感器，没有任何不精确。那么，如果我们应用ICP算法，算法会进行几个步骤。

现在，它已经收敛。如我们所见，在这些条件下，算法仍然能够找到全局最优。接下来我们看一个观测测量值和真实位置之间有较大平移的例子，这里我们有一个大的偏移，没有噪声。在这里，ICP算法的第一步是将红点向蓝点推动，使得它们的重心重合，然后再次补偿45度旋转，直到算法收敛。

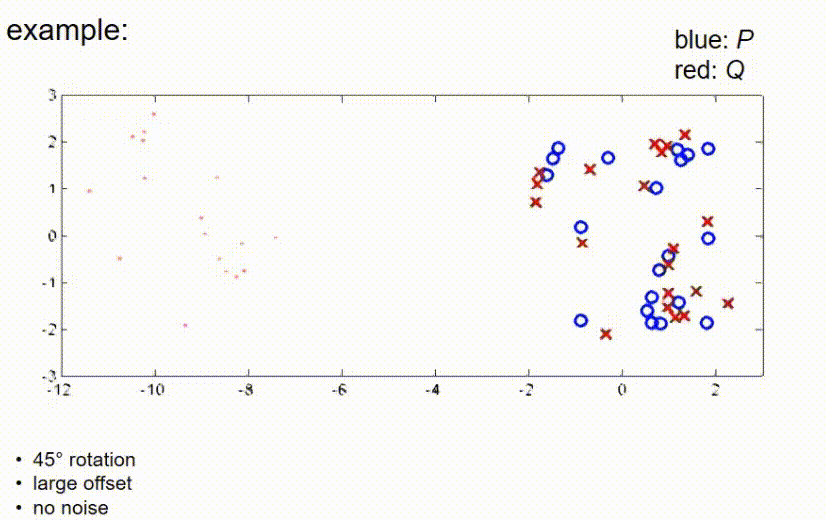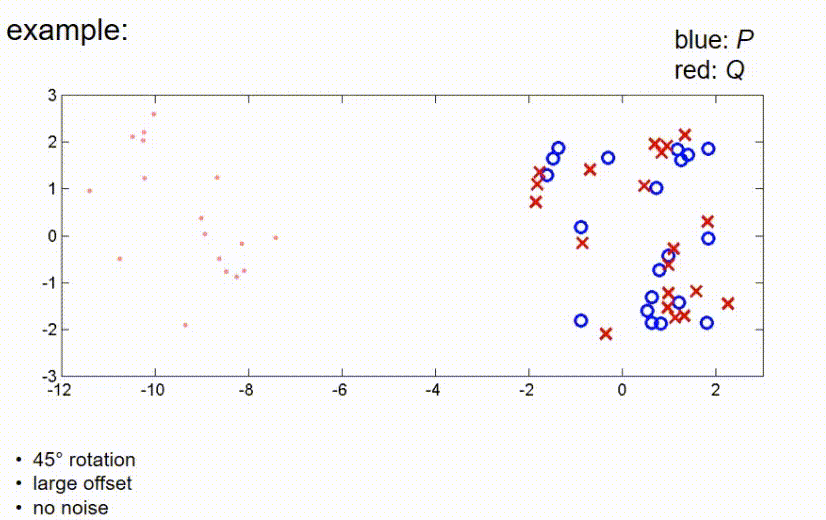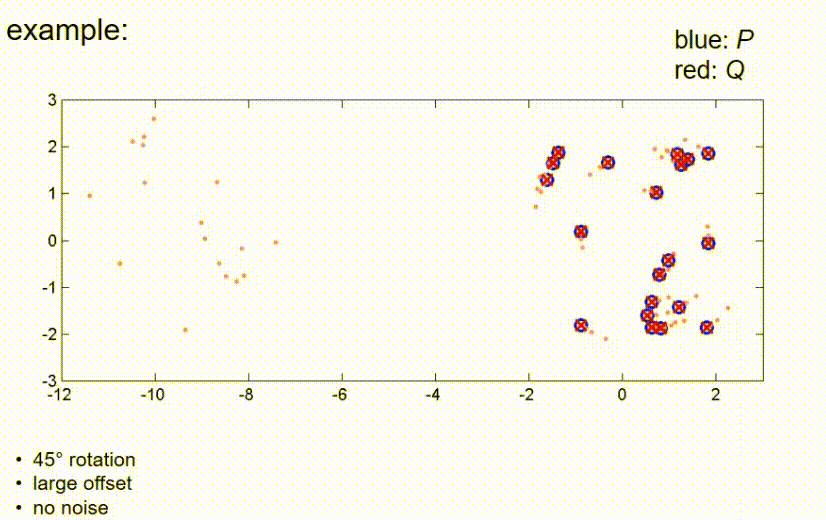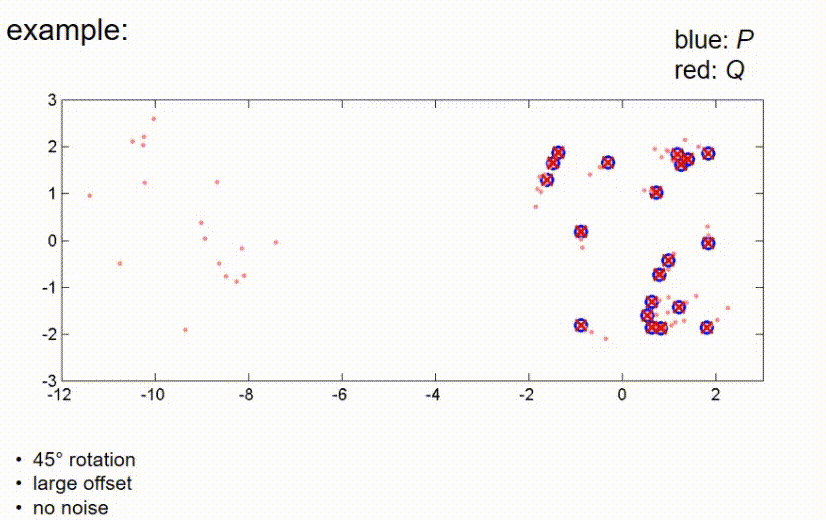
ICP example 3

接下来我们看一个观测测量值和真实位置之间有较大平移的例子，这里我们有一个大的偏移，没有噪声。在这里，ICP算法的第一步是将红点向蓝点推动，使得它们的重心重合，然后再次补偿45度旋转，直到算法收敛。

ICP example 4

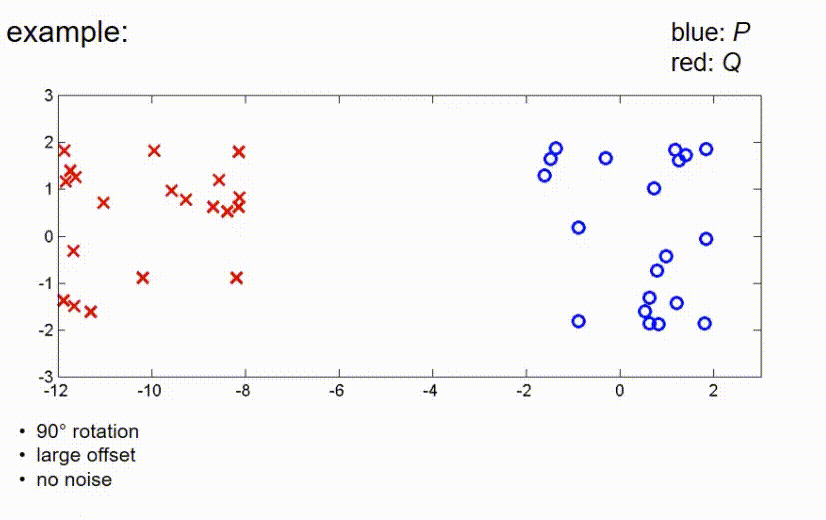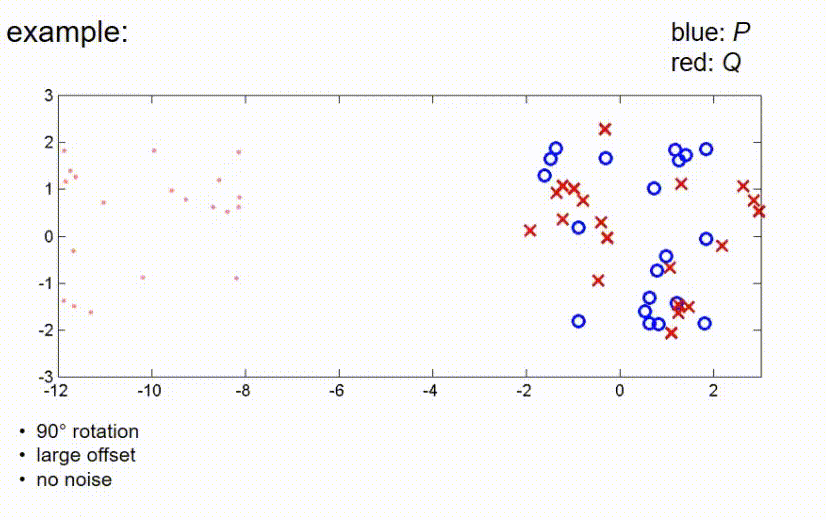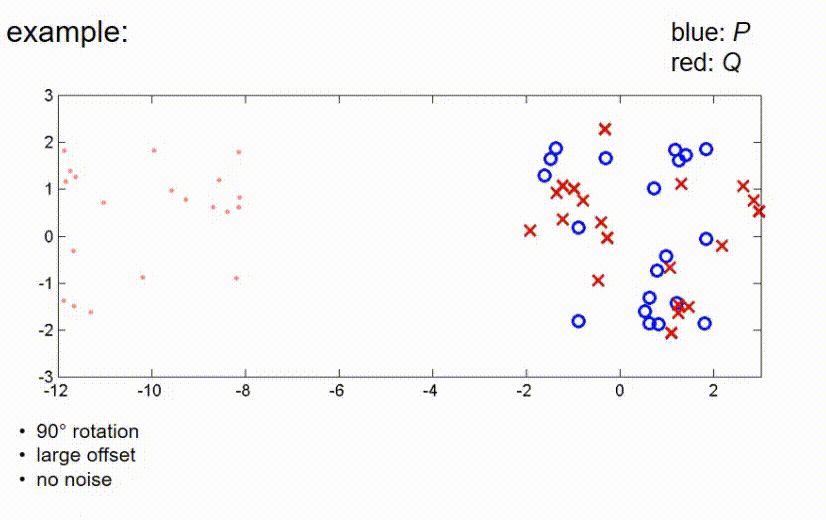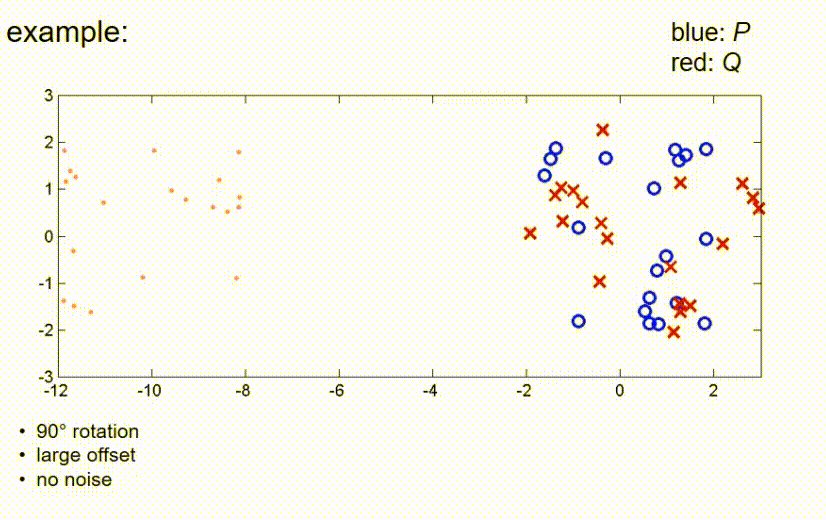
再来一个例子，偏移很大，但现在旋转90度。我们开始算法的第一步，算法使得重心重合，然后稍微旋转一下红点，但只是这样。现在，算法已经收敛，我们可以看到它收敛到一个局部最小值，而不是全局最优。

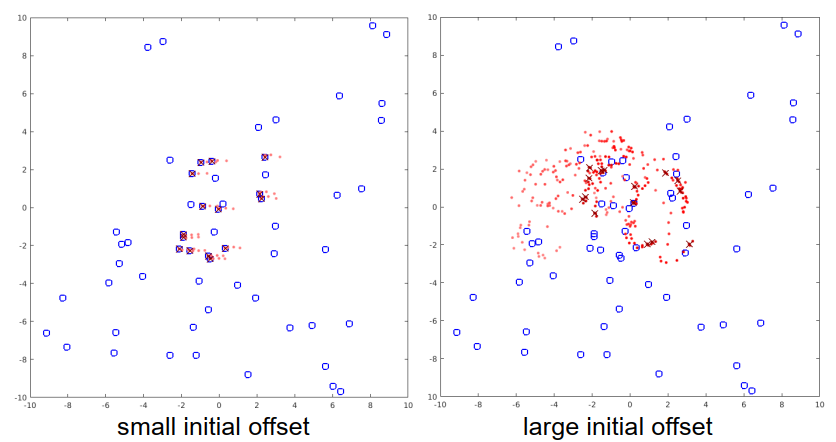
这个展示了一个情况，即地图中的地标数量（也就是集合P）比观测到的地标数量（也就是集合Q）要多得多。这在应用中是很典型的，因为我们假设地图包含了大面积的区域，所以它有来自这个大面积的所有部分的地标。然而，机器人或者车辆只能观测到它的局部环境中的地标，它不能观测到所有其他的地标。所以，观测到的地标只会是地图中所有地标的一个子集。当我们看到找到的位置时，我们可以看到，在左边，只要ICP开始时假设的位置和真实位置之间的偏移足够小，ICP算法仍然适用于这种场景。然而，如果这个偏移过大，我们可以在右边看到，我们虽然收敛，但我们没有收敛到全局最优或真实位置，而是收敛到一个远离全局最优的局部最优。这是ICP的典型行为，只有当我们有足够好的姿态的初始猜测时，它才会收敛。

ICP example real

让我们看一个真实的例子，即机器人足球。正如我们在开始时介绍的，我们可以使用场地标记作为地标，并使用机器人上的摄像头来检测摄像头图像中的这些线，然后我们可以以某种方式使用ICP算法或者ICP算法的变体来计算观测线和地图中线的最佳匹配。

在这里，我们的想法是使用这种足球机器人中使用的全向摄像头的摄像头图像，这些摄像头可以感知到机器人的整个环境，你可以在中心的摄像头图像中看到这一点。我们看到的是摄像头的镜头，它在摄像头顶部反射在一个镜子上。所以这就是所谓的中心，然后我们看到的一些部分是这个镜子在摄像头顶部的安装。这些区域当然不是我们感兴趣的，我们对那些不感兴趣的区域进行了遮罩，所以这里用灰色的像素遮住了这些区域。这些区域不是我们算法要考虑的。现在我们在图像中搜索场地标记，为了在此过程中保持高效并不浪费太多时间，我们做的是我们在一些搜索线或者搜索光线上进行搜索，这里用红线表示。我们只考虑这些线上的像素，我们遵循这些线，每当我们发现一些白色像素，它们被绿色像素跟随，我们就说这里必须有一个场地标记的元素。所以这会产生一些点，这些点可能是我们用这种摄像头能检测到的。我们可以识别到距离3.5米的场地标记。当然这项工作有点旧，这是在2003年到2008年之间完成的工作。所以现在，使用新的高分辨率摄像头和更强大的计算机，这个算法当然也适用于更远的场地标记。现在我们将所有检测到的场地标记转换到车辆坐标系中，也就是固定在机器人中心的坐标系，其x轴指向前方，y轴指向左边，或者反过来，这种情况下，x轴指向右边，y轴指向前方。这在这个图中产生了黑色的菱形。现在我们知道有一个足球场的地图，也就是我们知道场地标记在哪里，我们使用了ICP算法的一种数值变体来通过最小化观测点与真实场地标记位置之间的距离来确定机器人的位置和方向。最后，在优化后，我们可能已经确定了机器人位于它的目标前方，稍微向左旋转，就像你在图中看到的那样。这种方法对于足球角色扮演工作得非常好。

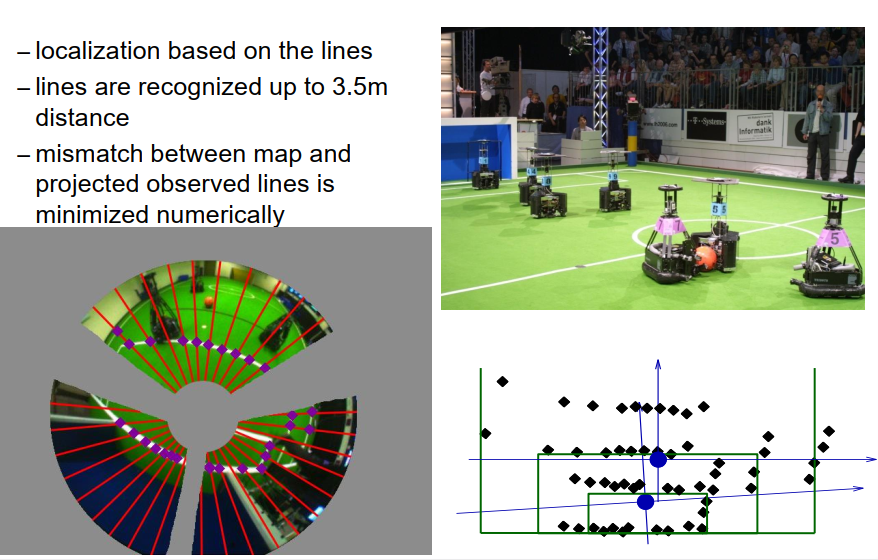
在这里你可以看到一个例子，右边我们再次看到了足球场，在蓝色中我们看到了观测到的场地标记，在计算出最佳匹配后。

在这种情况下，我们得到了优化问题的唯一解，或者更准确地说，因为足球场是对称的，我们得到了两个解，一个我们可以在这里看到，另一个就在场地的对方。然而，除了这种歧义性，我们得到了一个唯一的解。在左侧，我们看到我们实际上最小化的误差项。误差项用灰度值表示，像素越深，误差越大。当然，除了场地标记像素的线外，这些线在这里仅仅是为了比较的目的。我们可以看到，最优解（蓝圈的中心）确实是误差项的全局最小值。我们也可以看到，这个误差项是高度复杂的，因此存在许多局部最小值。

这是另一个例子。

再次，对于我们在误差项图中看到的每个位置，我们可以看到剩余的误差，那是对于该像素位置的最佳方向的误差。我们可以看到，在这种情况下，只找到了一条线上的元素，这导致了一个问题，因为如果你只看到一条线，我们不能确定机器人的完全位置，我们只能说机器人位于两条平行线中的一条上，但我们不知道机器人位于线的哪个地方。就像我们在误差图中看到的那样，有两个小误差项的值是平行于我们看到的线的。在这种情况下，我们可以确定关于机器人位置和机器人方向的一些信息，但不是全部信息。

Incremental Localization 增量本地化

我们如何克服在自我定位中找不到唯一解的情况呢？一种方法是使用增量式定位。通常，我们不是在没有任何关于我们可能在哪里的先验知识的情况下被问到”你在哪里”，而通常是你想知道车辆在哪里，并且我们已经知道机器人在一段时间前的位置。所以我们可以使用这个先验知识来确定现在的位置，这实际上就是增量定位。

这结合了两种技术，一种是我们介绍过的一次性定位，例如使用ICP算法，它在没有任何先验知识的情况下取一些地标，并确定机器人的位置；另一种是追踪方法，如卡尔曼滤波器或回归，它假设我们已经对当前状态有了一些了解，对于这个自我组织问题来说，就是车辆当前的位置，并用我们通过车载传感器获取的当前测量来更新它。这种增量定位的优势是，它比一次性定位更稳定，比一次性定位更高效，它可能为误差项最小化创造适当的图像值，例如对于ICP算法，我们可以做一个初步的相关地标选择，所有类型的数据关联或门控技术。我们还可以容忍有少量地标的区域，所以如果我们看到的地标太少，我们仍然可以依赖我们之前的位置和我们是如何移动的来确定我们现在的位置。

基本的思路很简单，我们假设我们使用一种状态空间模型，其中车辆的姿态（即车辆的位置和方向）产生一个状态空间。我们有一个过滤后的姿态，这是我们现在所在位置的先验知识。然后我们可以应用一个预测步骤，例如卡尔曼滤波器，以得到一个预测的姿态。然后我们使用车载传感器进行测量，并使用一些类似ICP的算法确定这些传感器的姿态。然后，我们使用这个姿态来刷新我们对车辆姿态的了解，这样我们就可以再次获得过滤后的姿态。这个步骤很简单也很容易。当然，我们需要一个初始猜测，无论是预测的姿态还是过滤后的姿态，以完成整个过程。

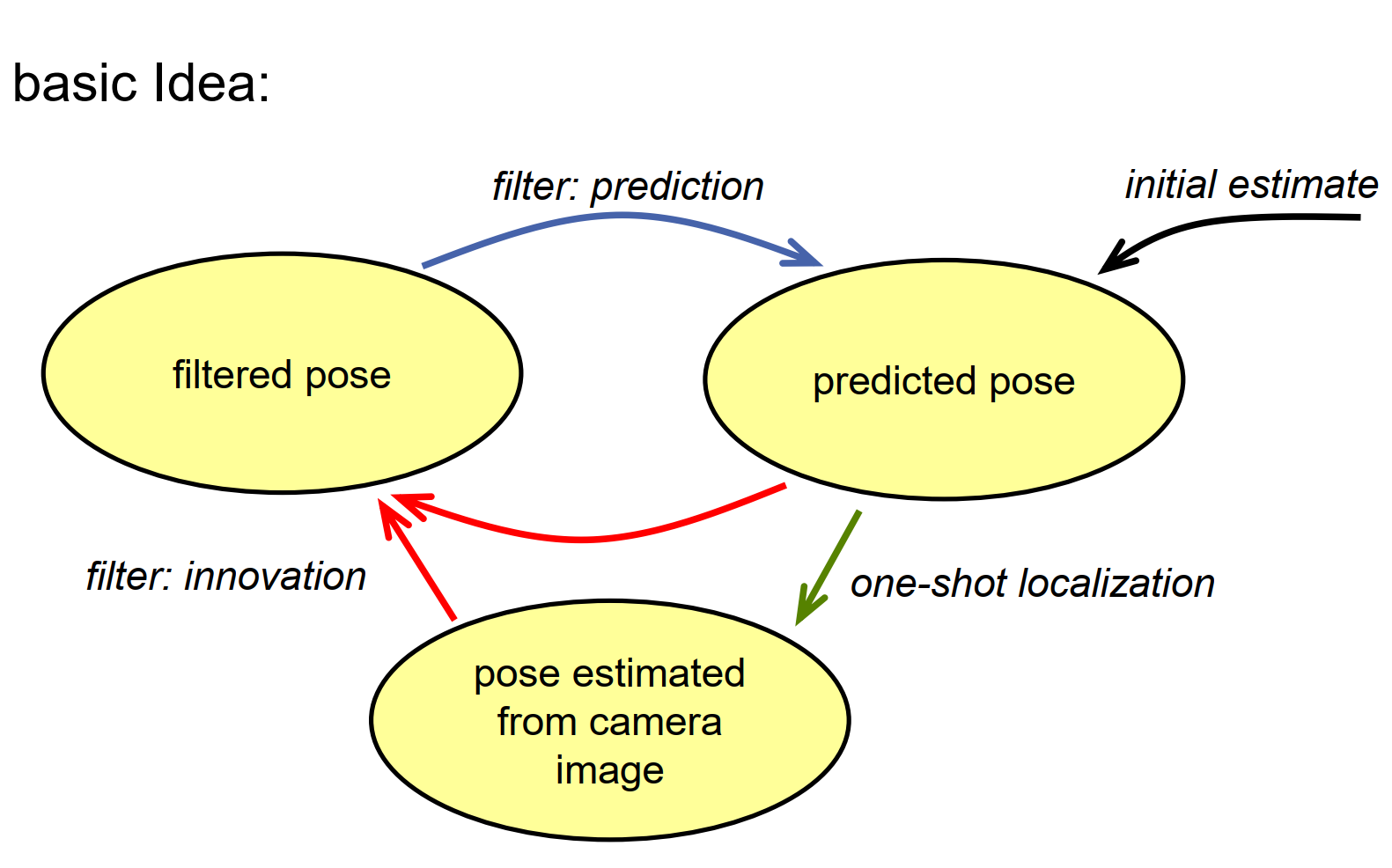
让我们看一个机器人足球定位的例子。我们从一个过滤后的姿态开始，这反映了我们之前所在位置的先验知识，如在小型足球场地图中显示的红色十字标志。然后，我们可能使用卡尔曼滤波器来预测过滤后的姿态，并得到预测的姿态，如这里显示的蓝色十字标志。我们也可能使用机器人的里程计，也就是测量轮子转动的程度，例如轮子的旋转程度，来确定我们已经开多远了，是在转弯还是在直线行驶。现在，我们有了预测的姿态，从那里开始，我们开始最小化误差项的过程，预测的姿态作为初始猜测，所以它可以提高搜索算法的效率。搜索算法收敛到误差项的局部最小值，得到一个从摄像机图像中确定的最佳位置，然后我们使用它作为卡尔曼滤波器创新步骤的测量值。所以现在我们已经闭环了，我们可以像这样以增量的方式继续下去。

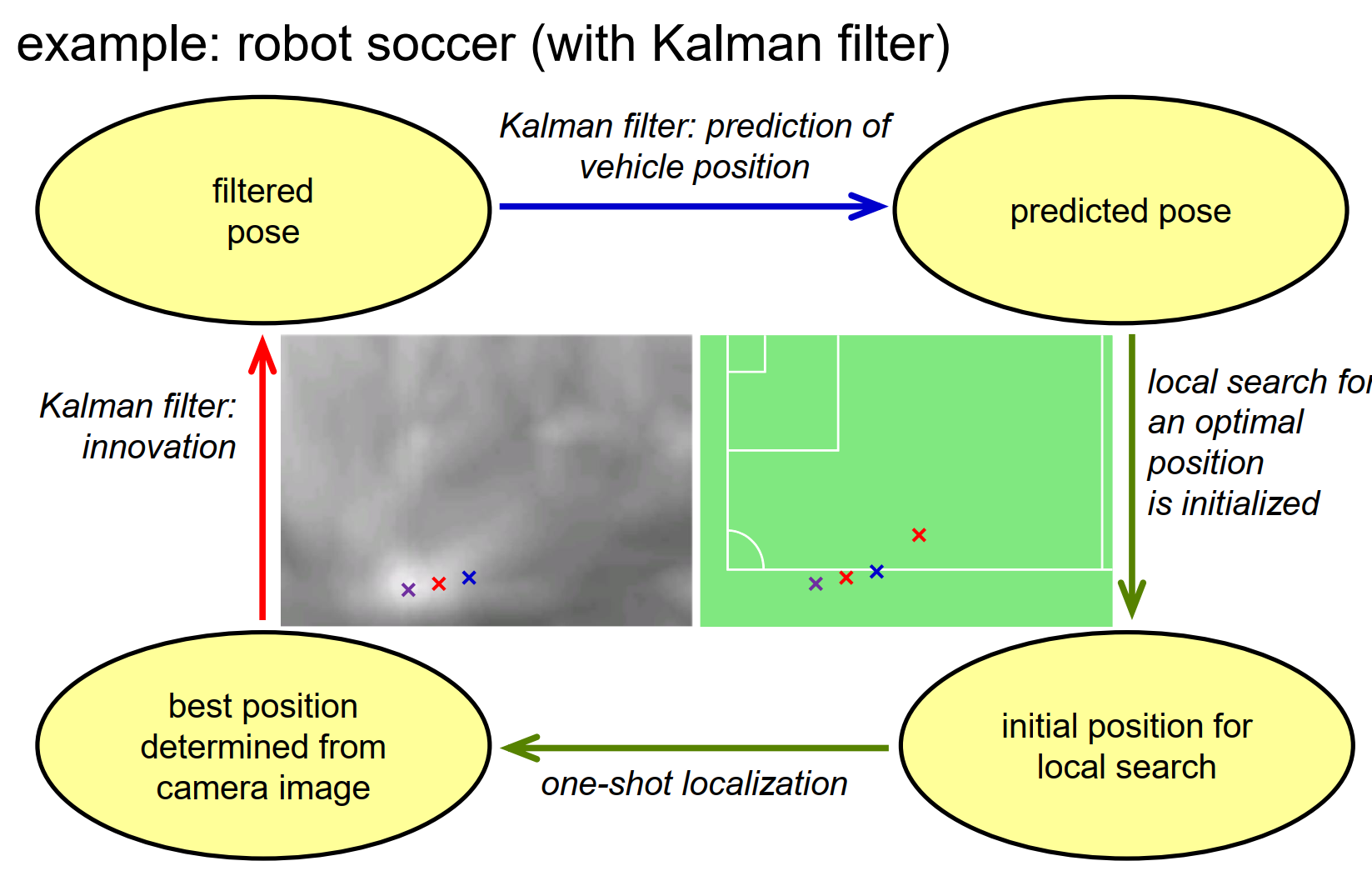
这个方法工作得相当好，这里有一个例子，一个非常简短的序列，显示了在这个机器人足球环境中的工作方式。你会看到这个机器人的符号是青色的，然后有四个圈，实际上一个圈标注为old，这是以前的位置，然后有一个标为odor的圈，这是预测的位置，然后有一个标注为dis，并且有一个紫色圈包围的圈，这实际上是通过匹配观察到的场地标记和地图确定的位置，然后第四个是一个标注为filter的圈，这实际上是创新步骤完成后的位置。所以现在这个图像是循环的，我们可以看到这些位置随着时间的推移是如何演变的。过滤器在一段时间内对观察到的东西进行了一些平滑处理，所以整个位置不会像我们只是考虑通过匹配观察到的场地标记和真实场地标记确定的位置那样跳动。这是一个关于位置估计方法的例子，我们可以看到这些位置如何随时间演变。滤波器在一定程度上对观测结果进行平滑处理，使得整个位置不会像仅考虑与真实场地标记匹配的位置那样跳跃。

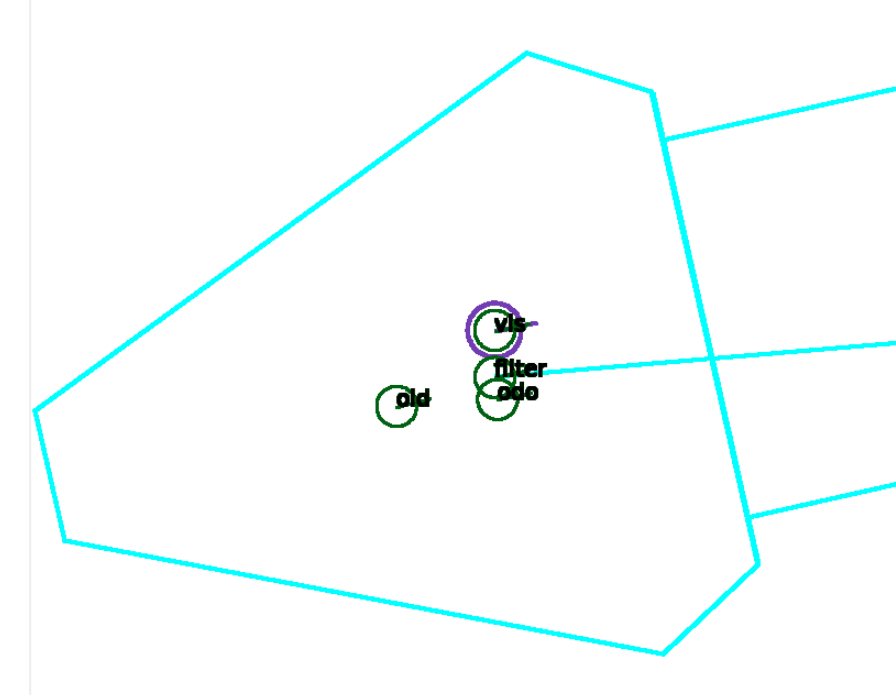
下面是一个更大序列的方法示例，其中观测到的场地标记也投影到摄像头图像中，并用青色曲线进行追踪。视频循环播放多次，我们可以看到尽管机器人进行了非常复杂的运动，该方法能够很好地跟踪这种运动，并能够很好地确定机器人的位置。这是这些技术在机器人应用中的成功应用，表明这种技术非常有用。

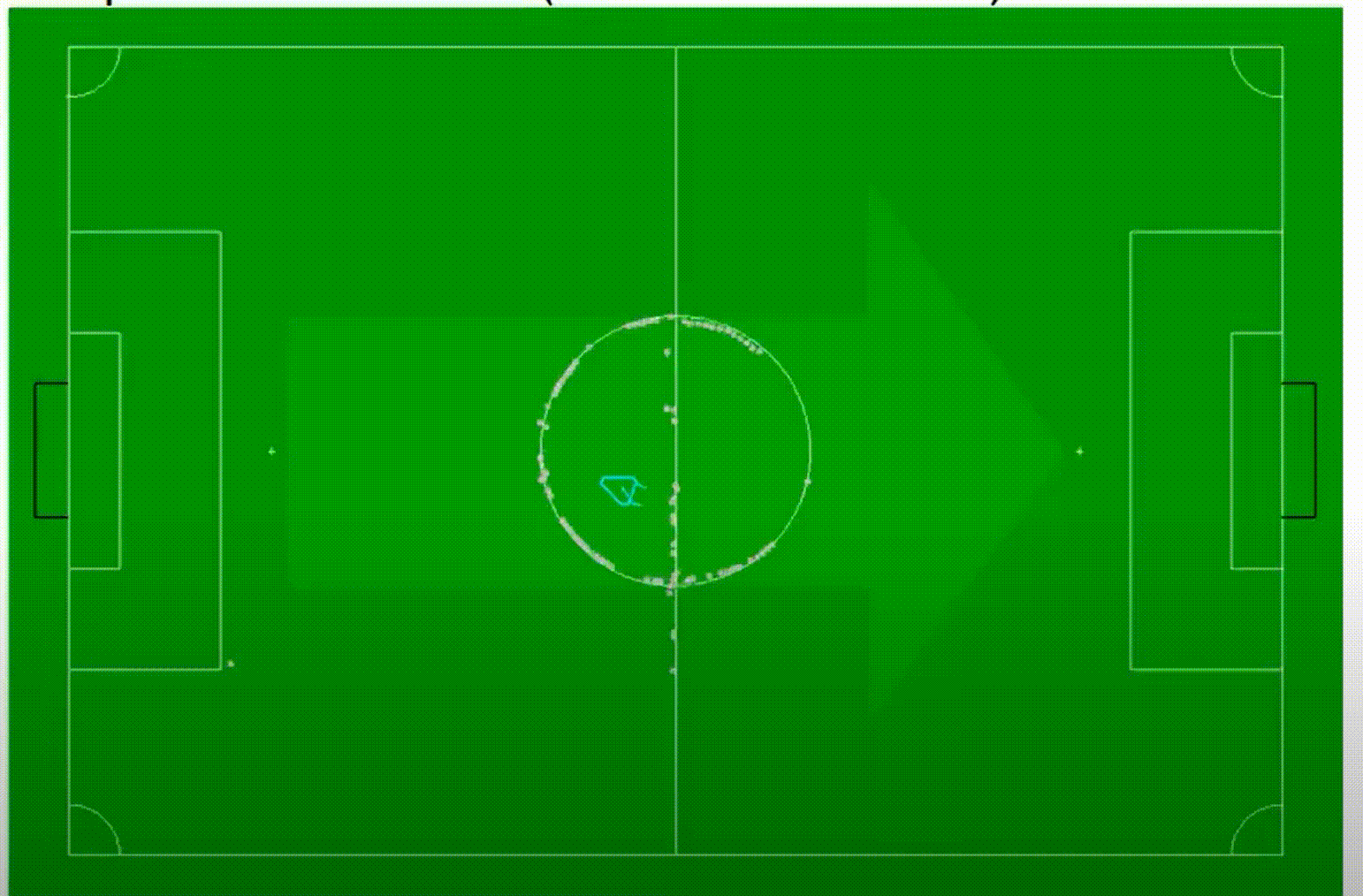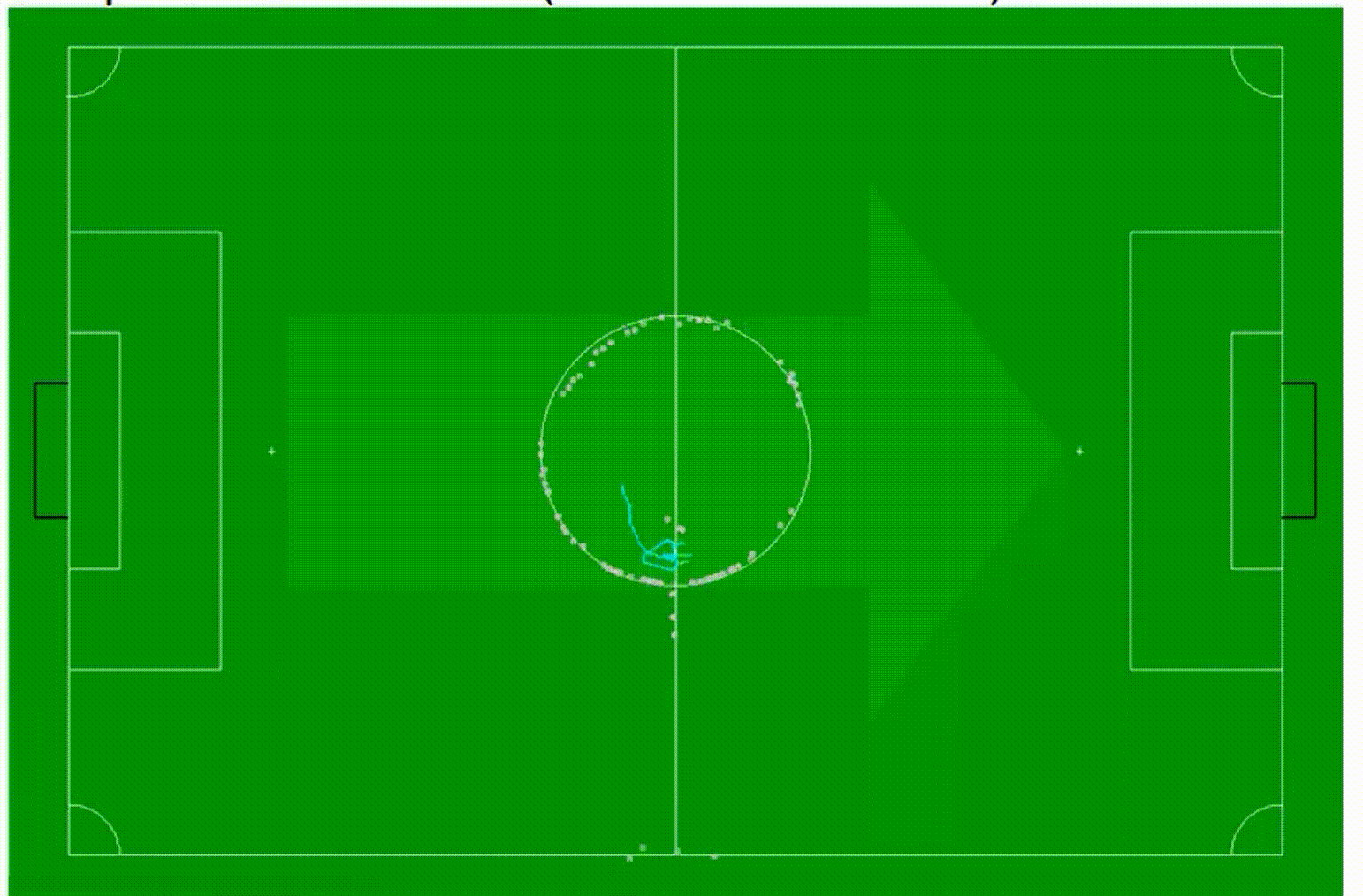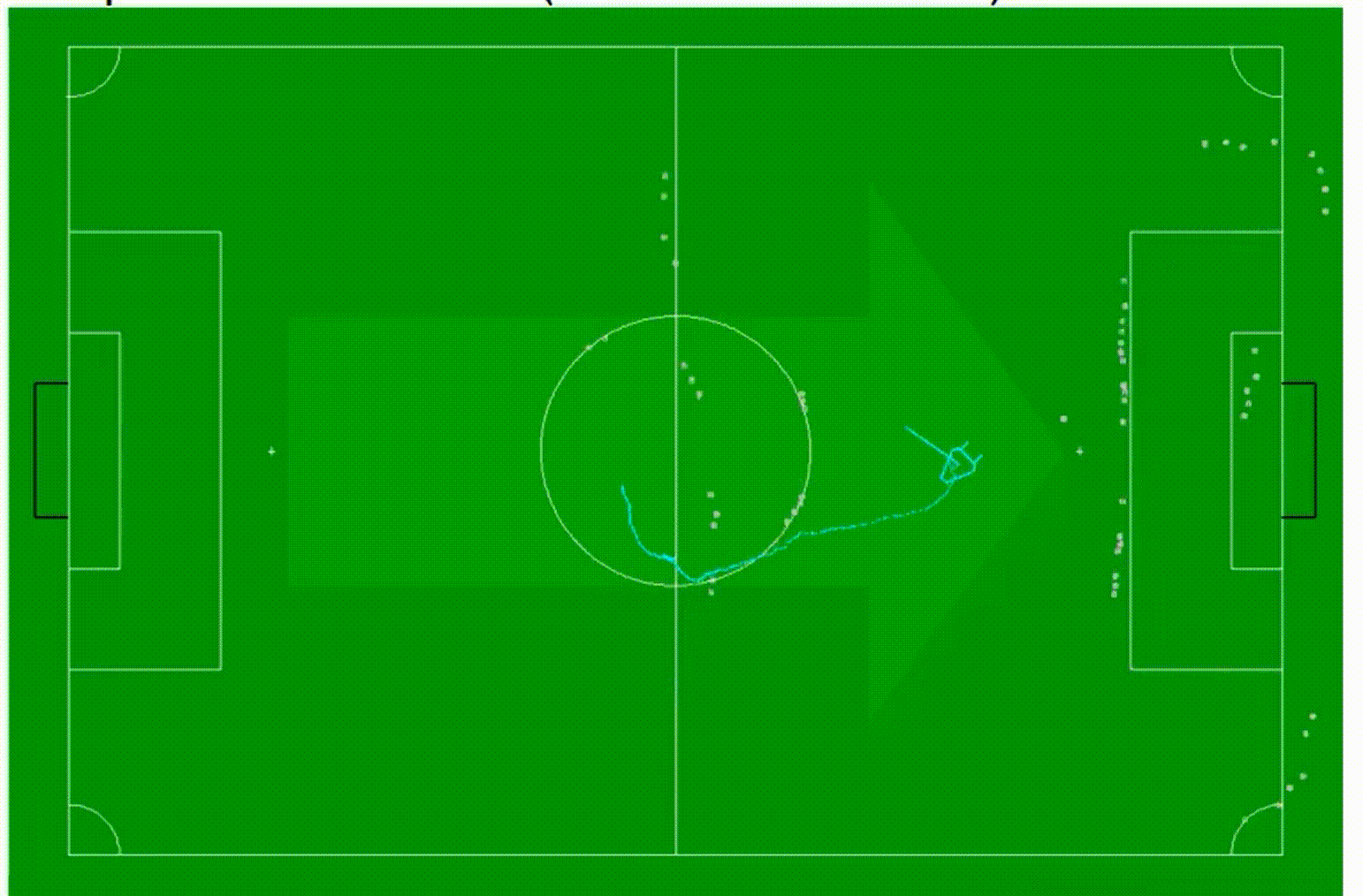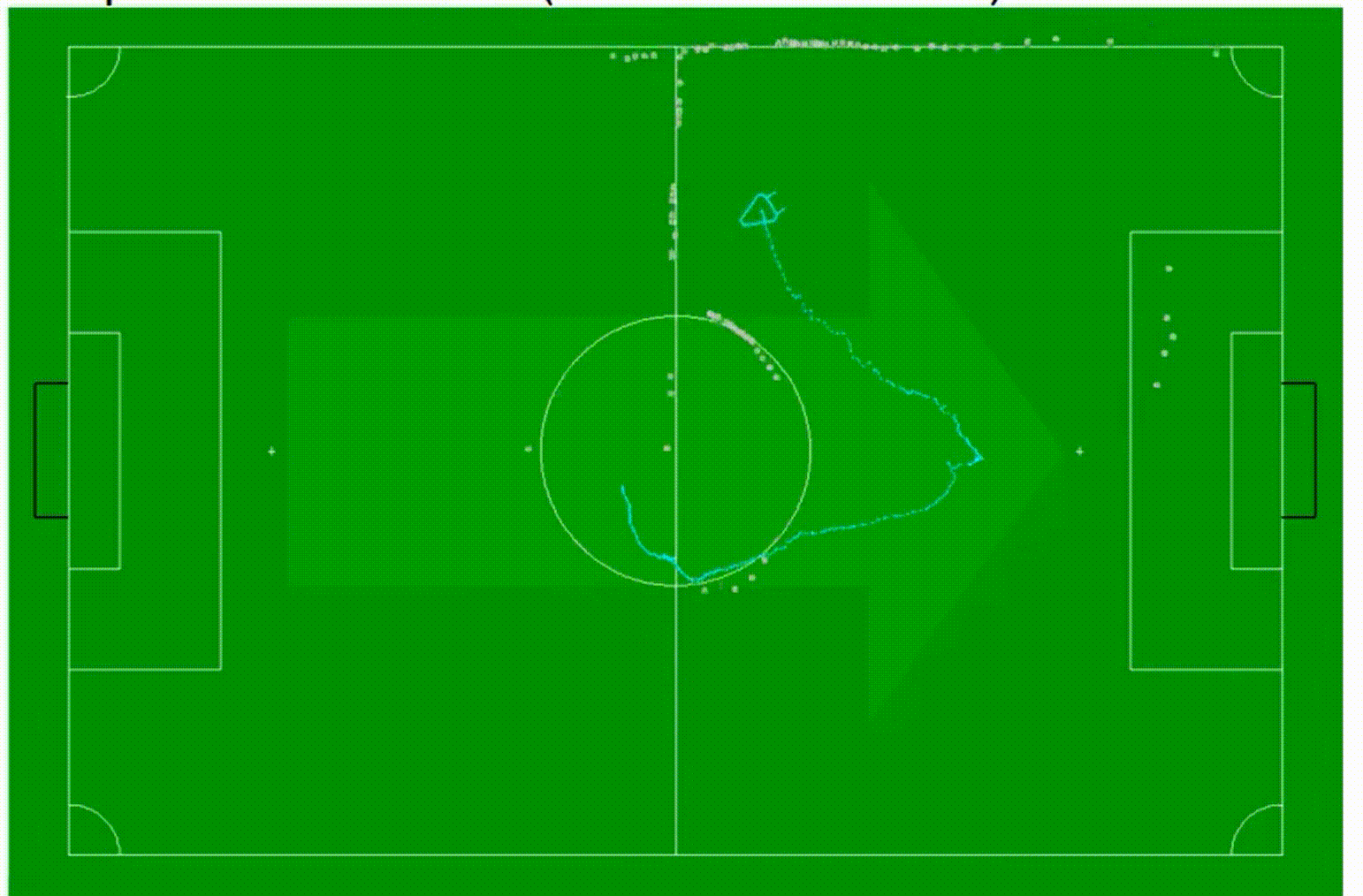
除了使用卡尔曼滤波器来模拟自我位置估计过程的想法之外，我们还可以使用粒子滤波器。粒子滤波器具有一些优点，也有一些缺点，但在这种情况下它也有一些优点。在这种情况下，我们会再次认为状态向量只是模拟机器人的当前位置和方向，这意味着其粒子模型是可能的车辆姿态。每个粒子当然也带有一个重要权重。在预测步骤中，我们只需将自我运动添加到每个粒子上，并添加一些噪声以考虑状态转移模型中的不确定性。创新步骤中，我们只需将粒子的位置和方向视为真实的机器人位置，将所有观察到的线点投影到世界坐标系中，并计算到最近真实线的距离。这意味着我们只计算当前位置和方向以及当前测量值与场地标记模型匹配程度的误差项，基于此来增加或减少粒子的权重。对于匹配程度很好的粒子，其权重增加，对于误差很大的粒子，权重减小，然后我们进行重采样步骤。通过这样做，我们逐步估计机器人的位置。当然，我们必须返回一个单一的位置和一个单一的方向，而不是一整套数值，但我们可以通过计算粒子的加权平均值来做到这一点，以确定机器人的平均位置或平均方向。正如我们在这里看到的那样，这也是有效的。我们有很多粒子，每个粒子用一个圆表示，圆的半径表示权重，圆内的线表示机器人的方向。 这个案例中使用500个粒子很好地工作。

使用粒子滤波器的车辆定位方法的例子是由乌尔姆大学的亨德里克·德意志开发的。他在他的博士论文中使用了这种粒子滤波技术，并将其用于自动驾驶车辆的自我定位。

想法是利用摄像头检测到的车道标线进行自我定位。车道标线是地标，但只有虚线部分，他通过某种方式计算出虚线车道标线的中心点，并将其用作地标。此外，他还使用了沿路的道路标杆，这些标杆是由激光雷达传感器检测到的。然后使用粒子滤波器来估计车辆的位置。这里是他记录的一个视频。下一部分中我们将看到的是前置摄像头的图像，在图像中我们可以看到一些黑色点，这些点是摄像头图像处理记录下来的点。

通常来说，这些误差通常小于一度。

现在我们可以放大视野，以便更详细地观察粒子云随时间的变化。

总的来说，我们可以看到整个方法在很好地工作。

我们可以利用这种技术在农村道路上进行定位。

Kidnapped Robot Problem

尽管这些增量定位技术非常有用，但当我们失去对当前位置的追踪时，就会遇到麻烦。也就是说，当我们不知道自己在哪里时，我们的先验知识就会变得非常糟糕。这通常发生在刚开始时，当机器人还不知道自己在哪里时，必须确定第一个位置，或者例如当感测到的自我运动与实际自我运动非常不同时，预测步骤中我们将得到一个与实际姿势非常不同的预测姿势，这可能会导致我们陷入一个局部最优解而不是全局最优解，或者在给定的时间间隔内，我们从机载传感器中获取不到足够的视觉信息来确定位置。例如，如果在一段时间内没有地标可供我们观察，并且自我位置从真实位置漂移出去，那么我们就会迷失方向。这个问题被称为绑架机器人问题，因为它有点像你绑架了一个机器人，把它带到另一个地方，然后机器人必须知道自己在哪里。在这些情况下，我们需要的不仅仅是机器人位置的增量更新，而是需要进行全局搜索以找到最优位置，因此我们确实需要在机器人可能存在的整个空间中进行搜索。

据文献报道，粒子滤波器在解决这个绑架机器人问题时是有用的，至少在环境不太大的情况下是有效的。例如，粒子滤波器可能在足球场上定位自身，但在非常大的环境中是不可能的。这种技术的基本思想是在这种情况下重新初始化粒子滤波器的粒子，并在整个状态空间上使用均匀分布的粒子，即在所有可能的位置和方向上使用均匀分布的粒子。然后可以观察到，在一段时间后，粒子越来越聚焦于状态空间中的一些有趣区域，也就是一些有趣的位置和有趣的方向。这通常在几次迭代内发生。最后，最初分布在整个区域的整个粒子云在一个很小的区域内凝聚成为一个很小的点云，这是这些技术的基本思想。让我们看一个例子。我们开始时，将所有粒子均匀分布在整个足球场上，考虑均匀分布的方向。每个粒子用带有线条的深蓝色圆圈表示，线条表示方向，圆圈表示位置，根据粒子的权重计算出平均位置和平均方向，用青色机器人符号表示。基于此，我们将所有观测到的平面标记投影到这个映射或图像中，这是粒子滤波器的第一次创新步骤的结果。我们可以很容易地看到，大多数粒子并没有真正贡献，它们位于不太有希望的位置，而只有少数粒子仍然显示出有希望的位置和方向，这些位置和方向在这里具有非常大的半径。现在我们看看经过一步之后的情况，重采样步骤已经消除了那些不太有希望的粒子，只有那些看起来有希望的粒子幸存下来，并且基于它们产生了新的粒子。现在我们可以看到粒子在禁区角落的某个区域开始聚焦，而不是禁区边缘，一些粒子位于中心线旁边的两三个不同位置。现在它已经更好地适应了，正如我们在另一个迭代之后所看到的，粒子越来越聚焦于禁区线旁边的这个区域，靠近中心线的粒子数量越来越少。最后，所有粒子都集中在禁区线旁边的区域，并且我们可以看到观测结果与真实世界中的位置相吻合程度不错。这是使用粒子滤波器时通常观察到的情况，经过几次迭代，粒子已经聚焦在一个小区域和一组可能位置上。然而，在这种情况下，我们知道机器人的真实位置并不在这里，而是在那边。这意味着，由于粒子滤波器是一种随机化技术，蒙特卡洛技术，我们不能确定自己是否最终到达了真实位置，也可能是一个局部最优解，而不是定位任务的全局最优解。这在很大程度上取决于我们使用的粒子数量。如果我们使用数百万或数十亿个粒子，那么我们最终不太可能陷入非最优的最小值，因为在开始时，这些均匀分布的粒子中有一个在正确位置的概率相当高，而如果粒子数量较少，那么当然这些粒子无法填满整个状态空间，这意味着在状态空间的相关区域中可能没有粒子存在，这时粒子滤波器非常有可能集中在错误的局部最优解上。

Mapping 映射

我们之前讨论了自定位问题和地图的表示。现在我们将介绍不同类型的地图、它们适用的场景以及如何使用它们。在机器人技术领域，地图是一个广义的概念，有许多不同类型的地图。下面是我们将要介绍的地图类型：

1. 点云地图：简单地存储2D或3D点的坐标，可以包含纹理信息。通过从立体相机或激光扫描仪收集3D点并将其排列在地图中创建。存储空间高效，只需要存储每个单元格是否被占用的布尔变量。

2. 特征点地图：仅存储有意义的特征点，如角点、边缘等。这些地图更加紧凑，可以通过跟踪关键点的方式进行更新和维护。

3. 占据栅格地图：将环境划分为规则的网格单元，每个单元格表示是否被占据。这种地图适合用于路径规划和避障，但可能对于感知细节不够准确。

4. Stixel地图：将图像分割为垂直柱状物体（stixels），每个stixel表示一段连续的垂直视觉信息。这种地图适用于车辆导航和场景理解。

5. 几何地图：存储环境的几何结构，如墙壁、楼梯、家具等。这种地图通常用于高级任务，如导航和场景理解。

这些地图类型根据存储的信息类型、抽象级别、紧凑性和数据访问效率进行区分。它们在不同的应用中具有不同的用途和优势。选择适合特定任务的地图类型非常重要。

地图问题本身可以看作是定位问题的逆问题，我们已知机器人的位置，但要确定我们事先不知道的地标的位置。我们有一些机载传感器，用于测量我们看到或发送到的相关地标的距离或角度，现在的任务是创建一个地图。这个问题并不是真的很难，因此我们可以通过状态图来简单描述这个映射过程。假设我们从一个机器人开始，它位于某个位置，首先计算机器人的姿势，可能有一些观测定位技术可以实现这一点。接下来，使用机载传感器检测世界上的地标或物体，可以使用相机、激光雷达扫描仪或其他传感器。然后，我们需要将物体的位置转换为世界坐标系，使用已知的机器人姿势进行转换。根据这一点，我们可以将这些物体输入地图中，或者如果地图中已经存在这些物体，可以通过对这些物体的多次测量进行平均来过滤它们的位置。完成这些步骤后，我们继续移动机器人，稍微改变位置，计算新的姿势，检测新的地标或物体，将它们转换为世界坐标，并输入地图中，或者过滤地图中现有的物体并更新它们的位置，然后继续这样进行。这是一种非常简单或稍微复杂一些的方法，当然，详细来说，你可能需要花费很多时间来计算机器人的姿势，你可能需要花费很多时间来过滤物体的位置并获得好的结果，但基本思想是相当简单的。

存在不同类型的地图，根据存储在地图中的信息类型、存储信息的抽象级别、表示的紧凑程度以及不同应用程序中数据访问的效率来进行区分。在本讲座中将讨论的地图示例包括点云地图、特征点地图、占据栅格地图、stixel地图和几何地图。

Point clouds

让我们从点云地图开始，它们相对简单，只需在地图中存储2D或3D点的坐标，即一个仅包含2D或3D坐标的大型数据库。它们可以用纹理信息进行注释，例如，你可以存储一个点是亮的还是暗的，但这并不是必要的。地图是通过将立体相机或激光扫描仪的深度图组合在一起创建的，因此只需从这些传感器中收集3D点并将其排列在地图中。

以下是一个简单的示例，展示了这些地图在可视化时的样子。上图显示了一个植物园的一部分，下图显示了一个室内环境，其中包含一些机器人应用中的室内墙壁。这些图像是由奥斯纳布吕克大学的伊朗·赫尔茨巴赫研究小组提供的。

点云地图的优点是它们具有低级别的抽象，创建地图时不需要对原始数据进行太多处理，这意味着地图生成相对高效。但当然，缺点是你必须处理大量的数据，因为一个双目相机图像很容易提供一百万个点，激光雷达扫描可能会每次提供几千个点，所以你很容易得到几个GB的数据，你需要存储和管理。

下面是一个可视化此类地图的示例，该视频来自于我们团队的前博士生Andreas Geiger，他现在在图宾根大学。在这里，你可以看到这样一幅图片，这样一幅地图是什么样子的，如果你使用从相机的双目设置中记录下来的点进行可视化。

Feature point maps

比点云地图更复杂一些的是特征点地图，实际上，它与点云地图相同，只是存储了特征点，比如 SIFT 或 SURF 等特征点方法，但这里不仅存储坐标，还存储描述符。这意味着你得到的是点以及每个点的标识符和描述符，你可以使用描述符来确定你看到的是哪个点。这在后续进行姿态计算或定位时非常有用，因为你可以使用描述符来识别你所观察到的点。

当然，抽象级别仍然很低，我们只是存储了points。

地图生成仍然是高效的，当然需要一些时间来计算这些特征点，但仍然是高效的。内存需求不像点云地图那么高，因为通常特征点的数量远小于从双目摄像头图像中获得的3D点的数量，例如。因此，点的数量不是很大，然而，你必须存储描述符作为额外的信息。特征点方法在自我定位方面特别有用，因为特征点可以用作地标。

Occupancy Grids

当我们使用占用格子地图时，进行了一些更高级的抽象。在占用格子地图中，我们将整个空间分割成不同的单元格，最简单的情况下，每个单元格具有相同的大小。

例如，如果要制作一张地面的二维地图，我们可以将该区域划分为一些正方形单元格，如图示所示。对于每个单元格，我们只需要记住是否在该单元格内观察到了点，或者我们认为该单元格是空闲的。因此，我们只存储或提供二进制信息，一个单元格可能被占用或为空闲，如图示所示，白色表示空闲单元格，深灰色表示占用单元格。这是一种非常高效的存储空间的方式，因此我们不需要存储数百万个点，只需要为每个单元格存储一个布尔变量，即一个或多个位的存储空间。

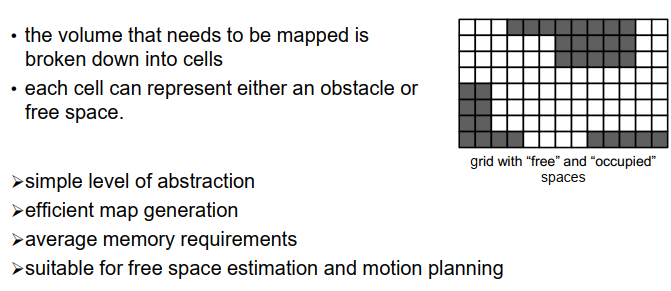
抽象级别并不太复杂，但在创建地图时已经进行了一定程度的抽象和信息累积，因此它并不像点云地图那样简单，但也还没有像后面将要看到的一些地图那样复杂。地图的生成仍然是高效的，虽然不像点云地图那样高效，但仍然是高效的。内存需求在某种程度上是平均水平的，这是一种非常适合自由空间估计和运动规划的地图类型。如果我想规划一个机器人从A点到B点的移动路径，我需要找到一条只通过空闲单元格而不进入较暗的占用单元格的路径，因此对于这个目的来说，这种占用格子地图是有用的。

我们如何创建这些占用格子地图呢？思路如下：假设我们有一个初始的空间单元格划分，如图所示，对于每个单元格，我们初始化两个计数器，一个计数器用于统计单元格内的点数，另一个计数器用于统计我们在单元格后面观察到点的次数，也就是说，我们的传感器（无论是激光还是摄像头）通过该单元格时，有多少次没有击中单元格内的点。

在这种情况下，我们可以假设相机或传感器位于底部中心，如图所示，我们观察到了红色的点。现在，我们考虑传感器所经过的所有线条，得到了虚线。这些是传感器所跟随的视线。现在，我们可以计算每个单元格有多少条视线经过，并有多少点位于单元格内，也就是说，有多少条视线结束于某个特定的单元格。然后，我们可以决定，例如对于那些现在显示为深蓝色、单元格内有点的单元格，我们可以说这些单元格是占用的，而且对于其中一个单元格，我们甚至找到了两个点，所以如果在一个单元格内找到了两个点，也许我们更加确定单元格内确实有一个物体存在。还有一个单元格，我们在其中找到了一个点，并且还有一条通过该单元格的视线，你可以看到该单元格不完全被深蓝色填充，而是显示了一些黄色和蓝色的条纹，这是一种冲突的单元格，我们不确定其中到底发生了什么，它可能被阻塞，也可能是自由的，也可能是该单元格的一部分被阻塞了，我们不确定。

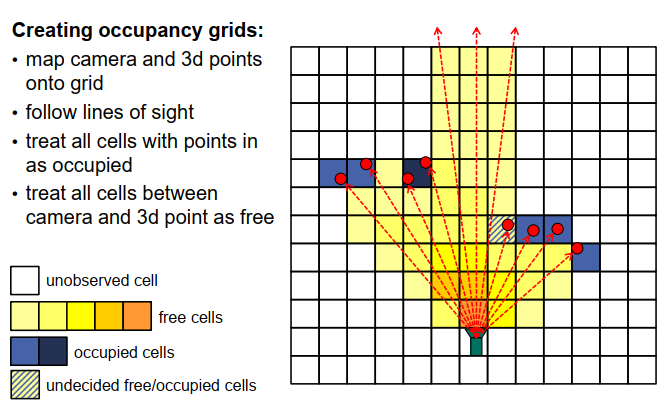
让我们来看看黄色单元格，在这些单元格中，我们发现了一定数量的视线通过而没有击中物体，对于这些单元格，我们比较确定它们是空闲的。

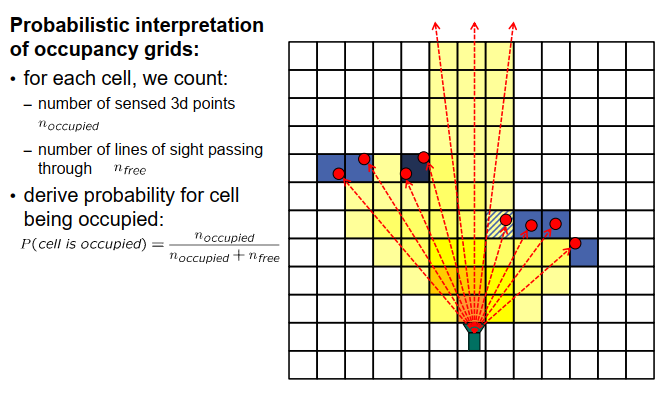
通过这种方式，我们计算每个单元格经过的视线数，以及单元格内发现的物体点数，因此我们有两个计数器，并根据这些计数来决定单元格被占用的可能性有多大。其中一种经典的方法是假设我们有计数器计算物体点的数量（称为n_occupied）和经过的视线数量（称为n_3），现在我们可以估计单元格被占用的概率。一个简单的情况是将被占用的概率定义为 n_occupied / (n_occupied + n_3)。

有时候，占用格子地图会占用过多的内存，特别是当处理非常大的区域时，可能有许多单元格相对不那么有趣，要么全部被阻塞，要么全部为空闲，此时将整个空间细分为非常小的单元格可能不是正确的方法。在这种情况下，更高效的表示占用格子地图的方法是使用一种称为四叉树或八叉树的技术。对于二维区域的地图，使用四叉树，对于三维空间的地图，使用八叉树。在这种情况下，我们将空间划分为单元格，但单元格的大小会稍微有所变化，所以我们可以将小单元格组合成较大的单元格，只要它们全部被占用或全部为空闲，这样可以减少需要存储的单元格数量。

在左边，我们看到了一个具有相同大小的单元格的规则占用格子地图，所有单元格都具有相同的大小。右边我们看到了四叉树（quad tree），它对应着相同的情况。如我们所见，单元格的大小是不同的。在那些所有小单元格中，它们在同一区域内共享相同的信息，要么全部被占用，要么全部为空闲。这样可以减少我们需要存储的单元格数量。

我们如何创建这些四叉树呢？通常情况下，我们以一种增量的方式开始，从一个覆盖整个空间的大单元格开始，该单元格可能部分被占用，部分为空闲。如果我们发现它既被占用又为空闲，那么我们也可以说存在冲突。我们开始将这个单元格分割成四个相等大小的子单元格，通过水平和垂直线进行一次分割，如底部一行所示。现在，我们检查每个子单元格，看它们是部分被占用还是部分为空闲，或者完全为空闲或完全被占用。如果它们完全为空闲或完全被占用，我们保留这些单元格不再分割。例如，在这个例子中，右下角的单元格完全为空闲，所以我们保留这个单元格，不再分割。对于其他三个单元格，我们发现它们部分被占用，这意味着我们继续分割这些单元格，直到再没有需要分割的单元格，或者达到我们不想再分割的最小单元格大小。

这是一个二维格子地图的情况，我们将这样一个正方形总是分割成四个子单元格，如你在这里看到的。在三维的情况下，我们处理的是立方体，如果我们想要分割一个立方体，我们将其分割成八个不同的立方体，然后称之为八叉树（OCT tree）。四叉树和八叉树的优点是存储可以以更高效的方式完成，我们不需要保存太多的信息，并且可以将没有不同信息的区域组合在较大的单元格中。

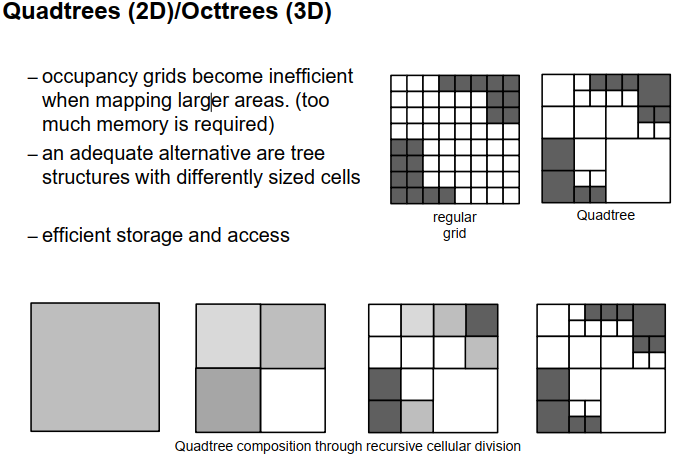
占用格子地图的另一种变体是所谓的2.5D地图或高度地图（height map）。在这些2.5D地图中，我们不仅存储一个单元格是否被占用，还存储了该单元格中最高物体点的高度。因此，我们可以存储在单元格中发现的障碍物的高度。在这里，我们看到了一个例子，我们将二维地面划分为不同的单元格，然后对于每个单元格，我们知道其中的最大高度的物体，通过这些柱状图的高度表示。我们得到了一种阶梯函数或阶梯世界，代表了环境。

与占用格子地图相比，2.5D地图的优点在于在高度方面有额外的信息，例如，我们可以区分区域中是否只有一个小的障碍物，我们甚至可以穿越它，或者该物体很高，我们无法通过它。因此，我们可以区分是只有一个小的路缘石可以跨越，还是有一些较高的物体完全无法跨越。抽象级别并不比占用格子地图高很多，当然，创建这些地图仍然是高效的，内存需求与占用格子地图类似，唯一需要考虑的问题是如何模拟悬挂障碍物，例如悬挂在道路上方的三个树枝，或者铁路道口的障碍物，如何表示它们有点困难，我们需要决定是完全忽略这些对象还是将它们表示为从底部到某个高度的对象，这是一个更复杂的问题。

Stixel Map

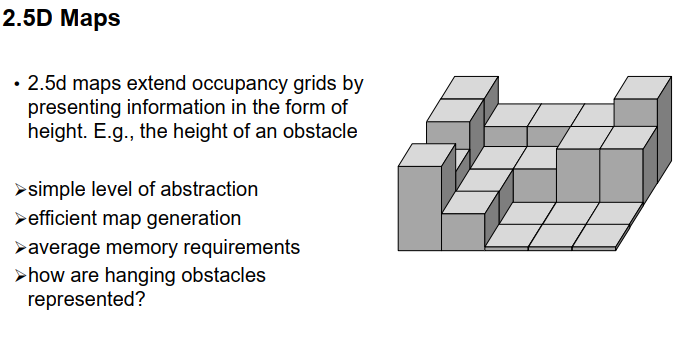
2.5D地图的另一种变体是所谓的stixel地图，这是一个主要在戴姆勒公司开发的自动驾驶领域的特殊发展。这些像素地图也可以被看作是一种2.5D地图，但所使用的网格地图是以极坐标而不是欧几里得网格来表示的，并且它们非常依赖于双目视觉技术。这些技术使用双目视觉来首先估计车辆前方的自由空间，并估计与该自由空间相邻的所有对象的高度，然后为这些对象生成一些柱状体，而在这个上下文中，这些柱状体被称为stixel。stixel是将stick（棍子）和pixel（像素）结合起来的人工词汇，所以就是stixel。在右边的图像中，我们可以看到一些图像，顶部的图像是场景的双目重建图像，这是一个颜色编码的视差图像，下面的图像显示了这个示例的stixel表示，颜色以某种方式对对象进行了分组，可以看到对象是由这些像素表示的，而车辆前方的自由空间则以自由空间表示。

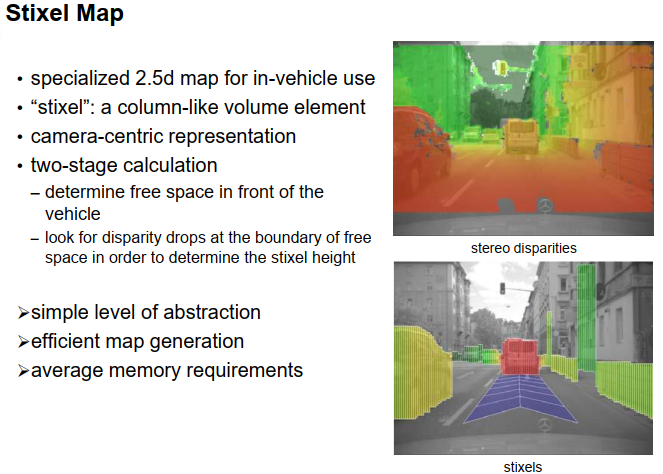
是的tixel就是一种类似柱状的体积元素，它使用以摄像机为中心的表示方法，计算分为两个阶段。首先，我们确定摄像机前方的自由空间，然后在自由空间的边界上寻找视差降落以计算stixel的高度。抽象级别仍然类似于2.5D地图，它特别适用于双目图像处理，效率或多或少高，内存需求适中。

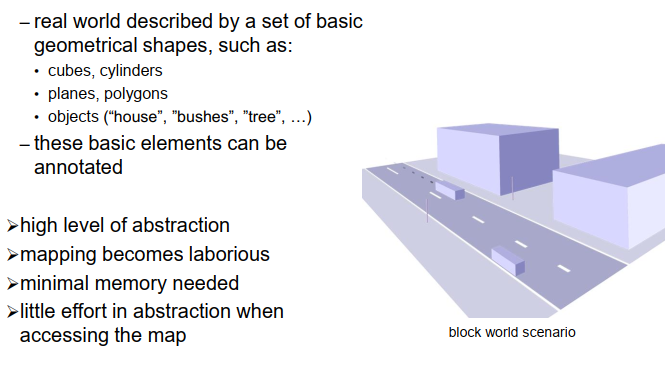
除了这些地图之外，我们可能还可以尝试创建比以前更高级、更抽象的地图，不仅仅是创建单元格或点，而是以几何形状和几何基元来表示世界。例如，你可以用立方体、圆柱体、平面、多边形和物体来表示世界，并存储这些信息片段，而不仅仅是点或点云。那么，世界可能看起来像这样，由描述环境的这些平面、圆柱体、多边形等构成。

这些对象也可以进行注释，也就是说，你可以说这是一座房子，这是一个交通标志的柱子或其他。这样，你就获得了比仅存储几何信息更高的抽象级别。

Geometrical Map

是的，我们有很高的抽象级别，当然绘制这种地图会比较费力，你需要进行很多工作来创建这些地图，可能需要估计几何形状，进行一些语义分析，确定哪些部分属于一起等等。但当然，与其他地图相比，内存需求要小，因为环境中的物体数量通常要比表示环境所需的点或单元格的数量小得多，当然，在创建地图时花费的工作量是可以在以后使用这些信息时节省的。这取决于应用程序，所以如果你在应用程序中想要知道你面对的是哪种对象，那么如果你的地图中有标记的对象，那当然非常有用；如果你对此不感兴趣，那么也许并不重要。我认为这些几何地图在许多应用中都很有用，并且比简单的点云地图允许更高级别的推理。

这是我们讨论的不同地图类型的概览，从点云地图、特征地图到占用格子地图和四叉树/八叉树，再到2.5D地图和stixel地图，它们还表示物体的高度，最后是几何地图。

从上到下，抽象级别逐渐提高，但创建地图的工作量也相应增加； 从下到上，内存需求增加，读取地图和使用地图的工作量通常也增加。

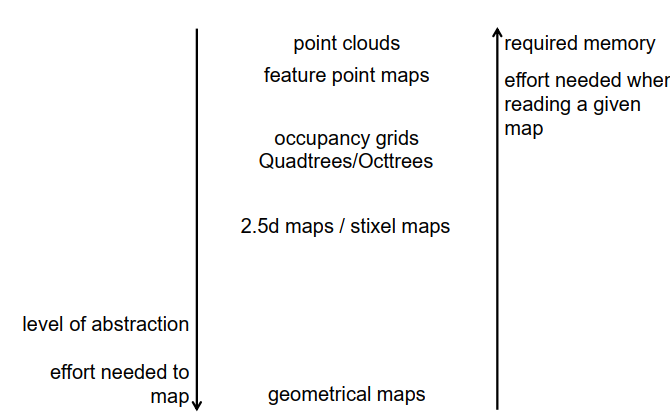
Example 为了更好地了解和理解不同类型的地图以及表示世界的不同方法，让我介绍一下我们团队以前的一个项目。该项目旨在帮助盲人和视觉障碍者在陌生空间中导航。我们使用了一套安装在头盔上的双目摄像机系统，盲人或视觉障碍者戴着这个头盔。图像被计算机分析，然后相关的信息，如障碍物位置或目标位置等，通过声音编码进行编码，以便视觉障碍者能够听到他们无法看到的相关信息。图片显示了我们在该项目初期使用的实验设置，一个带有双目摄像机的头盔，一个笔记本电脑，一个电池和一个游戏手柄，用于开始和停止记录数据。基于此，我们在卡尔斯瓦尔德（Carlswald）行走并记录图像序列，然后根据这些图像序列来开发分析环境、提取世界信息、描述世界和创建抽象表示的算法。

第一种方法是基于创建环境的几何地图的想法，这是通过提取建筑物的平面并用平面或平面的部分来表示它们来实现的。图片显示了一个示例图像，绿色像素被分配给地面平面，所有标记像素都被分配给右侧所示的垂直平面，用宽框表示。

另一种方法是基于占用格子地图的思想。图片展示了一个示例结果，右下角显示了俯视场景的占用格子地图的示意图。黑色单元格表示我们不知道它们是否被占用，红色单元格表示被占用，红色颜色的饱和度越高，表示该单元格被占用的可能性越大，白色单元格表示空闲单元格。有时会出现蓝色单元格，代表所谓的负对象，即地面上的洞或向下的楼梯，这对盲人或视觉障碍者来说也可能是危险的事物。右侧的绿色线表示投影的垂直平面，即左下图像中我们看到的平面的位置。

中间的图片还说明了占用格子地图，我们将每个像素点与占用格子地图中的颜色对应，所有显示为红色的像素都被视为障碍物，而非红色的像素被视为自由空间。

让我们先看一下视频序列，首先我们来看平面估计，我们将在左上图像中看到原始摄像机图像，右上图像是视差图像，颜色编码了每个像素的视差，红色表示近，蓝色表示远，黑色表示无法估计视差值。左下图像显示了估计出的平面，每个平面用特定的颜色进行编码，即共享相同颜色的像素被假定属于同一个平面，垂直平面也用宽框表示，白色数字是平面的标识号和该平面已被跟踪的帧数，右下图像显示了一种类似于2.5D的场景表示，每个像素表示其相对于地面平面的高度，红色表示高于地面平面，蓝色表示低于地面平面，饱和度较高的灰色表示大致位于地面平面上的部分。

让我们开始播放视频，看看发生了什么。我们可以看到，在这个例子中，我们能够跟踪到一个或两个垂直平面，一个是左侧的建筑物平面，有时也会出现对面的建筑物平面。有时候，一些列或物体的部分被误分类为墙壁。左手边有一个稳定的墙壁，有时候很难估计这些墙壁，因为商店的窗户可能无法产生有效的视差，从而可能会误导算法。再比如，电车也被识别为墙壁。我们并没有对物体进行任何语义分类，所以我们无法明确指出这是一辆电车，只是觉得这有点像墙壁，于是在我们的表示中，它就变成了一堵墙。

现在我们估计出的平面就是这样。接下来，我们来看一下对于之前看到的同一视频序列的世界的占用网格表示。在左上角的图像中，我们看到了我们之前估计的平面，绿色表示地面平面，其他所有颜色表示其他不同的垂直平面。在右侧，我们看到了占用网格的顶视图。在中心，我们看到了橙色的圆圈，这是自我位置，黄色的线条显示了当前的观察区域。然后，绿线显示了观察到的垂直平面的投影。

我们四处走动，绘制出所有的障碍物。当我们穿过马路时，这里有很多的空地。有时候你会看到这些蓝色的区域，它们是负障碍物，但在这个情况下，这些更多的是人为因素造成的。大部分的蓝色区域是由错误的视差图像生成的，它们之所以错误，是因为它们是在窗户中创建的，基于反射。因此我们得到了这些人工的蓝色区域。我们看到的，某种程度上是合理的。当然，我们不能区分移动的物体、空地和静止的物体，因此，车辆或行人的移动也会生成一些红色的单元格。这里出现了一些问题，地面平面不再被很好地估计，因此它有些倾斜，因此垂直平面和占用情况也被错误地估计，所以我们看到了这些人为因素。

如果我们前方只看到一小部分地面平面，那么估计地面平面就不那么容易了。在开发的后期阶段，我们也使用了惯性测量单元，这在稳定这些估计上非常有帮助。它也提供了地面平面的一些正常向量，这有助于稳定地面平面的估计。但是你在这里看到的视频，只是用摄像机信息录制的，没有使用惯性测量单元，没有其他的东西，没有GPS或者什么的，只是考虑到你刚刚看到的视频序列。所以这里的一切都是基于视频的。

你也可以看到，有时候平面估计并不那么好，如果墙壁离得很远，比如20米远，因为这样视差当然也就不那么准确了，然后估计这些平面的方向就比较困难了。再次，地面平面被误估计，然后整个方法都不管用了，我们需要重新设置整个方法。

Simultaneous Localization and Mapping(SLAM)

在第六章的最后部分，我们想结合我们到目前为止学到的技术，即自我定位和映射技术，这会产生一种叫做同时定位和映射的技术，简称SLAM。这个想法是我们从一个空白的地图开始，我们不知道机器人的位置，也不知道地标的位置，我们逐步构建地图，估计车辆或机器人的轨迹。这可以通过下面的图像来说明。在左边，我们看到真实的情况，是真实情况的顶视图，有四个地标A，B，C和D，还有一个机器人从蓝色圆圈指示的特定位置开始。地图是空的，没有地标，也没有机器人的姿态。然而，为了简化，我们假设机器人从地图坐标系的原点开始。这当然是一个任意的选择，我们也可以从任何其他位置开始，实际上这并不重要。现在，机器人使用其机载传感器感测到一些地标，并将这些地标加入地图。

然后，它继续移动，移动到第二个位置，它再次使用其机载传感器感测环境中的一些地标，例如在这个例子中的A，B，C和D。由于A，B和C已经是地图的一部分，它可以使用这些观测数据来确定机器人的位置。

当然，它可以将新的地标D加入地图，并可能更新地标A，B和C的位置，以减少测量中的噪音。

然后，机器人再次移动，在第三个位置，它再次感测到一些地标，比如B，C和D，根据这些，它可以确定自己的位置。这样的程序就继续下去。

我们可以用几何方式来模拟这个任务，描述不同未知变量之间的关系。有一些地标，由红色的小点表示，还有一些机器人的姿态，由蓝色的圆圈表示，还有一些机载传感器的测量值，提供了地标位置和机器人姿态之间的一些关系，这由实心箭头表示。此外，我们可能在机器人上装有一些传感器，使机器人能够感知它在两个姿态之间执行的位移，这由虚线箭头表示。这不是SLAM必需的，但是可能的扩展。

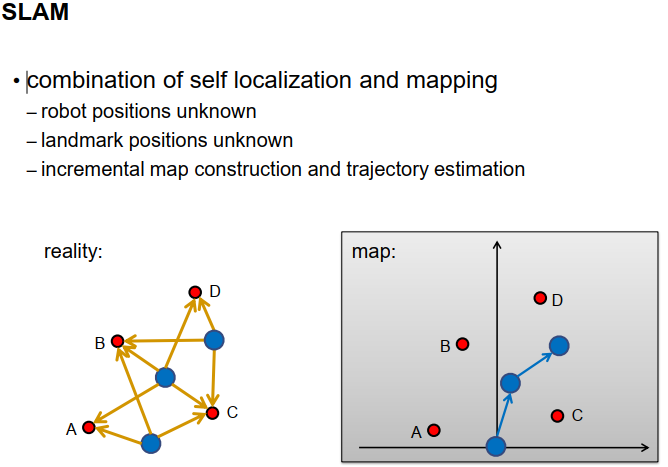
现在我们可以区分哪些变量是已知的，哪些需要估计。如果机器人的位置已知，只有地标的位置未知，那么我们处理的就是映射问题。如果地标的位置已知，但机器人的位置未知，那我们就在处理自我定位问题。如果两者都未知，那么我们就在处理同时定位和映射问题。

那么，我们怎样才能以算法的方式解决这个问题呢？这里的想法是使用一个增量估计过程。每当有新的观察结果，我们就进行一些更新，以更新未知变量，即地标位置和机器人位置。这可以使用我们已经熟悉的滤波技术来完成，例如卡尔曼滤波器。系统状态被用来表示未知变量，也就是地标的位置和车辆的姿态。状态转换实现了车辆从一个点到另一个点的位移，观察结果是相对于车辆坐标系统的地标位置。

现在让我们以更精确的数学方式来建模这个问题。未知变量是机器人的位置和方向，我们用位置向量X和方向角度Phi表示它在二维情况下。如果我们在三维情况下移动，我们需要一个三维位置向量X和三个方向角度，例如一个滚动、俯仰和偏航角度来描述这三个维度的方向。此外，地标位置也是未知的，这用带有索引k的Y来表示。状态向量因此由X、Phi和所有的Y向量组成。状态转换反映了机器人从一个时刻移动到下一个时刻的事实。我们在这里假设机器人的移动可以用机载传感器感知，例如用轮式编码器、视觉里程计或惯性测量单元，所以我们不需要在这个卡尔曼滤波器中去估计它。当然，如果稍微扩展一下，这也是可能的，但为了简单起见，我们不希望在这里这样做。所以我们假设有一些机载传感器提供了一些描述机器人相对位移的矢量Delta X和描述机器人方向变化的Delta Phi。有了这个输入，我们可以描述出新的状态向量就是X加上r Phi乘以Delta X，Phi加上Delta Phi，而所有的地标位置并没有改变。r Phi是一个相对于偏航角Phi的旋转矩阵，它在这里被用来将机载传感器在车辆坐标系统中感知到的向量Delta X转换到世界坐标系统。所以在这里，我们必须确保我们在正确的坐标系统中进行所有的计算。

观测值是地标，这意味着我们发送的是相对于当前机器人或车辆坐标系的地标的相对位置，实际上是向量 y_i - X。然而，y_i - X 是世界坐标系中的向量，因为相对位置是由机载传感器感知的，测量本身是以车辆坐标系表示的，因此我们需要将 y_i - X 转换为车辆坐标系，可以通过应用旋转矩阵R的逆矩阵或转置矩阵 RFI 来实现。对于每个观测到的地标，我们得到一个观测方程，如下所示。正如我们所见，观测方程依赖于旋转矩阵R，其中包含余弦和正弦项，这些项是非线性函数。由于 Phi 是一个状态变量，状态向量和观测之间存在非线性关系，这意味着如果我们想要估计状态向量，就不能使用常规滤波器，因为观测方程不再是线性的。然而，我们可以使用扩展卡尔曼滤波器或无损卡尔曼滤波器来估计这个向量。

让我们看一个简单的示例，介绍一下这种称为 EKF SLAM 的技术如何工作。我们假设在二维平面上进行移动，左侧是实际运动，机器人在一个规则的圆上移动，这个区域中有一些地标，大致随机分布，用红色十字表示。机器人从圆的最右侧位置开始。右侧是一个视频，显示了地图和估计轨迹的演变。每个估计的地标位置用红色十字和描述不确定性的协方差椭圆表示。椭圆越大，对该位置的知识越不确定，椭圆越小，我们对其越确定。初始机器人位置假设为完全已知，然而，机器人的移动当然会有一定程度的不确定性。现在让我们开始播放视频，看看地图如何随时间演变。

红色地标是机器人当前感知到的地标，蓝色地标是机器人当前无法感知到的地标。机器人的姿态由黑色圆圈表示，圆的半径与我们对机器人位置的不确定性有关。 当机器人一段时间内无法感知到地标时，我们可以看到其位置的不确定性增加，而如果它再次观测到之前看到过的地标，其位置的不确定性会减小。我们还可以看到如果一个地标被多次观测到，其不确定性会减小，对地标位置的不确定性减小。

在这个序列中，有一个非常有趣的点，一段时间后，机器人几乎完全绕了一圈，但只是差一点。它从右边开始，然后沿着圆圈逆时针移动。在那个时间点上，我们可以看到机器人的位置并不那么准确，机器人位置的不确定性很大，地标位置的不确定性也很大，因为在前面的路程中，机器人运动的不确定性已经累积起来，所以一段时间后，机器人位置的不确定性很大，这也意味着地标位置的不确定性很大，这些地标添加到地图中。在下一步中，机器人将再次看到第一个地标，它在开始时已经看到过，当时机器人位置的不确定性非常小，发生了什么呢？

我们可以看到，现在机器人位置的不确定性大大降低，而且沿途地标位置的不确定性也已经降低，即使它们当前没有被机器人看到，不确定性也已经降低。这些所谓的回环闭合在SLAM中非常重要，可以获得高度准确的地图。如果没有回环闭合，地图将逐渐偏离实际情况，而有了回环闭合，要获得一致的地图就容易得多。

在这一点上，我想介绍一种SLAM的应用示例，这是由Henning Latigan在他的博士论文中开发的，并且后来成立了一家公司并且进行商业化。他的目标是基于立体摄像头系统为自动驾驶车辆实现自我定位和地图制作，这意味着只有在制作地图时我们使用了立体摄像头系统，而后来在定位时只需要单目摄像头就足够了。在这里，我们看到了实验车辆的简要图像，车顶上有一些摄像头。下面是一些图像，它们是用后置摄像头拍摄的。他的工作中的想法是使用图像中的特征点作为地标，图像显示了一些橙色圆圈作为这些特征点，圆圈的半径表示它们被发现的尺度。我们可以看到在城市环境中，我们很容易在环境中找到几十个或上百个特征点，通常是建筑物上的特征点，车道标线上的特征点，植被上的特征点，道路表面上的特征点较少。

制图是利用双目摄像头系统和SLAM方法完成的。双目摄像头系统用于三角测量特征点的位置并将其添加到地图中。

随后的自我定位仅使用单目摄像头进行，这并不困难，因为我们有很多地标，因此只使用单目摄像头而不是双目摄像头也是可能的。当然，双目摄像头可以提供更多信息，也许可以进一步改善结果，但对于这种方法来说，单目摄像头已经足够。

整个方法都没有使用任何额外的传感器，所以没有使用GNSS，也没有使用IMU传感器，只用了摄像头。

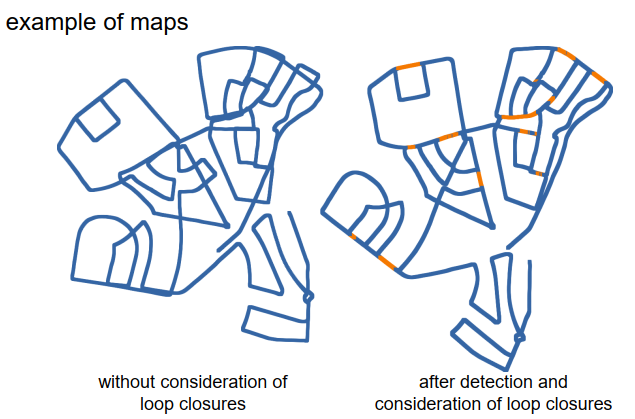
这是使用该SLAM方法创建的地图的一个示例。左侧显示了一个在不考虑回环闭合的情况下创建的地图的一部分，这意味着假设每个被观察到的地标要么是在几张图像之前就已经看到过，要么是之前从未看到过。即使是那些同一条道路被多次行驶的区域，我们也没有关联地标。结果显示在左侧，我们可以看到事物并不完全匹配。可以很容易地看出，某些地方道路已经行驶过多次，但估计的地图并不吻合。 考虑到回环闭合后，右侧显示的地图效果好得多。回环闭合对稳定地图估计有很大帮助。与城堡的实际地图进行比较，你会发现它相当匹配。在这个例子中，如果你想尝试一下，这是部分映射的Ripple。

下面是一个例子，展示了我们通过这个结果实现的定位质量有多好。为了测试这一点，我们使用双目摄像头系统在某条特定的道路上行驶，并标记了一些不用于自我定位，而只是作为额外信息添加到地图中的3D结构。因此，我们恢复了一些结构的三维信息。如果你想看看都可以看到哪些结构，例如斑马线的边界或斑马线标志的柱子已经被使用并进行了映射，并确定了它们的三维位置。

在只使用单目摄像头的第二次行驶中，我们使用自我定位方法来确定车辆的位置，基于此，我们将地图中的3D结构投影到图像中。如果定位效果好，那么投影的3D结构应该与图像中看到的3D结构非常匹配；如果自我定位非常差，我们预计在图像中投影的结构与真实结构之间会存在较大差异。让我们来看一下。在这里，我们看到了那条道路，背景中有一些橙色的部分，这些是投影的对象。当然，在这里我们无法看到太多细节，也许你可以看到这些对象被投影到停车车辆上，这是事实，因为我们在这里没有进行任何遮挡分析，所以我们只是将这些结构投影到图像中，并显示它们确实是被投影的，而不是在图像中检测到的。现在我们靠近一点，这里可以明显看到我们将这些3D结构投影到图像中，而不是从图像中获取它们或者以某种方式在图像中标记它们。现在事情变得更有趣了，我们已经可以看到斑马线标志的柱子，它似乎很匹配。如果我们仔细看，也许会有一两个像素的偏差，但不超过这个范围。靠近一点，我们可以看到事物很好地吻合，再靠近一点，仍然很好地吻合。再重复一遍，这张图像中斑马线条纹的边界没有被标记，而是根据它们的3D位置进行投影到图像中。

我们可以看到它们非常匹配，这个隧道的其他结构也相当吻合。