模式识别
组合方法 Ensemble Methods
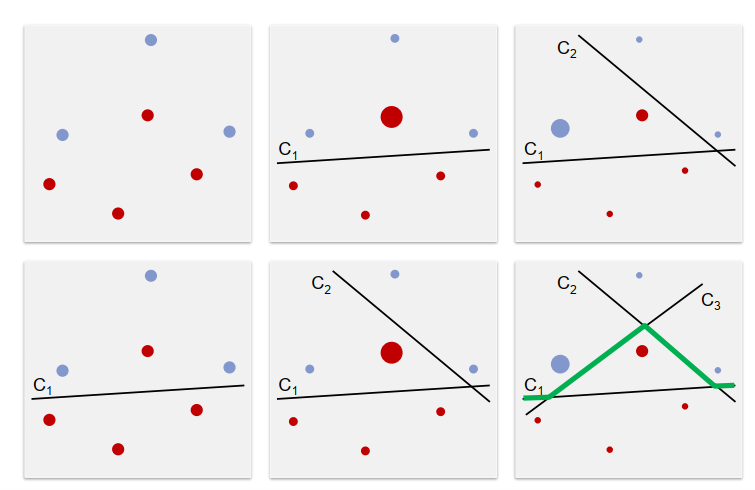
如果想解决分类问题,应该怎么做?
– 创建专家:训练分类器
– 训练几个分类器 → 并构建一个组合
集成学习归属于机器学习,他是一种「训练思路」,并不是某种具体的方法或者算法。
现实生活中,大家都知道「人多力量大」,「3 个臭皮匠顶个诸葛亮」。而集成学习的核心思路就是「人多力量大」,它并没有创造出新的算法,而是把已有的算法进行结合,从而得到更好的效果。
那组合怎么工作?
-
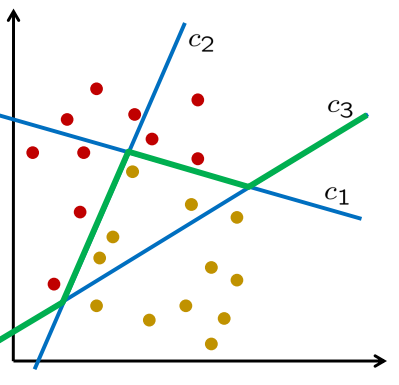
k分类器 $c_{1}, c_{2}, \ldots, c_{k}$
-
将相同的模式应用于所有分类器 → k 个预测
$\begin{array}{c}
c_{1}(\vec{x}) \in{-1,+1}
c_{2}(\vec{x}) \in{-1,+1}
c_{k}(\vec{x}) \in{-1,+1}
\end{array}$
- 总结所有预测并与零进行比较:
$\operatorname{ensemble}(\vec{x})=\operatorname{sign}\left(\sum_{j=1}^{k} c_{j}(\vec{x})\right)$
最好的四种数字识别方法:
- – (2) “线拟合”特征:99.7%
- – (3) 像素值:99.4%
- – (4) HOG 特征:99.7%
- – (5) Haar 特征:99.4%
- – (6) LBP 特征:99.3%
这些方法的组合会共享错误(在 1000 个测试示例中):
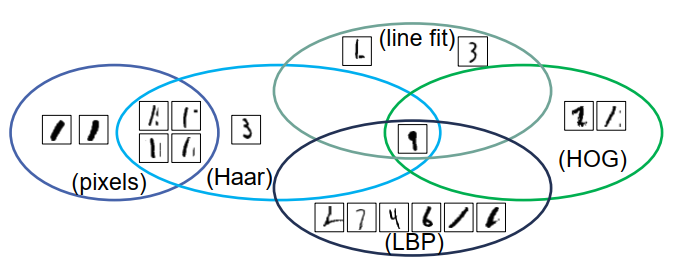
在实验数字识别中, 组合这些方法:
-
组合:线拟合、像素、Haar
错误率:5/1000 • 成员错误:3、6、6/1000
-
组合:线拟合、HOG、Haar
错误率:1/1000
成员错误:3、3、6/1000
具有联合特征的 SVM 错误:2/1000
-
组合:线拟合、HOG、LBP
错误率 1/1000
成员错误:3、3、7/1000
具有联合特征的 SVM 错误:5/1000
-
组合所有 错误率 1/1000
什么时候组合更有利?
最佳情况:分类器不共享错误
- 组合错误:0
- 每个分类器的错误:100
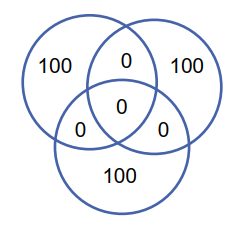
最差情况:分类器共享所有错误
- 组合错误:150
- 每个分类器的错误:100
所以关键问题就是:避免分类器共享错误
接下来引入:Boosting
-
训练相互依赖的分类器
-
第 n+1 号分类器 应该专注于被第 1...n号分类器 错误分类 的例子
Boosting
实现思路:
一、加权训练模式:为每个训练模式引入权重$\gamma_{i} \geq 0$以模拟其重要性
→ 有必要修改训练算法,例如soft margin SVM。
$\underset{\vec{w}, b}{\operatorname{minimise}} \frac{1}{2}|\vec{w}|^{2}+C \sum_{i}\left(\gamma_{i} \cdot \xi_{i}\right)$ subject to $d^{(i)} \cdot\left(\left\langle\vec{x}^{(i)}, \vec{w}\right\rangle+b\right) \geq 1-\xi_{i} \quad$ for all $i$ $\xi_{i} \geq 0 \quad$ for all $i$
如何确定模式权重? → 训练分类器后重新计算权重。
- 增加被错误分类的模式的权重
- 降低分类良好的模式的权重
实现思路:
二、 加权表决
为每个分类器引入权重$\beta_{k} \geq 0$以模拟其可靠性
→ 修改投票方案:
$\operatorname{ensemble}(\vec{x})=\operatorname{sign}\left(\sum_{k} \beta_{k} \cdot \text { vote }_{k}\right)$
如何确定投票权重?
→根据分类器的性能选择权重:
- 分类器权重大,准确率高
- 权重小,分类器准确率低
AdaBoost算法
Boosting是一种集合技术,试图从许多弱分类器中创建一个强分类器。这是通过从训练数据构建模型,然后创建第二个模型来尝试从第一个模型中纠正错误来完成的。添加模型直到完美预测训练集或添加最大数量的模型。
AdaBoost是第一个为二进制分类开发的真正成功的增强算法。这是理解助力的最佳起点。现代助推方法建立在AdaBoost上,最着名的是随机梯度增强机。
Adaboost是一种迭代算法,其核心思想是针对同一个训练集训练不同的分类器(弱分类器),然后把这些弱分类器集合起来,构成一个更强的最终分类器(强分类器)。
算法:

AdaBoost 的特性:
集成的训练误差由以下限制:
\[\prod_{t=1}^{T}\left(2 \sqrt{\epsilon_{t}\left(1-\epsilon_{t}\right)}\right) \leq \exp \left\{-2 \sum_{t=1}^{T}\left(\frac{1}{2}-\epsilon_{t}\right)^{2}\right\}\]如果 所有的$\epsilon_{t} \leq \lambda<\frac{1}{2}$ 和$T \rightarrow \infty$ AdaBoost 会产生一个完美的分类器
Haar分类器
概括来说:
Haar分类器=Haar-like特征+AdaBoost算法+级联+积分图快速计算
(1) Haar 特性
$s=\frac{1}{N_{\text {red }}} \sum_{(u, v) \in \text { red area }} g(u, v)-\frac{1}{N_{\text {blue }}} \sum_{(u, v) \in \text { blue area }} g(u, v)$
(2) 制作分类器
$c(s)=\operatorname{sign}(z \cdot(s-\theta))$
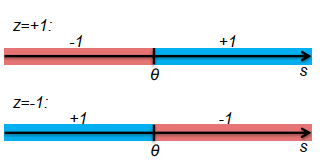
参数:
$\theta \in \mathbb{R}$ 阈值
$z \in{+1,-1}$ 方向
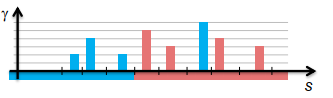
(3)从加权示例训练分类器:
-
尝试 θ 和 z 的所有可能值
-
选择最小化加权误差的值
$\sum_{s_{i}<\theta, d^{(i)}=z} \gamma_{i}+\sum_{s_{i}>\theta, d^{(i)}=-z} \gamma_{i}$
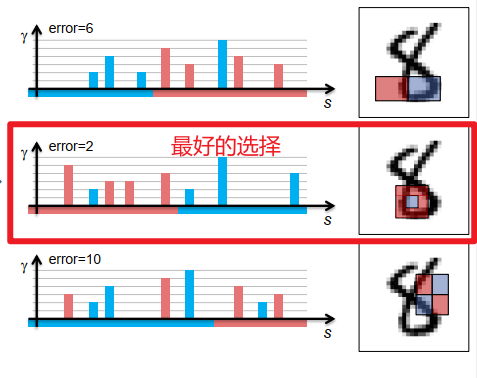
(4)具有多种功能的 Haar 分类器:
分类器在一组选项中选择一个 Haar 特征
Boosting 结合Haar分类器
Idea:
(1) 将 AdaBoost 与 Haar 分类器一起使用
数字识别任务的测试错误:
- 第一个分类器:56/1000
- 集合大小 5:54/1000
- 集合大小 50:16/1000
- 集合大小 200:10/1000
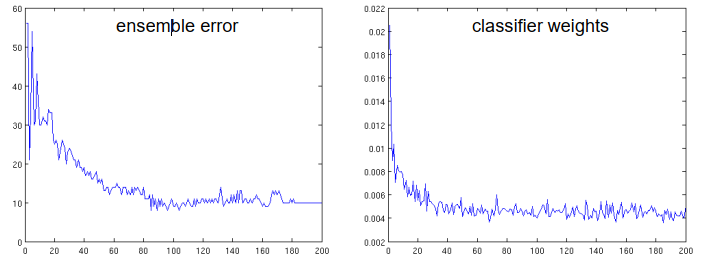
(2)每个特征产生一个分类器
例如 像素灰度
数字识别任务的测试错误:
- 第一个分类器:193/1000
- 集合大小 5:90/1000
- 集合大小 50:24/1000
- 集合大小 200:18/1000

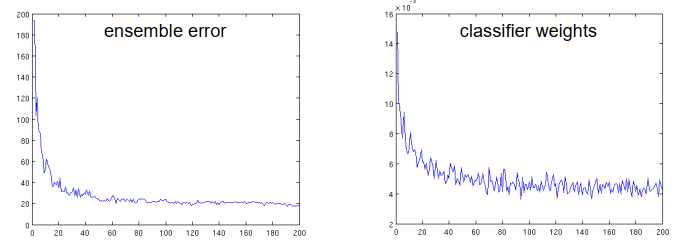
平衡错误
组合分类器:$\sum_{k}\left(\beta_{k} \cdot c_{k}(\vec{x})\right) \gtrless 0$
延伸:$\sum_{k}\left(\beta_{k} \cdot c_{k}(\vec{x})\right) \gtrless \delta$
δ > 0 :仅当非常确定时才分类为positive
δ < 0 :即使不确定,也可以将其归为positive
例子:
具有 Haar 功能的 AdaBoost,组合大小为5
$\sum_{k}\left(\beta_{k} \cdot c_{k}(\vec{x})\right) \gtrless \delta$
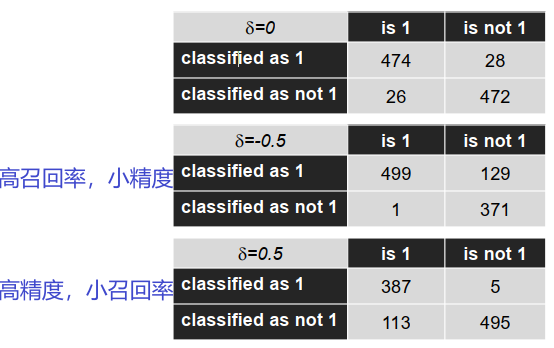
假设现在有这样一个测试集,测试集中的图片只由大雁和飞机两种图片组成. 假设你的分类系统最终的目的是:能取出测试集中所有飞机的图片,而不是大雁的图片,那么在这个任务中,飞机就是正例,大雁就是反例。
现在做如下的定义: True positives : 飞机的图片被正确的识别成了飞机。 True negatives: 大雁的图片没有被识别出来,系统正确地认为它们是大雁。 False positives: 大雁的图片被错误地识别成了飞机。 False negatives: 飞机的图片没有被识别出来,系统错误地认为它们是大雁。
Precision其实就是在识别出来的图片中,True positives所占的比率:
$precision = \frac{tp}{tp+fp} = \frac{tp}{n}$
其中的n代表的是(True positives + False positives),也就是系统一共识别出来多少照片 。
$recall = \frac{tp}{tp+fn}$
Recall 是被正确识别出来的飞机个数与测试集中所有飞机的个数的比值。
Recall的分母是(True positives + False negatives),这两个值的和,可以理解为一共有多少张飞机的照片。
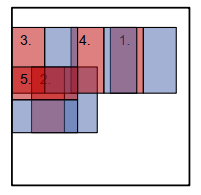
搜索对象 Searching for Objects
我们如何使用分类器在图像中找到对象?
– 例如 在字母上找到数字“1”;使用“1”的分类器


想法:
将分类器应用于所有图像中所有可能的区域
- 改变区域的位置
- 改变区域的大小
- 改变区域的方向(可选择)。 → 需要数百万次的试验 效率如何?
改进的想法:
使用两个分类器
分类器1
- 高效
- 不准确
- 高召回率
- 低精度
- 适用于所有领域
分类器2
- 低效率
- 精度
- 高召回率
- 高精度
- 适用于由分类器1发现的区域
想法可以扩展到一系列许多分类器 → Viola/Jones 算法
Viola/Jones Approach
结合:
– Haar 分类器
– AdaBoost
– 增加集合大小的分类器系列(“级联”)
– 调整集合以最大化召回率
– 搜索具有不同区域位置和大小的整个图像
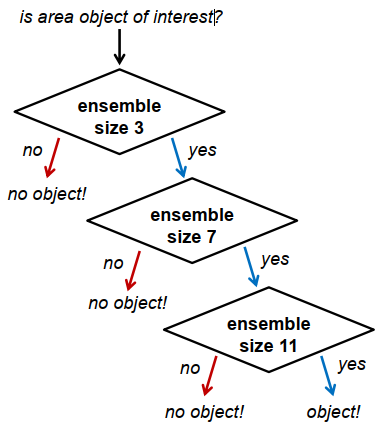
Viola/Jones算法举例
人脸识别
轮廓线检测
决策树:Decision Trees
决策树。
- 树状结构,分支因子2
- 内部节点:二进制分类器
- 叶子结点:类标签
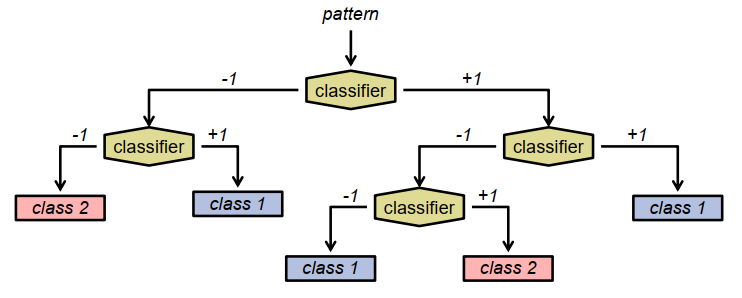
从训练示例创建决策树:
创建具有未知类标签的叶节点作为根节点。
将所有训练示例分配给它.

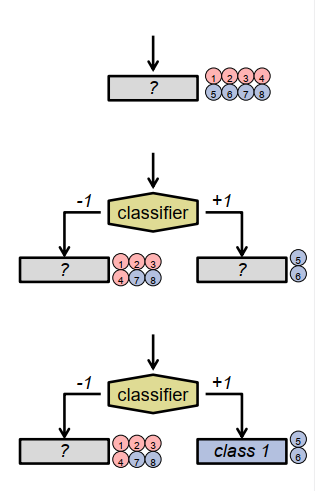
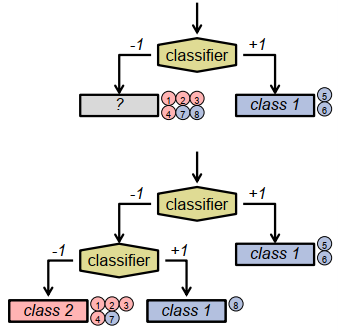
哪些分类器是合适的?
– 一般来说:全部
– 类似的想法,例如 boosting:
通过组合简单分类器创建一个复杂分类器,即阈值分类器: 如使用 Haar 分类器进行数字识别
数字识别决策树:
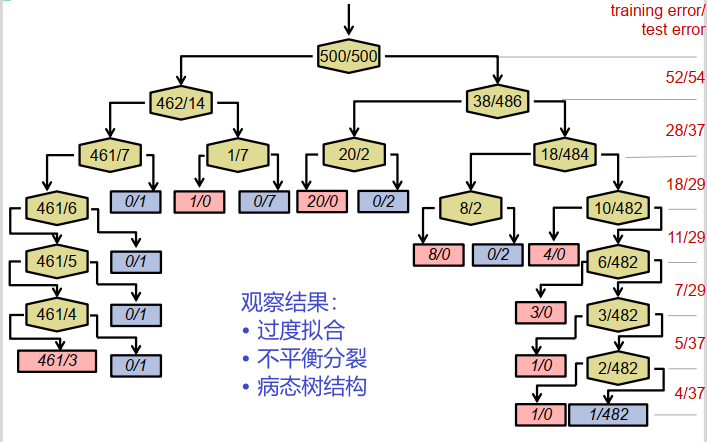
改进决策树的技术
正则化技术Regularization techniques:
机器学习中的一个核心问题是设计不仅在训练集上误差小,而且在新样本上泛化能力好的算法。许多机器学习算法都需要采取相应的策略来减少测试误差,这些策略被统称为正则化。
1. 早期止损 在构建树时使用验证集。当你在验证集上观察到非递减的错误时,停止分割节点。 你观察到验证集上的错误没有减少。
- 例如:数字识别的验证误差是。 深度为1的树为54 深度为2的树为37 深度3的树为29 深度4的树为29 深度5的树为29 深度为7的树为36 深度为7的树为37 → 取深度为3的树
2.修剪
首先创建完整的决策树。 之后去除不平衡或病态的分支。
• 几个修剪标准
• 已经应用过,例如 在决策树算法 C4.5
3.随机决策树和森林
通过以下方式随机创建决策树:
- 随机选择训练数据的子集
- 随机选择作为下一次拆分选项的特征子集
- 随机选择区分阈值
构建许多随机树的集合:
→ 随机决策森林
创建决策森林
– 使用 Haar 特征
– 随机选择特征和阈值(在 k 个试验中最好)
– 训练集没有变化
– 允许深度树
– 改变集合大小 n
测试集错误:
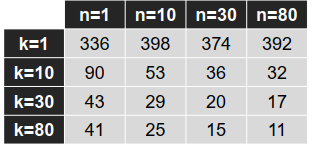
比较:
-
使用早期停止训练的决策树:29
-
AdaBoost 集成
-
大小 5:54
-
大小 50:16
-
大小 200:10
-
-
SVM:6
结合多类别分类器的决策树
扩展到两个以上的类:
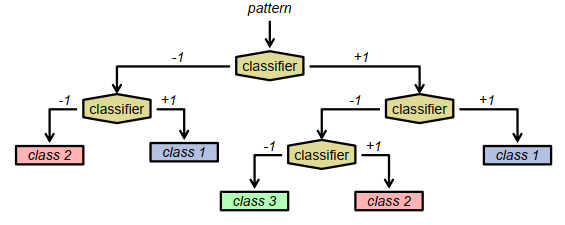
训练分类器以最小化叶节点中的香农熵
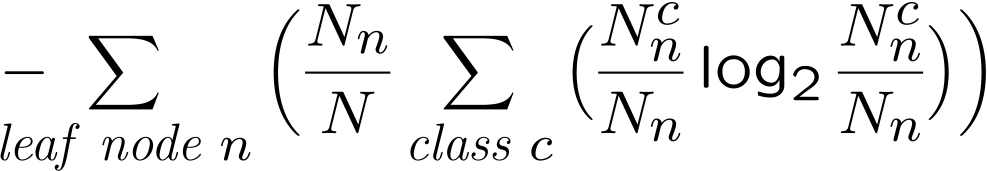

熵衡量模式集的同质性
- 所有模式属于同一类:熵最小 (0)
- 相同数量的模式属于每个类:熵最大