模式识别 Pattern Recognition

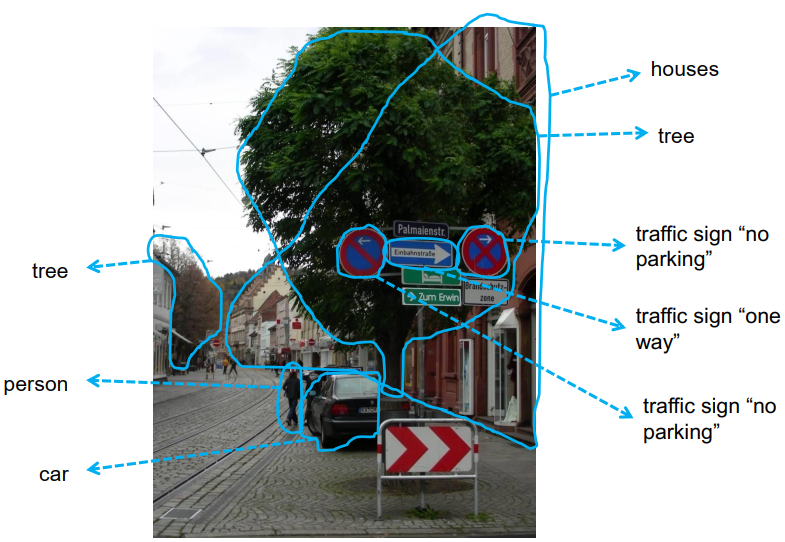
分类：将对象分配到类别（classes）。

维基百科：

模式识别，就是通过计算机用数学技术方法来研究模式的自动处理和判读。我们把环境和客体统称为“模式”。随着计算机技术的发展，人类有可能研究复杂的信息处理过程。

信息处理过程的一个重要形式是生命体对环境及客体的识别。

以光学字元识别之“汉字识别”为例：首先将汉字图像进行处理，抽取主要表达特征并将特征与汉字的代码存在计算机中。就像老师教我们“这个字叫什么、如何写”记在大脑中。这一过程叫做“训练”。识别过程就是将输入的汉字图像经处理后与计算机中的所有字进行比较，找出最相近的字就是识别结果。这一过程叫做“匹配”。

我们如何区分物体？

• 几何特征，如长宽比、圆度，……。
• 颜色特征，如主要色调、平均 饱和度，颜色的差异性，…

从实例中学习

• 收集物体的图像
• 为每个物体创建一个特征向量（”模式”）。
• 找到一个决策规则来区分不同类别的特征向量之间的类别
• 从实例模式中创建一个决策规则的过程，决策规则的过程被称为 “学习”或 “训练”

许多方法用于决策规则和学习

• 线性分类器
• 人工神经网络/深度学习
• 基于原型的方法
• 基于案例的推理
• 决策树
• 支持向量机
• boosting算法

本次我们讨论： 线性分类器，支持向量机，boosting，决策树，深度学习

线性分类器：Linear Classification

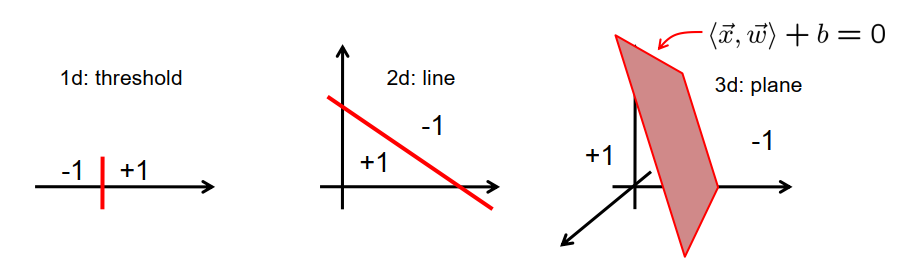
线性分类器是以下类型的函数：

$\vec{x} \mapsto \begin{cases}+1 & \text { if }\langle\vec{x}, \vec{w}\rangle+b \geq 0 \ -1 & \text { otherwise }\end{cases}$

$\vec{w}$是线性分类器的权向量

$b$是分类器的偏置权重

线性分类器将输入空间细分为两个半空间。 决策边界是一个超平面

学习任务：

给定一组训练样例：

$d^{(i)}=+1$属于一类的例子（“positive examples”）

$d^{(i)}=-1$对于属于另一类的示例（“negative examples”）

寻找 $\vec{w}$和 使其：

$d^{(i)} \cdot\left(\left\langle\vec{x}^{(i)}, \vec{w}\right\rangle+b\right)>0 \quad$ for all $i \in{1, \ldots, p}$$

许多可能的解决方案，哪一个是最好的？

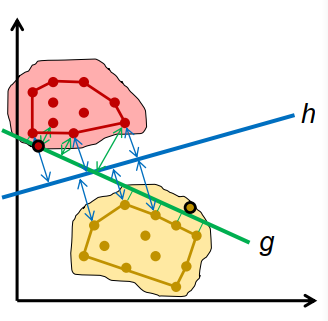
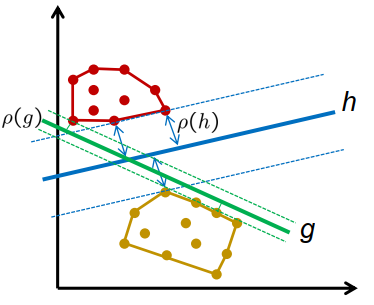
• g 和 h，两者都不会产生分类错误
• g 与模式的距离比 h 短
• g 新模式的错误分类风险大于 h
• （未知）类概率分布的支持类似于凸包 训练示例

边距：超平面和训练模式的凸包之间的最小距离

$\rho=\min _{i}\left(d^{(i)} \cdot \frac{\left\langle\vec{x}^{(i)}, \vec{w}\right\rangle+b}{|\vec{w}|}\right)$

支持向量机 SVM

支持向量机 (SVM) ：support vector machine (SVM) ： 最大化边距的线性分类器

支持向量机 (SVM)——训练 SVM 意味着解决：

$\begin{array}{ll}\underset{\rho, \vec{w}, b}{\operatorname{maximise}} & \rho^{2} \ \text { subject to } & d^{(i)} \cdot \frac{\left\langle\vec{x}^{(i)}, \vec{w}\right\rangle+b}{|\vec{w}|} \geq \rho \quad \text { for all } i \ & \rho>0\end{array}$

一个自由度：$|\vec{w}|$

简化：

$|\vec{w}|=\frac{1}{\rho}$

$\underset{\vec{w}, b}{\operatorname{minimise}} \frac{1}{2}|\vec{w}|^{2}$ subject to $d^{(i)} \cdot\left(\left\langle\vec{x}^{(i)}, \vec{w}\right\rangle+b\right) \geq 1 \quad$ for all $i$

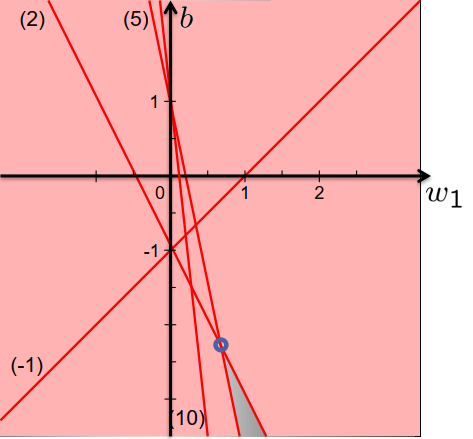
一个简单的例子：

模式是一维的：

正的：5，10；

负的：-1，2

参数：$\vec{w_1},b$

最优化问题：

$\underset{w_{1}, b}{\operatorname{minimise}} \frac{1}{2} w_{1}^{2}$

使其：

$b \geq 1-5 w_{1}$ $b \geq 1-10 w_{1}$ $b \leq-1+w_{1}$ $b \leq-1-2 w_{1}$

但是如何训练一个SVM呢？

$\operatorname{minimise}_{\vec{w}, b} \frac{1}{2}|\vec{w}|^{2}$ 使其 $d^{(i)} \cdot\left(\left\langle\vec{x}^{(i)}, \vec{w}\right\rangle+b\right) \geq 1 \quad$ for all $i$

…跳过所有细节…

– 应用拉格朗日乘数理论

– 每个训练模式一个拉格朗日乘数

– 解决方案完全由拉格朗日乘数描述

– 许多拉格朗日乘数为零

– 存在计算拉格朗日乘数的算法

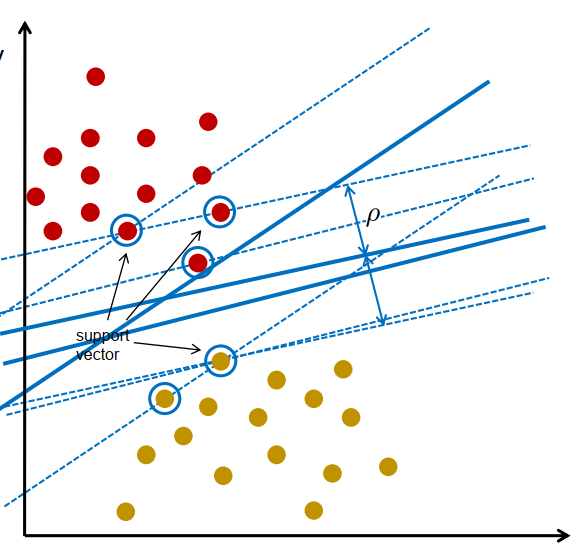
解决方案：

• 由支持向量确定的最优分离超平面

• 移除非支持向量不会改变解

• 添加距离大于边距的模式不会改变解

• 移除支持向量会改变解

• 添加距离小于边距的模式会改变解

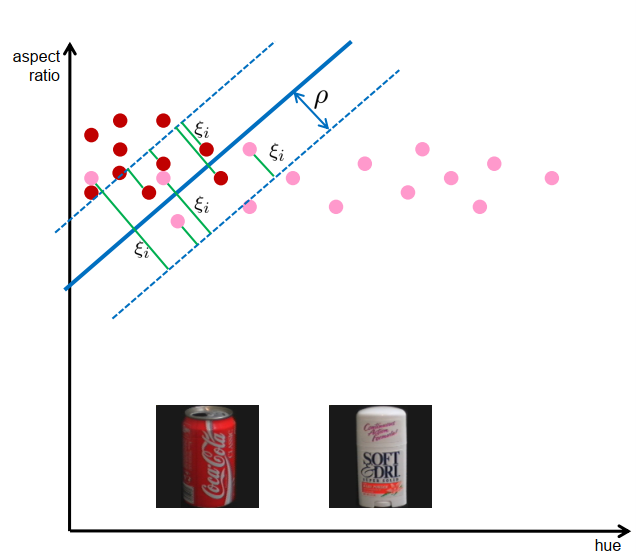
容错SVM Fault-tolerant SVMs

• 重叠的类迫使制造错误

人为错误$\xi_{i}$

冲突的目标：

使 $\rho$最大化，使$\xi_{i}$ 最小化

最优化问题：

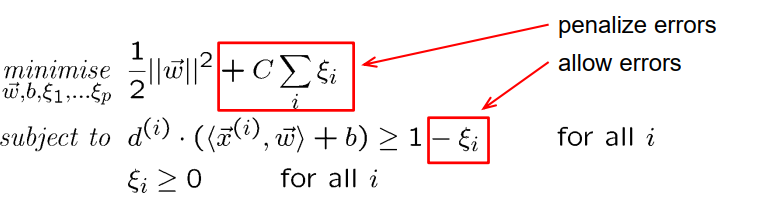
C>0：正则化参数控制小误差和大余量之间的平衡（必须手动选择）

容错 SVM 被称为“soft-margin-SVMs”（与“hard-margin-SVMs”相反）

hard-margin-SVMs有类似的解决方案

支持向量是产生单个错误或位于边缘区域边界上的所有模式

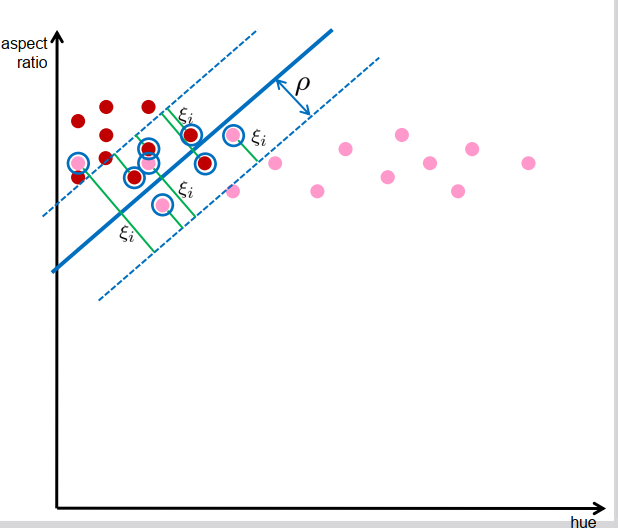
非线性SVM Nonlinear SVMs

具有非重叠支持的类可能不是线性可分的 → 非线性分类器

• 直接方式：使用圆形/椭圆/非线性曲线进行分类 → 难以分析

• 间接方式：非线性变换数据并改为对变换后的数据进行分类

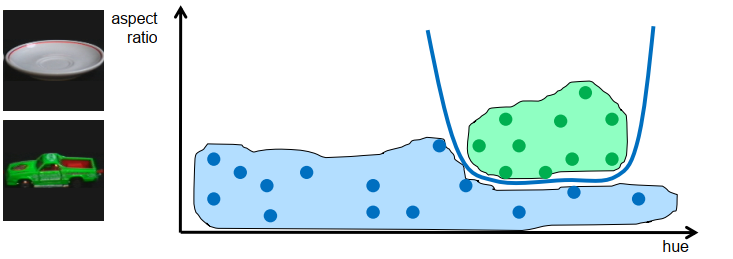
非线性问题可能在非线性变换后变为线性问题

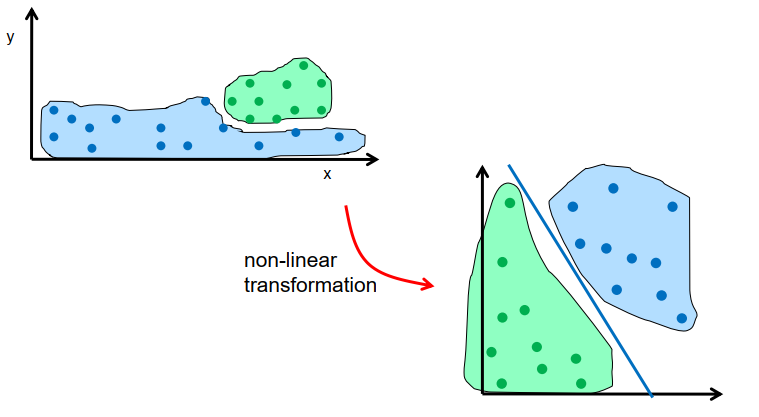
假设非线性变换

找到解决问题的 SVM：

$\underset{\vec{W}, b}{\operatorname{minimise}} \frac{1}{2}|\vec{W}|^{2}$ subject to $d^{(i)} \cdot\left(\left\langle\vec{X}^{(i)}, \vec{W}\right\rangle+b\right) \geq 1 \quad$ for all $i$

在知道拉格朗日乘数的情况下，解决方案完全确定：

– 不需要计算

– 模式仅作为点积的参数成对出现

考虑到：$\left\langle\Phi\left(\vec{x}^{(i)}\right), \Phi\left(\vec{x}^{(j)}\right)\right\rangle$

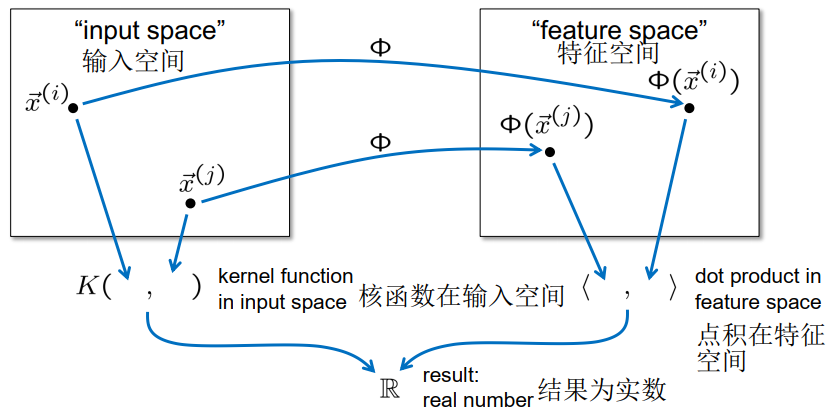
快捷方式：核函数$K(\vec{x}, \vec{y})=\langle\Phi(\vec{x}), \Phi(\vec{y})\rangle$

通过$\phi$ 消除$K(\vec{x}, \vec{y})$ 来代替$\langle\Phi(\vec{x}), \Phi(\vec{y})\rangle$

核函数是隐藏复杂性的肮脏技巧吗？

例如：$\Phi(x)=\left(\begin{array}{c}x^{2} \ x\end{array}\right)$

•评估 Φ(x) 和 Φ(y) 需要 2 次乘法

•评估特征空间中的点积需要 2 次乘法和 1 次加法，总共：4 次乘法和 1 次加法

$K(x, y)=\langle\Phi(x), \Phi(y)\rangle=(x y)^{2}+(x y)$

•评估核函数需要 2 次乘法和 1 次加法

一些内核基于无限维的希尔伯特空间

一些有用的核函数：

• 点积：$K(\vec{x}, \vec{y})=\langle\vec{x}, \vec{y}\rangle$
• 多项式核函数：$K(\vec{x}, \vec{y})=(\langle\vec{x}, \vec{y}\rangle)^{q}$ or $(\langle\vec{x}, \vec{y}\rangle+1)^{q}$
• 径向基函数 (RBF) 内核 $K(\vec{x}, \vec{y})=e^{-\frac{|\vec{x}-\vec{y}|^{2}}{2 \sigma^{2}}}$
• 直方图交叉核（仅适用于直方图特征）

内核参数必须手动设置

现在结合所有想法：

• 支持向量机最大化边距以最小化错误分类的风险
• 软边距支持向量机允许个别错误。 由参数 C 控制边距大小和误差之间的平衡
• 核函数允许在不改变理论框架的情况下进行非线性分类。 内核类型和内核参数控制非线性程度

使用SVMs

1. 应用SVM：

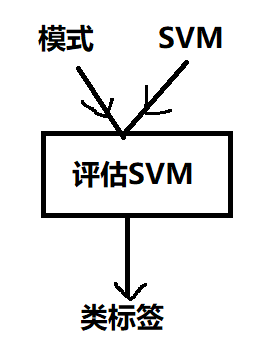
1. 训练SVM：

   我们如何确定 C 和内核？

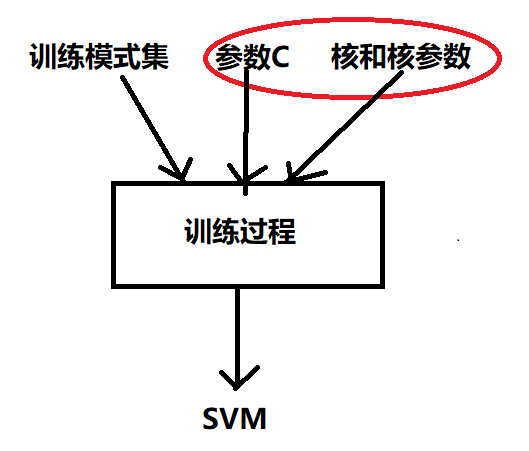
评估SVM

错误分类的风险 = “false negative”的风险 + “false positive ”的风险

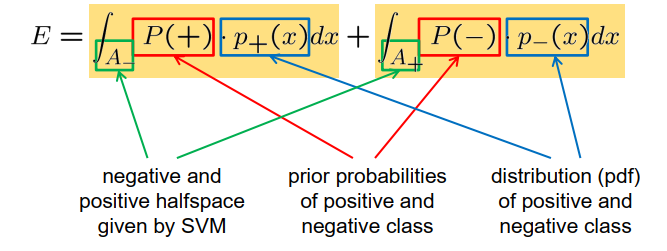
E 未知，但可以从样本集中近似

$E \approx \frac{n_{f n}+n_{f p}}{n}$

– 样本集中的元素数量

– 样本集中的假阳误报数量

– 样本集中的假阴误报数量

• 验证是在样本集（“测试集”、“验证集”）上测试分类器性能的过程

• 选择测试集上误分类率最小的 SVM

• 测试集必须独立于训练集！

• 验证允许比较使用不同 C 值和不同内核训练的 SVM 的性能

交叉验证 Cross Validation

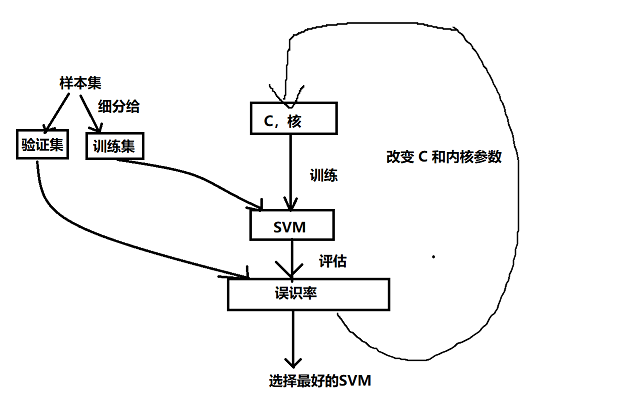
• 验证过程的缺点：

– 仅部分数据用于训练

– 仅部分数据用于验证

• k -fold 交叉验证

– 想法：用不同的训练和验证集重复训练/验证过程几次

–  k 是重复次数（介于 2 和模式数之间）

K-fold交叉验证法

1. 将模式集细分为K个大小相同的不相干子集
2. 对每个子集j重复。 2.1 从子集1,…,j-1,j+1,…k训练SVM 2.2. 评估子集j的错误分类率
3. 平均错误分类率

优点：

– 所有模式都用于验证

– 训练集包含一定比例$\frac{k-1}{k}$的模式

如果 k 等于模式总数 → leave-one-out-error

例子 3-fold-cross-validation ：

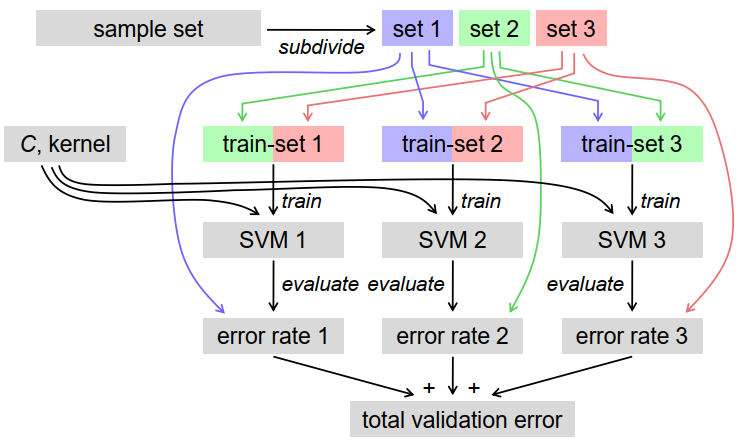
在参数空间中搜索最优参数的可能性，例如

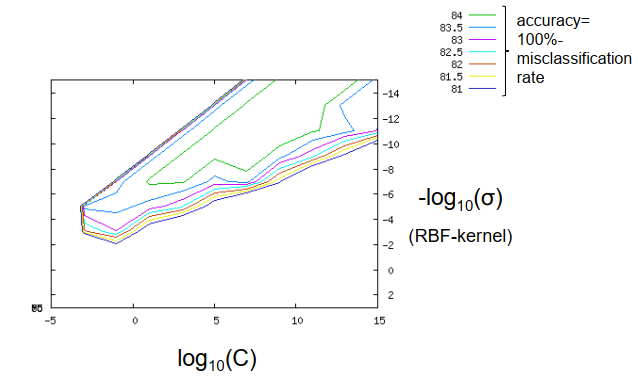
应该听说过的一些概念：

• 过度拟合：分类器在训练数据上表现良好，但在验证或测试数据上表现不佳
• 欠拟合：分类器在训练和验证数据上表现不佳
• 泛化：从训练示例中学习一个概念 也适用于测试数据，而不仅仅是记住训练示例
• 正则化：“帮助”过度拟合的分类器来提高泛化能力

实验： 数字识别

对手写数字的图像进行分类（美国邮政编码）

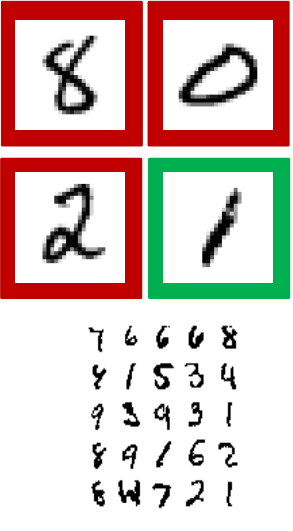
简化任务：分类——图像显示数字“1”——图像不显示数字“1”

在这里：

– 用于训练和验证：500 个“1”图像，500 个“no-1”图像

– 用于测试：500 个“1”图像，500 个“not-1”数据集图像

第一种方法 2-dimensional patterns

– 二维模式

• 平均灰度值
• 纵横比

– 模式重新调整为区间 [-1, +1]

– 带 RBF 内核的软边距 SVM

– 5-fold交叉验证

– 参数空间中的网格搜索：

$10^{-5} \leq C \leq 10^{15}$(on log scale)

$- 10^{-3} \leq \sigma \leq 10^{15} $(on log scale)

准确率： − 交叉验证：93.1% − 测试集：80.3%

支持向量数：167（共 1000 个）

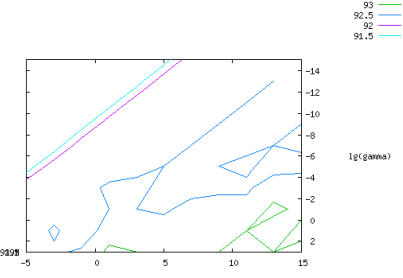
第二种方法 添加第三个特征

– 添加第三个特征：拟合线到暗像素的平均距离

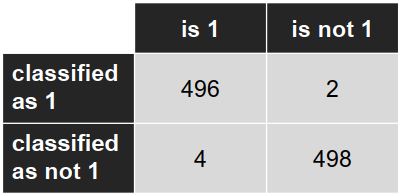
– 准确度： - 交叉验证：98.5% - 测试集：98.7%

支持向量的数量：95（共 1000 个）

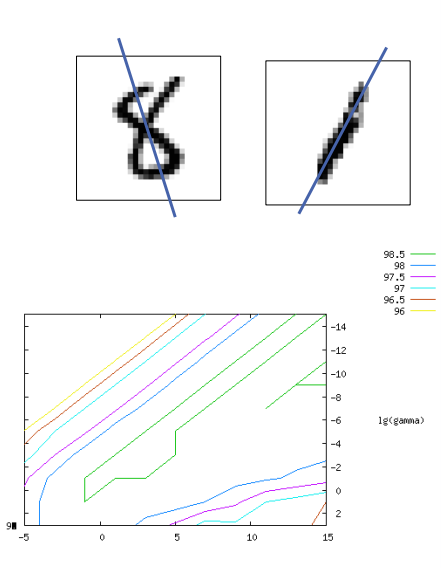
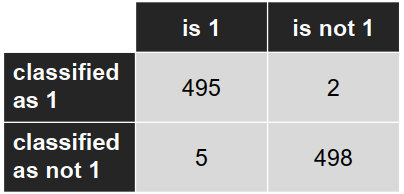
混淆矩阵: (Confusion matrix)

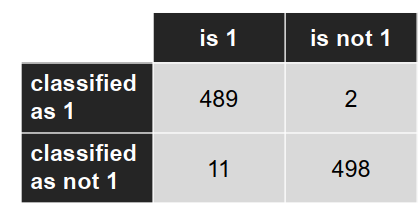
第二种方法改进 找到连通分量 (CCL) 并屏蔽除最大段以外的所有部分

– 找到连通分量 (CCL) 并屏蔽除最大段以外的所有部分

– 从预处理图像计算特征

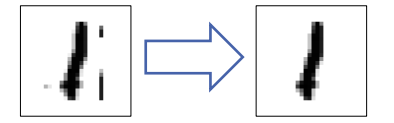
准确率： − 交叉验证：98.5% − 测试集：99.7%

支持向量数：95（共 1000 个）

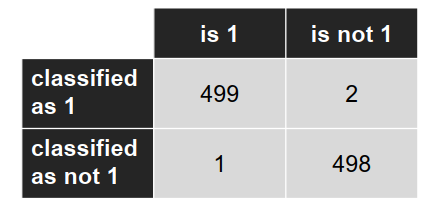
第三种方法 统一缩放图片

– 将所有图像的大小调整为 28x28 像素，并使用像素的灰度值作为特征

→ 784-维模式

准确率：- 交叉验证：99.0% - 测试集：98.7%

支持向量数量：220（1000 个）

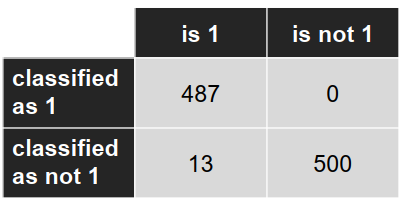
第三种方法改进 只使用一部分像素

• 观察：很多像素不影响分类，例如 边界像素

• 仅使用所有像素的子集，例如 24x18 子区域 → 432 维图案

  

准确度：- 交叉验证：99.0% - 测试集：99.4%

支持向量数：219（共 1000 个）

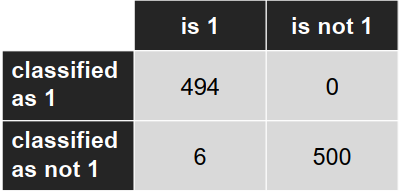
第四种方法 HOG-features

HOG-features

– 定向梯度直方图 (Dalal&Triggs, 2005)

使用梯度信息而不是灰度级

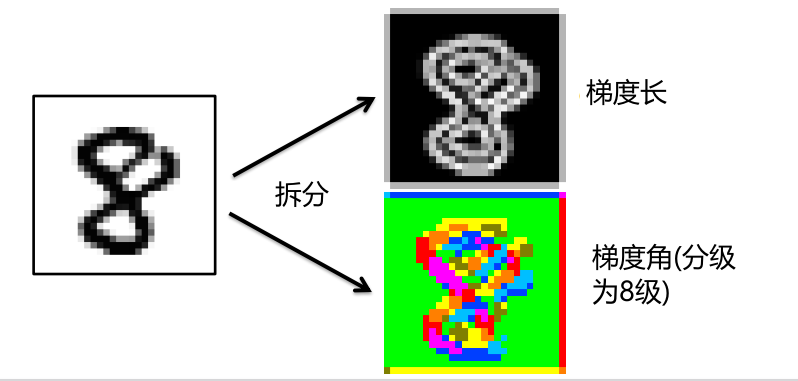
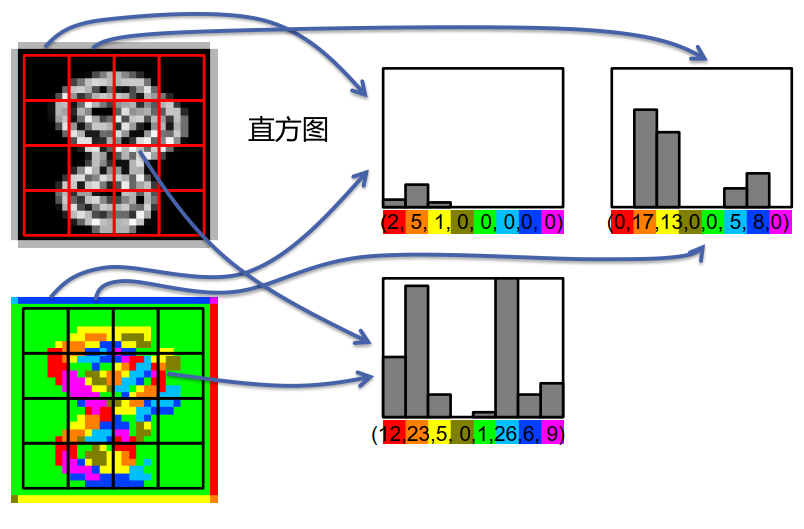
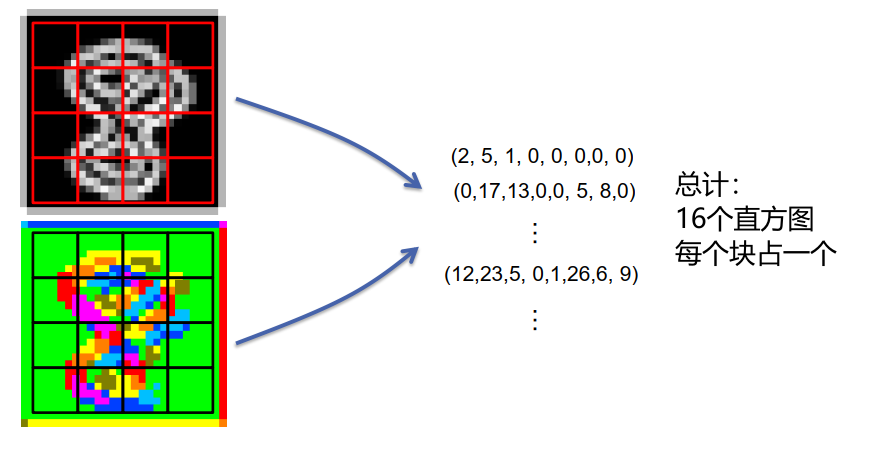
HOG 排列 4 个相邻单元的归一化块:

规范化描述符：

组装所有块的描述符：

将向量$\vec{V}$应用于 SVM

第四种方法： – 仅使用 HOG 特征 → 288 维模式

准确率： − 交叉验证：99.4% − 测试集：99.7%

支持向量的数量：174（共 1000 个）

第五种方法 哈尔特征 Haar features

哈尔特征（Haar features）

哈尔特征使用检测窗口中指定位置的相邻矩形，计算每一个矩形的像素和并取其差值。然后用这些差值来对图像的子区域进行分类。

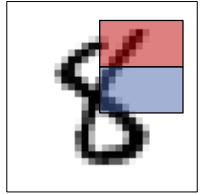
比较矩形区域的灰度，即红色区域的平均灰度减去蓝色区域的平均灰度。

Haar特征在一定程度上反应了图像灰度的局部变化。

在人脸检测中，脸部的一些特征可由矩形特征简单刻画，例如，眼睛比周围区域的颜色要深，鼻梁比两侧颜色要浅等。

有很多可能的特征

边缘特征：

线特征：

棋盘特征：

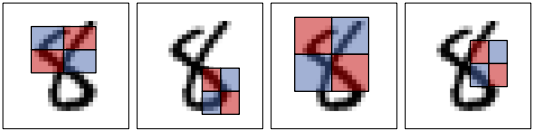
中心环绕特征

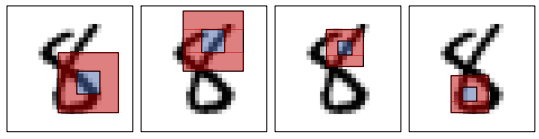
对角线方向的特征

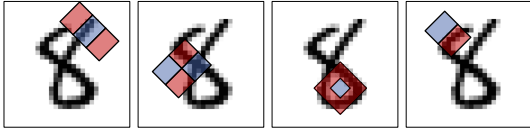
1. 计算哈尔特征：

1. 简单的直接操作：

$s=\sum_{u=u_{0}}^{u_{0}+w-1} \sum_{v=v_{0}}^{v_{0}+h-1} g(u, v)$

用 for 循环实现这一点需要操作

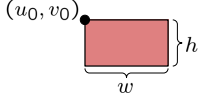
1. 比较好用的方式

$s=\sum_{u=0}^{u_{0}+w-1} \sum_{v=0}^{v_{0}+h-1} g(u, v)-\sum_{u=0}^{u_{0}-1} \sum_{v=0}^{v_{0}+h-1} g(u, v)+\sum_{u=0}^{u_{0}-1} \sum_{v=0}^{v_{0}-1} g(u, v)-\sum_{u=0}^{u_{0}+w-1} \sum_{v=0}^{v_{0}-1} g(u, v)$

积分图像：

$I(x, y):=\sum_{u=0}^{x} \sum_{v=0}^{y} g(u, v)$

计算 s 需要 4 个操作：

$\begin{array}{c} s=I\left(u_{0}+w-1, v_{0}+h-1\right)-I\left(u_{0}-1, v_{0}+h-1\right)+
I\left(u_{0}-1, v_{0}-1\right)-I\left(u_{0}+w-1, v_{0}-1\right) \end{array}$

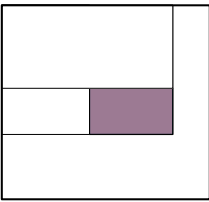
2. 计算积分图像

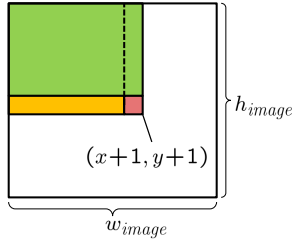
$I(x, y):=\sum_{u=0}^{x} \sum_{v=0}^{y} g(u, v)$

$\begin{aligned} I(x+1, y+1) &=\sum_{u=0}^{x+1} \sum_{v=0}^{y+1} g(u, v)
&=\sum_{u=0}^{x+1} \sum_{v=0}^{y} g(u, v)+\sum_{u=0}^{x} \sum_{v=0}^{y+1} g(u, v)-\sum_{u=0}^{x} \sum_{v=0}^{y} g(u, v)+g(x+1, y+1)
&=I(x+1, y)+I(x, y+1)-I(x, y)+g(x+1, y+1) \end{aligned}$

–> 产生一个迭代算法，通过操作计算$O\left(w_{\text {image }} \cdot h_{\text {image }}\right)$整个积分图像

–>如果想计算一个矩形，简单的方法更好；如果要计算许多矩形，积分图像会更好

Haar 特征，在 7x7 位置使用水平和垂直边缘特征 → 98 维模式

准确率： − 交叉验证：99.1% − 测试集：99.4%

支持向量数：109（共 1000 个）

第六种方法：

局部二值模式 [Local binary patterns (LBP) ]

• 分析局部灰度变化
• 对多个区域执行直方图

1. 对于每个相邻像素，检查相邻像素是更亮 (1) 还是更暗 (0)

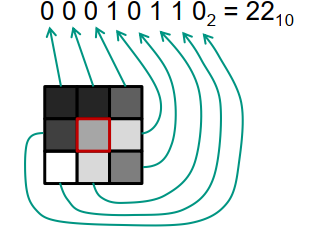
1. 计算块中所有像素的这些数字

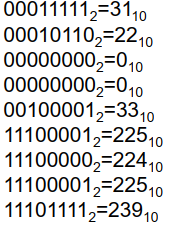
1. 制作直方图
2. 将所有块的直方图排列在一个向量中

局部二进制模式 → 4096 维稀疏模式

准确度：- 交叉验证：98.6% - 测试集：99.3%

支持向量的数量：264（共 1000 个）

总结

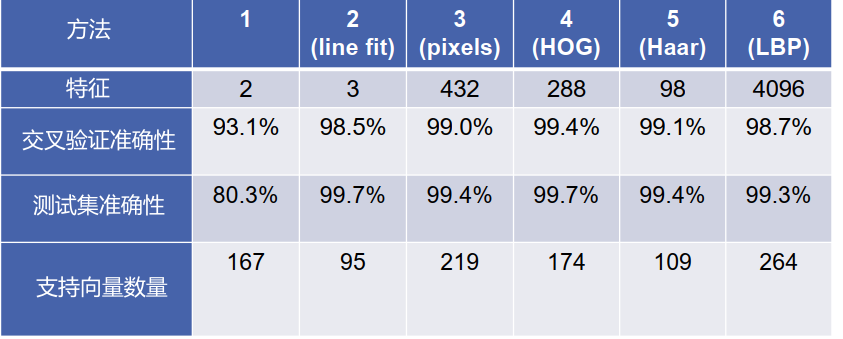
见解：

– 训练和测试的准确度不一样

– “智能”特性有很大帮助

– 更多的功能并不意味着更高的准确度

– “智能”特性包括预处理

– “通用”特征（像素值、HOG、Haar）

图像数据增强Data Tuning

训练数据的质量和数量对分类结果的影响很大

(一) 我们如何提高数量？

• – 选择和标记更多图像
• – 搜索数据库/互联网以获取更多训练示例（ImageNet、KITTI、CalTech 数据集、INRIA 数据集、Microsoft COCO，…）
• – 改变亮度、对比度、ROI 中对象位置、旋转的示例
• – 添加抖动（ 随机噪声）
• – 镜像示例，如果对象是对称的
• – 弹性变形 Elastic Distortion

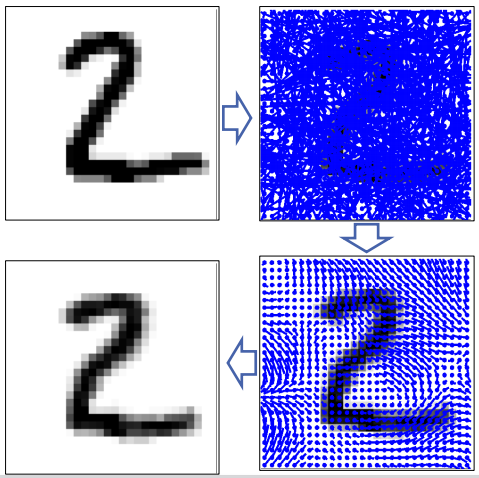
弹性变形

1. 对于每个像素：样本从高斯分布随机偏移
2. 通过与高斯滤波器的卷积平滑移位值
3. 对于每个像素：将像素移动到新位置

（二）我们如何提高质量？

• – 检查标签的一致性
• – 标准化/标准化模式
• – 从各种来源/具有不同条件的各种图像序列中获取数据 → 增加模式集中的变化
• – 检查 ROI 是否一致

$\begin{array}{l} x_{i}^{\prime}=\frac{x_{i}-\bar{x}}{s_{x}}
\text { with } \bar{x}=\frac{1}{n} \sum_{i} x_{i}
\text { and } s_{x}=\sqrt{\frac{1}{n} \sum_{i}\left(x_{i}-\bar{x}\right)^{2}} \end{array}$

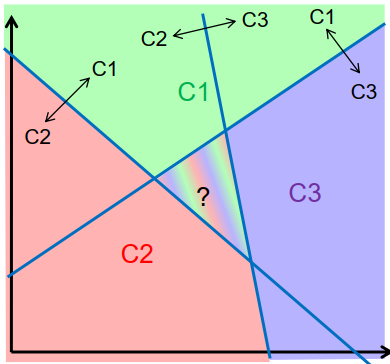
多种类分类

具有两个以上类别的分类

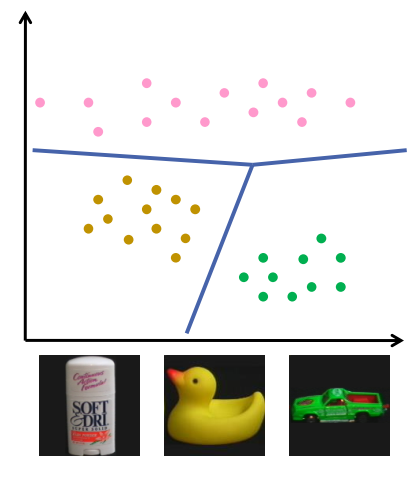
一对一的方法：

为每个类构建一个分类器，对类元素与非类元素进行分类

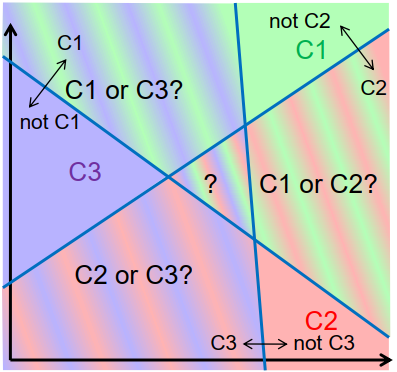
克服歧义：