形态学运算 Morphological Operations
对于图像具有的问题:孔洞, 参差不齐的轮廓,间隙,微小区域等,我们提出了形态学运算。
两个关键概念:扩展和缩小区域:
——腐蚀erosion: 将区域缩小一个像素
——膨胀dilation:将区域扩大一个像素
最基本的形态学运算是膨胀和腐蚀。膨胀指将像素添加到图像中对象的边界,而腐蚀指删除对象边界上的像素。
现在我们假设:
背景的像素用0编码,前景像素用大于1的数字编码。
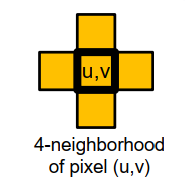
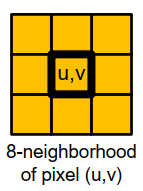

腐蚀:
\[\begin{aligned} \operatorname{erode}\{g\}(u, v)=\min \{& g(u, v) \\ & g(u+1, v), g(u+1, v+1) \\ & g(u, v+1), g(u-1, v+1) \\ & g(u-1, v), g(u-1, v-1) \\ &g(u, v-1), g(u+1, v-1)\} \end{aligned}\]取相邻的最小值
膨胀:
\[\begin{aligned} \operatorname{dilate}\{g\}(u, v)=\max &\{g(u, v)\\ & g(u+1, v), g(u+1, v+1), \\ & g(u, v+1), g(u-1, v+1) \\ & g(u-1, v), g(u-1, v-1) \\ &g(u, v-1), g(u+1, v-1)\} \end{aligned}\]取相邻的最大值
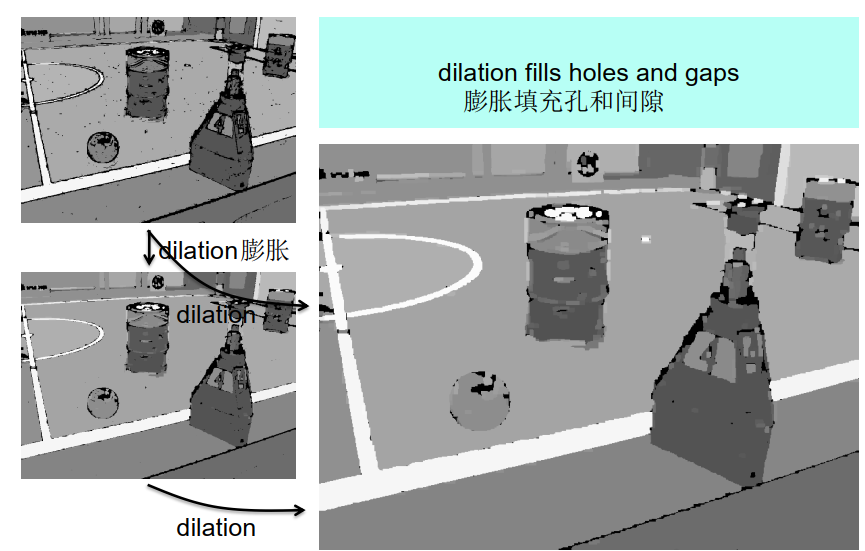

然后一个巧妙地知识:腐蚀和膨胀能够结合
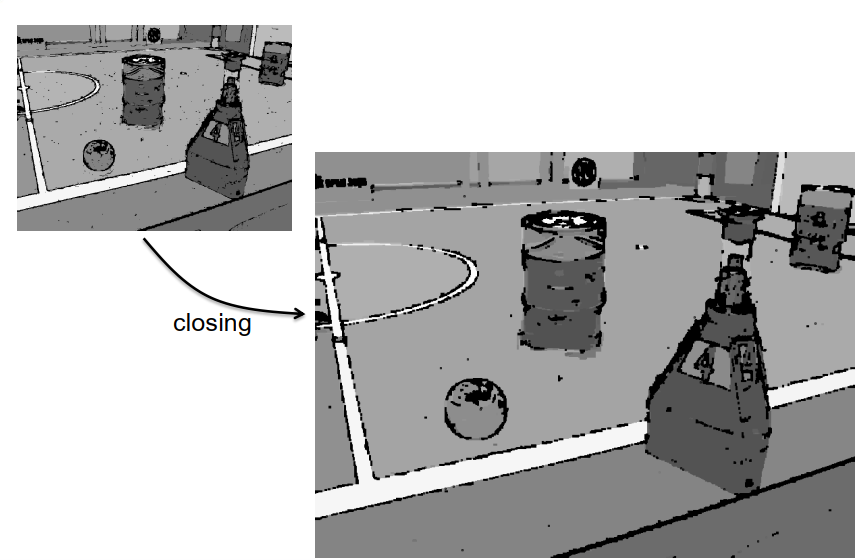
—— 闭合colsing:先膨胀,再腐蚀
在不改变区域整体延伸的情况下填充间隙和孔洞
—— 开放opening:先腐蚀,再膨胀
去除薄区域而不改变大区域的整体延伸

到目前为止,我们的分割是:
——分割基于颜色(或灰度值)
——不同的颜色表示和不同的相似度测量
问题是:我们如何分割颜色不显著的图像
例如:将图像分割成相同阴影的区域
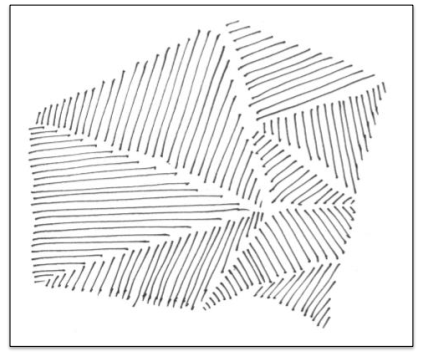
那我们分割图像又需要什么呢?
对每个像素:对该像素的描述(图像特征)。
- 如:颜色
- 如:纹理信息
- 如:点的深度(三维扫描仪/立体视觉)
- 如:像素的运动(光流)。
- 如:描述像素是否属于某些物体类别的特征
- 再例如,这些特征的组合
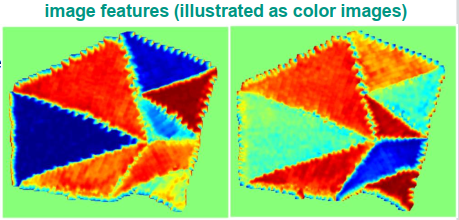
在上述例子中,我们又将找到了什么样子的图像特征呢:
图像特征:
- 颜色和灰度等级不突出
- 线条的方向是突出的
- 例如
- 计算灰度等级的梯度
- 确定主要的梯度方向 在像素周围的局部环境中
- 用2维矢量表示方向
- 矢量的长度与平均梯度长度成正比 梯度长度
我们的准则和算法:
• 邻域标准
• 最小分段大小
• CCL
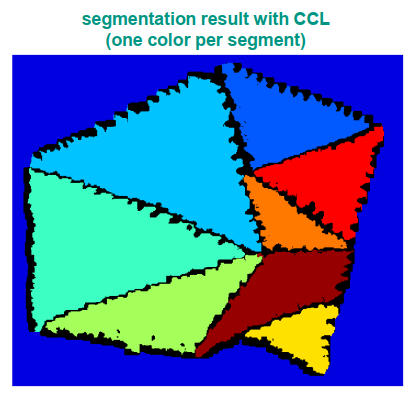
水平集方法 Let Set Methods
这个方法我的个人理解是通过一段任意封闭的曲线进行扩张,当扩张到图像梯度明显的地方开始放缓扩张速度直到停止,从而形成一段对具有对明显图像特征的区域进行包络。



二类图像分割:
表示分类任务中有两个类别,比如我们想识别一幅图片是不是猫。也就是说,训练一个分类器,输入一幅图片,用特征向量x表示,输出是不是猫,用y=0或1表示。二类分类是假设每个样本都被设置了一个且仅有一个标签 0 或者 1。
这类分割的特点:
所有像素的集合都属于分割;
指示函数indicator function:
\[\phi(\vec{x}) \begin{cases}<0 & \text { if pixel } \vec{x} \text { belongs to segment } \\ >0 & \text { if pixel } \vec{x} \text { belongs to background }\end{cases}\]边界线
有符号距离函数
\[|\phi(\vec{x})|= \text{ distance of } \vec{x} \text{ from contour}\]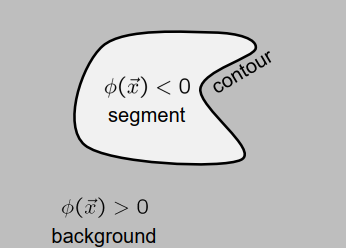
轮廓点:
\[\phi(\vec{x})= 0\]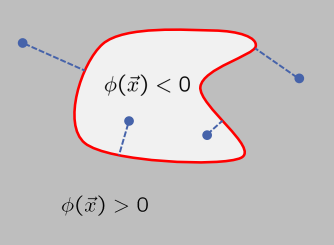
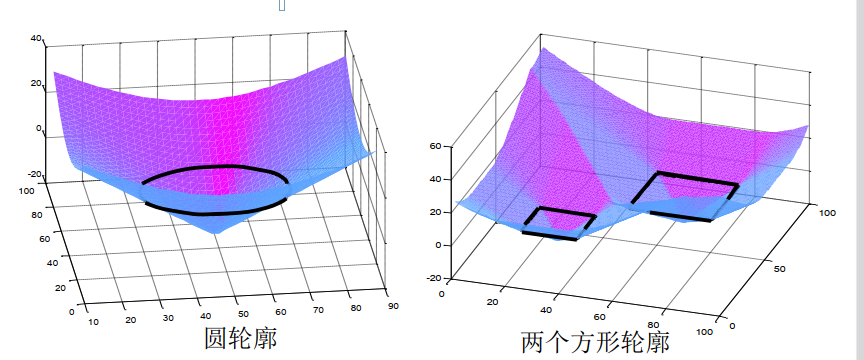
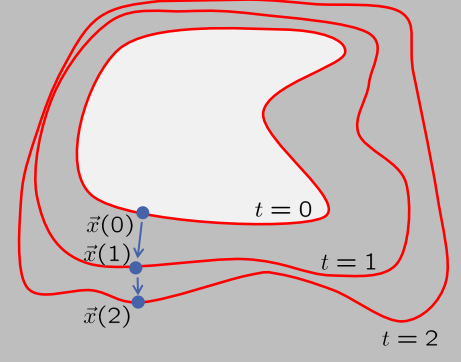
对有符号距离函数的时间演化建模: \(\phi(\vec{x}, t)\)
随着时间的推移跟踪边界上的一个点\(\vec{x}(t)\)
显然:
\[\phi(\vec{x}(t), t)=0\]for all \(t\)
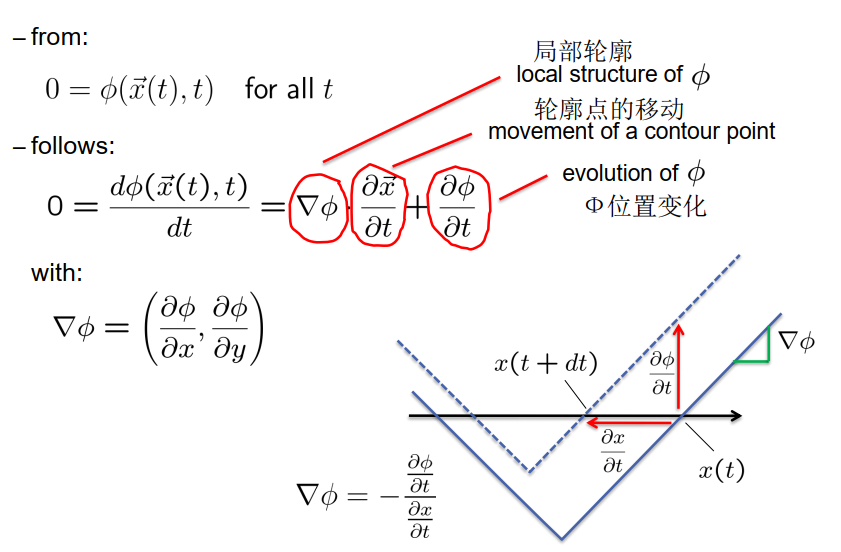
由上可得:
\[\frac{\partial \phi}{\partial t}=-\nabla \phi \cdot \frac{\partial \vec{x}}{\partial t}\]水平集方法的基本思想:
-
初始化:\(\phi(\cdot, 0)\)
-
合理假设:\(\frac{\partial \vec{x}}{\partial t}\)
-
随着时间跟随:\(\phi(\cdot, t)\)
使用数值积分实现,例如欧拉逼近(棘手!)
与轮廓正交的演化:
\[\begin{aligned} \frac{\partial \vec{x}}{\partial t} &=\alpha \cdot \frac{\nabla \phi}{\|\nabla \phi\|} \\ \frac{\partial \phi}{\partial t} &=-\nabla \phi \cdot \alpha \cdot \frac{\nabla \phi}{\|\nabla \phi\|} \\ &=-\alpha \frac{\|\nabla \phi\|^{2}}{\|\nabla \phi\|}=-\alpha\|\nabla \phi\| \end{aligned}\]如果 α > 0, 轮廓扩张; 如果 α < 0, 轮廓收缩
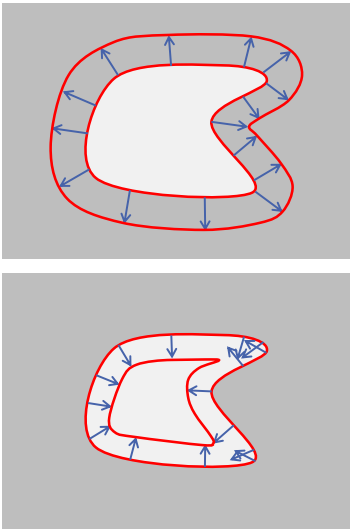
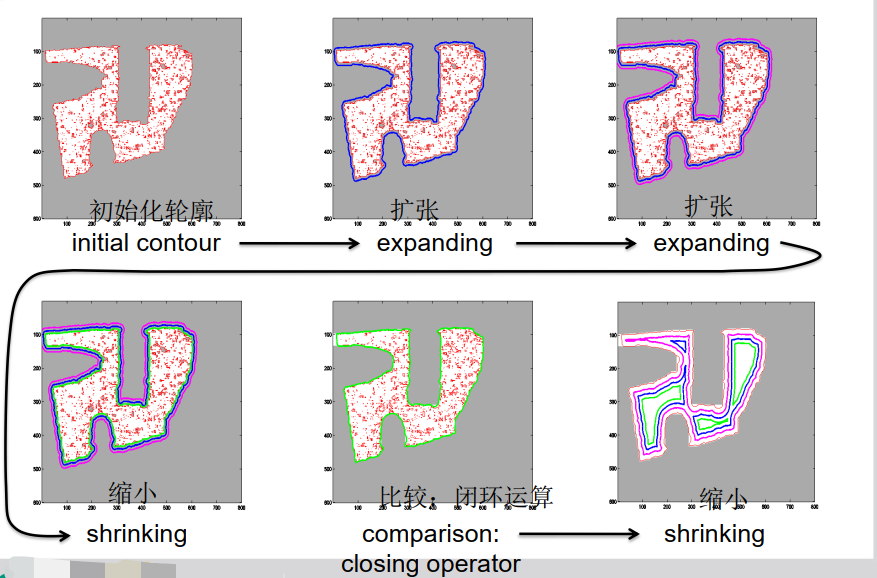
水平集演化可用于实现形态学运算:
膨胀 = 扩张
腐蚀 = 缩小
闭运算 = 缩小后扩张
开运算 = 扩张后缩小
使轮廓更加平滑
- 在凹陷的地方扩大
- 在凸面区域缩小
i演化水平集
- 正交于轮廓线
- 取决于局部曲率\(\kappa\)
在凸区域:局部近似轮廓的圆 \(\kappa = 1/r\)
在凹面区域:局部近似轮廓的圆\(\kappa = -1/r\)
一般来说:\(\kappa=\nabla\left(\frac{\nabla \phi}{\|\nabla \phi\|}\right)\)
level set update: 水平集升级:
\(\frac{\partial \vec{x}}{\partial t}=-\beta \kappa \frac{\nabla \phi}{\|\nabla \phi\|}\) \(\frac{\partial \phi}{\partial t}=\beta \kappa\|\nabla \phi\|\)
对黑白图非常简单的想法:
- 从一个非常大的轮廓线开始
- 在白色像素处缩减轮廓线
- 不要在黑色像素处收缩
轮廓包围黑色区域:
\[\frac{\partial \vec{x}}{\partial t}= \begin{cases}-\gamma \cdot \frac{\nabla \phi}{\|\nabla \phi\|} & \text { if white pixel } \\ 0 & \text { if black pixel }\end{cases}\]
将分割与轮廓矫正相结合
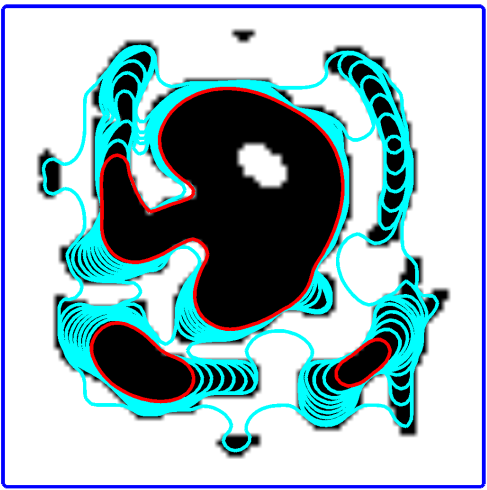
基于梯度的图像分割方法。
- 从一个非常大的轮廓线开始
- 在梯度长度小的像素处缩小轮廓
- 在梯度长度大的像素处不收缩(边缘像素)。 → 等高线包裹边缘的区域
with appropriate \(\gamma>0, p \geq 1\) \(g\)denotes gray level image
基于 Mumford-Shah 的分割
理念:像素应被分配到具有最相似分割的灰度值(颜色值)。
\(\bar{g}_{\text {foreground }}\):前景段像素的平均灰度值(颜色)
\(\bar{g}_{\text {background }}\):背景段中像素的平均灰度值(颜色)

用灰色(颜色)值检查边界上的像素 Ⅰ
-
像素更类似于外部区域 缩小轮廓
-
像素更类似于外部区域:
\[\left(g-\bar{g}_{\text {foreground }}\right)^{2}<\left(g-\bar{g}_{\text {background }}\right)^{2}\]扩张轮廓
基于 Mumford-Shah 的分割:

随机场
- 每个像素属于一个分割。 但是哪一个?

每个像素的分段标签被看作是一个变量
-
像素的特征向量与其标签有关

像素的特征向量也被视为变量,然而,它的值是被观察到的
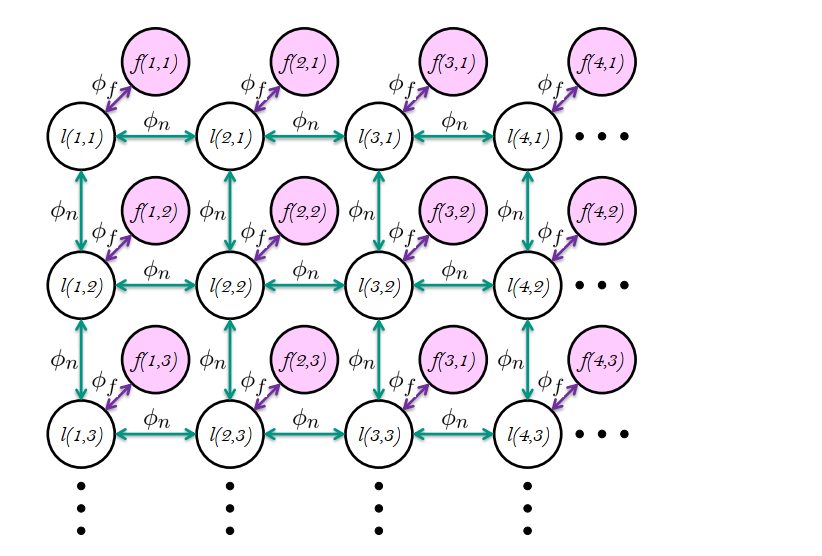
相邻像素的标签也相关
\(l(u, v) \leftrightarrow l(u+1, v)\) \(l(u, v) \leftrightarrow l(u, v+1)\)
该关系再次由势函数建模
\(\phi_{n}(l(u, v), l(u+1, v))\) \(\phi_{n}(l(u, v), l(u, v+1))\)
\[\phi_{n}(l(u, v), l(u+1, v))\left\{\begin{array}{l}\text { is small } \\ \text { if } l(u, v) \text { and } l(u+1, v) \text { are similar } \\ \text { is large } \\ \text { if } l(u, v) \text { and } l(u+1, v) \text { are dissimilar }\end{array}\right.\]找到标签 l(u,v) 使得势函数最小化
\[\begin{aligned} \operatorname{minimize}_{l(\cdot, \cdot)} & \alpha_{f} \cdot \sum_{u, v} \phi_{f}(l(u, v), f(u, v)) \\ &+\alpha_{n} \cdot \sum_{u, v} \phi_{n}(l(u, v), l(u+1, v)) \\ &+\alpha_{n} \cdot \sum_{u, v} \phi_{n}(l(u, v), l(u, v+1)) \end{aligned}\]带权重因子\(\alpha_{f}, \alpha_{n}>0\)
优化问题的解决方案: 精确 → 困难(一般来说,存在例外);近似
例如:从深色背景中提取明亮的前景对象
\(l=0 \quad\) background \(l=1 \quad\) foreground \(f \quad\) gray value \(0 \leq f \leq 255\)
\[\begin{aligned} &\phi_{f}(l, f)=\left(l-\frac{1}{255} f\right)^{2} \\ &\phi_{n}\left(l, l^{\prime}\right)=\left(l-l^{\prime}\right)^{2} \end{aligned}\]实现分割标准。
- 预定的颜色标准
- 空间标准

随机场建模的优势。
- 分割问题被表述为优化问题
- 潜在函数允许对许多分割标准进行建模,例如
- 种子点 对种子点保持标签函数不变
-
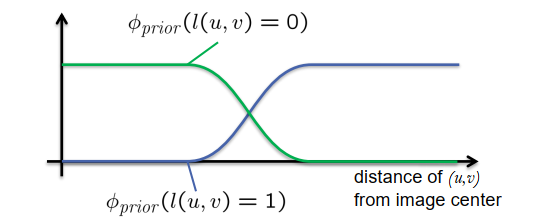
对某些分段标签的一般偏好(先验的)。 → 增加单项潜力函数 例如,指定前景物体应在图像的中心位置
原型分割特征向量。像素应该被分配到具有最相似原型特征向量的分割。 原型特征最相似的分割。 → 将原型变量添加到随机域中,每分割一个。 → 添加势函数,对原型特征和像素特征的相似性进行建模 f
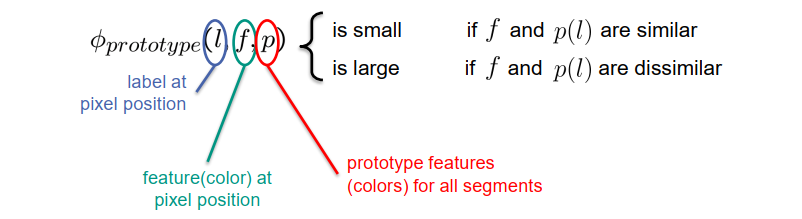
–>应用同质性标准
例如:
- 假设前景和背景的划分是
- 前景物体位于图像的中心位置
- 前景物体和背景物体具有独特的颜色
- 使用像素颜色(例如在RGB中)作为特征
\(\phi_{\text {prior }}(l(u, v))= \begin{cases}\max \left\{\frac{\mid 2 u-\text { width } \mid}{\text { width }}, \frac{\mid 2 v-\text { height } \mid}{\text { height }}\right\} & \text { if } l(u, v)=1 \\ 1-\max \left\{\frac{\mid 2 u-\text { width } \mid}{\text { width }}, \frac{|2 v-h e i g h t|}{\text { height }}\right\} & \text { if } l(u, v)=0\end{cases}$ $\phi_{\text {prototype }}(l, f, p)=\|f-p(l)\|^{2}\) \(\phi_{n}\left(l, l^{\prime}\right)=\left(l-l^{\prime}\right)^{2}\)
\[\begin{aligned} \operatorname{minimize}_{l(\cdot, \cdot), p(\cdot)} & \alpha_{\text {prior }} \cdot \sum_{u, v} \phi_{\text {prior }}(l(u, v)) \\ &+\alpha_{f} \cdot \sum_{u, v} \phi_{\text {prototype }}(l(u, v), f(u, v), p) \\ &+\alpha_{n} \cdot \sum_{u, v} \phi_{n}(l(u, v), l(u+1, v)) \\ &+\alpha_{n} \cdot \sum_{u, v} \phi_{n}(l(u, v), l(u, v+1)) \end{aligned}\]
