机器视觉-图像分割(第一部分)

在计算机视觉领域， 图像分割 （segmentation）指的是将数字图像细分为多个图像子区域（像素的集合）（也被称作超像素）的过程。图像分割的目的是简化或改变图像的表示形式，使得图像更容易理解和分析。图像分割通常用于定位图像中的物体和边界（线，曲线等）。更精确的，图像分割是对图像中的每个像素加标签的一个过程，这一过程使得具有相同标签的像素具有某种共同视觉特性。

图像分割在实际中的应用：

在卫星图像中定位物体（道路、森林等）

人脸识别

指纹识别

交通控制系统

刹车灯检测 Brake light detection

分割的准则

1. 预定义的颜色标准 predefined color criterion
2. 邻域准则 neighborhood criterion
3. 均匀性准则 homogeneity criterion
4. 连通性准则 connectedness criterion
5. 空间准则 spatial criterion
6. 边界光滑准则 boundary smoothness criterion
7. 尺寸准则 size criteria

预定义的颜色标准 predefined color criterion

像素颜色属于一组预定义的”有趣”的颜色，它指定了哪些颜色值是相关的，哪些像素是彩色的。

例如，我们在下面的足球机器人场地上找到橙色的球。

橙色的像素点是在HSV值在以下范围的：

$0^{\circ} \leq H \leq 24^{\circ}, 0.4 \leq S \leq 1,0.4 \leq V \leq 1$

注： HSV值(Hue, Saturation, Value)是是根据颜色的直观特性由A. R. Smith在1978年创建的一种颜色空间, 也称六角锥体模型(Hexcone Model)。这个模型中颜色的参数分别是：色调（H），饱和度（S），亮度（V）。

色调H：用角度度量，取值范围为0°～360°，从红色开始按逆时针方向计算，红色为0°，绿色为120°,蓝色为240°。它们的补色是：黄色为60°，青色为180°,品红为300°；

饱和度S：取值范围为0.0～1.0；

亮度V：取值范围为0.0(黑色)～1.0(白色)。

RGB和CMY颜色模型都是面向硬件的，而HSV（Hue Saturation Value）颜色模型是面向用户的。

HSV模型的三维表示从RGB立方体演化而来。设想从RGB沿立方体对角线的白色顶点向黑色顶点观察，就可以看到立方体的六边形外形。六边形边界表示色彩，水平轴表示纯度，明度沿垂直轴测量。

根据颜色进行分割的优缺点：

• 非常快速
• 如果事先知道物体的颜色，并且颜色具有辨别力，则可以应用
• 如果不同的对象共享相同的颜色，则不适用
• 找到合适的颜色规格通常很麻烦

邻域准则 neighborhood criterion

像素颜色与相邻像素的颜色相似，指定哪些颜色相似，将一段中的所有像素分组，这些像素至少有一个已属于该段的相邻像素

例如：如果RGB三元组的欧氏距离小于7/255，则像素是相邻的

根据邻域准则进行图片细分的优缺点：

• 简单
• 物体的颜色不需要知道
• 对象边界必须是高对比度，内部必须是低对比度
• 模糊的图像可能导致分段不足，嘈杂的图像可能导致分段过度

均匀性准则 homogeneity criterion

像素颜色与线段的分割颜色相似，指定如何计算平均的颜色并确定两种颜色是否相似。将所有像素分组到一段中，这些像素与分割的平均颜色相似

例如：与球的平均颜色相似的像素，都属于此分割颜色

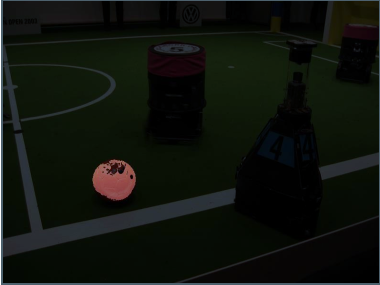
通过均匀性准测进行图像分割的优缺点：

• 物体的颜色不需要知道
• 对象的所有部分都必须具有相似的颜色
• 不支持低频率的颜色变化
• 循环定义

连通性准则 connectedness criterion

同一段中的所有像素必须连接，即在该段的两个像素之间有一条不离开该段的路径

优缺点：

此标准可以与其他标准相结合

空间准则 spatial criterion

被另一部分的像素包围的像素应该属于该部分（另一部分）

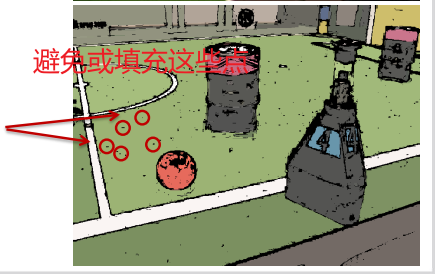
优缺点：

• 标准与其他标准相结合
• 提高了抗噪性

边界光滑准则 boundary smoothness criterion

分割的边界应平滑，而不是参差不齐。

优缺点：

• 标准与其他标准相结合
• 提高了抗噪性

尺寸准则 size criteria

分割的大小应在一定范围内/不太小/不太大

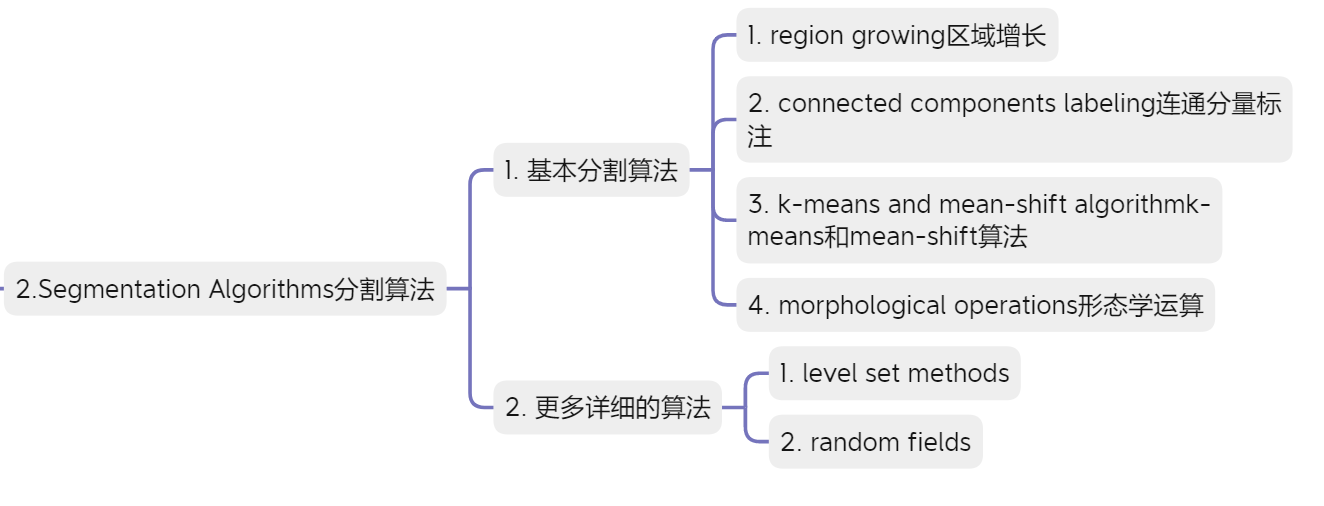
分割算法

基础算法：

1. 区域增长 region growing
2. 连接组件标记 connected components labeling
3. K-means和mean-shift算法
4. 形态学运算 morphological operations

更详尽的算法：

1.水平集方法 level set methods

2.随机场 random fields

区域增长 region growing

区域生长（region growing）是指将成组的像素或区域发展成更大区域的过程。从种子点的集合开始，从这些点的区域增长是通过将与每个种子点有相似属性像强度、灰度级、纹理颜色等的相邻像素合并到此区域。

区域生长算法的基本思想是将有相似性质的像素点合并到一起。对每一个区域要先指定一个种子点作为生长的起点，然后将种子点周围领域的像素点和种子点进行对比，将具有相似性质的点合并起来继续向外生长，直到没有满足条件的像素被包括进来为止。这样一个区域的生长就完成了。这个过程中有几个关键的问题：（原文链接：https://blog.csdn.net/weixin_40647819/article/details/90215872）

核心思想：从一个/多个种子点开始（必须提供种子点）；增量扩展段，直到无法添加更多像素；实现连通性标准+同质性或邻域标准；产生单一的片段。

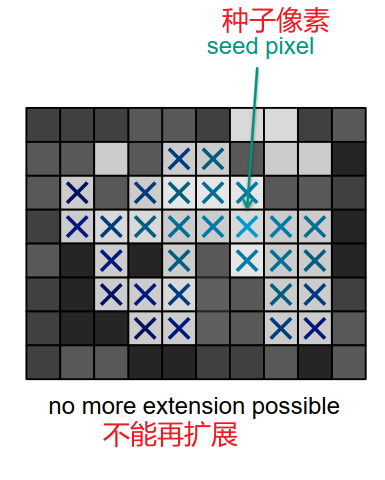
优缺点：

• 易于实现（广度优先搜索）
• 需要一个或多个种子点

连接组件标记算法 connected components labeling（CCL）

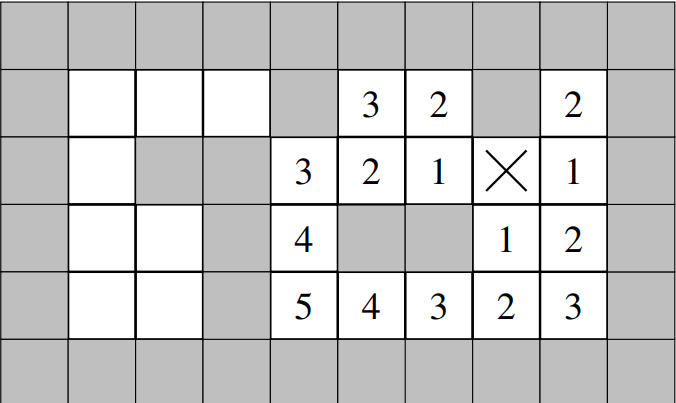
连接组件标记算法(connected component labeling algorithm)是图像分析中最常用的算法之一，算法的实质是扫描一幅图像的每个像素，对于像素值相同的分为相同的组(group),最终得到图像中所有的像素连通组件。 扫描的方式可以是从上到下，从左到右，对于一幅有N个像素的图像来说，最大连通组件个数为N/2。扫描是基于每个像素单位，对于二值图像而言，连通组件集合可以是V={1|白色}或者V={0|黑色}, 取决于前景色与背景色的不同。 对于灰度图像来说，连图组件像素集合可能是一系列在0 ～ 255之间k的灰度值。

引用自：知乎

核心思想：创建图像的完整分割；实现连通性标准+邻域标准；仅通过确定与两个相邻像素的相似性，将每个像素分配给分段

我们从左上角到右下角逐行访问像素，并立即将它们分配给一个段。

当我们访问一个像素（u，v）时，我们已经访问了（u-1，v）和（u，v-1）。我们比较颜色（u，v）和颜色（u-1，v），颜色（u，v-1），五种情况：

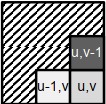
1. （u，v）和（u-1，v）处的像素颜色相似，（u，v）和（u，v-1）处的像素颜色不同

   → 像素（u，v）和（u-1，v）属于同一段

   → 我们将像素（u，v）分配给像素（u-1，v）的部分

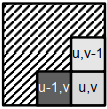
1. （u，v）和（u-1，v）处的像素颜色不同，（u，v）和（u，v-1）处的像素颜色相似

   → 像素（u，v）和（u，v-1）属于同一段

   → 我们将像素（u，v）分配给像素（u，v-1）的部分

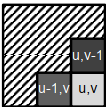
1. （u，v）和（u-1，v）处的像素颜色不同，（u，v）和（u，v-1）处的像素颜色不同

   → 为什么像素（u，v）应该属于（u-1，v）或（u，v-1）的段？

   → 我们创建一个新段，并为其指定像素（u，v）

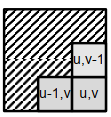
1. （u，v）和（u-1，v）处的像素颜色是相似的，（u，v）和（u，v-1）处的像素颜色是相似的，像素（u-1，v）和（u，v-1）属于同一段。

   → 像素（u，v）也属于该部分

   → 我们将像素（u，v）分配给该段

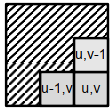
1. （u，v）和（u-1，v）处的像素颜色相似，（u，v）和（u，v-1）处的像素颜色相似，像素（u-1，v）和（u，v-1）不属于同一段

   → 像素（u，v）属于两个相邻的部分

   → 我们合并两个相邻的段，并将像素（u，v）分配给合并的段

K均值聚类算法 K-means

k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

核心思想：图像由相似颜色的区域组成; 寻找颜色的簇; 将每个像素指定给其颜色簇; 实现同质性标准; 创建完整的分割。

在上面图片中的颜色簇：绿色，白色，橙色，黑色，品红，蓝，黄色，灰色

怎么找到颜色簇呢？ 如果我们知道簇的数量 –> k-means 算法

1. 随机初始化k原型颜色c1、c2、…、ck（例如，从图像中随机选取像素）
2. 将每个像素指定给最相似的原型颜色
3. 通过对步骤2中指定的像素颜色进行平均，重新计算原型颜色
4. 重复第2步和第3步，直到收敛（即第2步中的赋值不再改变）

例如：

第1步：从两个像素中随机选择颜色；

第2步：将像素分配给最相似的簇；

第3步：重新计算原型颜色；

第2步：重新分配像素；

第3步：重新计算原型颜色；

第2步：重新分配像素→ 汇聚

k-均值算法

优点：

•简单、易于实现

缺点：

•必须知道聚类数（k）

•通常会收敛到次优聚类（取决于初始原型颜色）

未知聚类数的改进： mean-shift 均值漂移

• 需要颜色的相似性度量
• 对于每个像素p，按如下步骤进行： 1.确定p的颜色并将其分配给变量c
  1. 找到图像中与c相似的所有像素的集合S
  2. 计算S的平均颜色并将其分配给变量c（不要改变图像中p的像素值 不要改变图像中p的像素值！)
  3. 重复步骤2和3，直到收敛（即直到步骤2中的S保持不变）。
  4. 最后，c是像素p所属区段的原型颜色。

示例: 沿一个轴排列所有像素颜色（灰度值）

第1步：选择目标像素的颜色并初始化c 第2步：找到相似像素的集合S 第3步：计算S的平均颜色并将其分配给c 第2步：重新计算S 第3步：重新计算S的平均颜色并将其分配给c 第2步：重新计算S 第3步：重新计算S的平均颜色并将其分配给c 第2步：重新计算S→收敛