深度学习 Deep Learning
多层感知器Multi-Layer Perceptrons (MLP)
MLP 是高度参数化的非线性函数
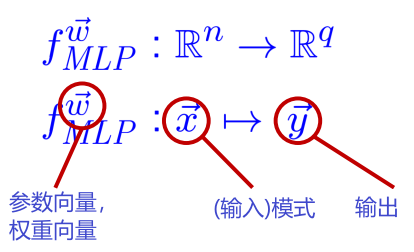
示例:图像分类

$\vec{x}$ 特征向量,例如 图像中所有灰度值的向量
$\vec{y}$ 1-of-q-vector 为 q 个可能类别中的每一个建模概率,例如 笑脸是快乐/悲伤/沮丧
感知器, 感知机
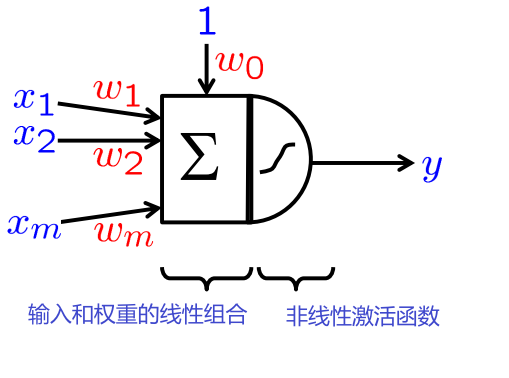
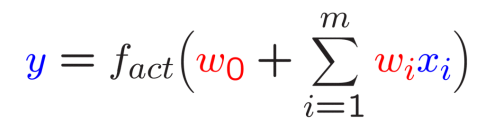
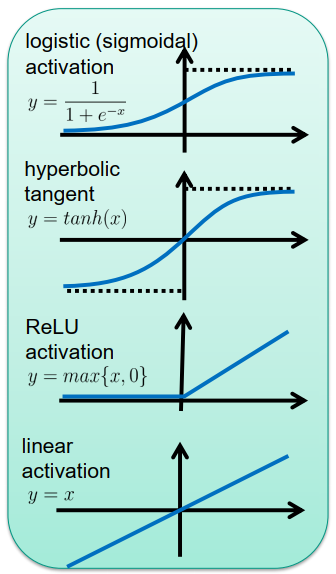
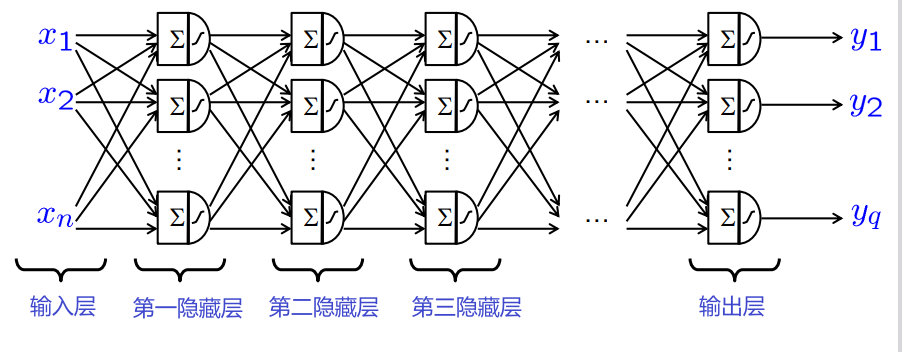
许多感知器的分层排列:
-
网络结构创建了一组高度非线性的函数
- 许多权重
- 深层架构:通常 >5 个隐藏层
我们如何确定 MLP 的权重?
– 基本思想:最小化训练样例的误差
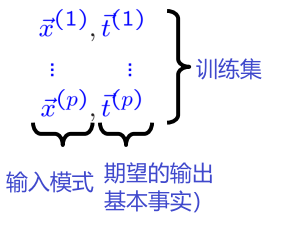
解决
\[\operatorname{minimize}_{\vec{w}} \sum_{j=1}^{p} \operatorname{err}\left(f_{M L P} ^ {\vec{w} }\left(\vec{x}^ {(j)}\right), \vec{t}^ {(j)}\right)\]用于适当的误差测量(损失函数)
for appropriate error measure (loss function)
算法:梯度下降(反向传播)
梯度下降(反向传播)Gradient Descent (Backpropagation)
目标:
\[\underset{\vec{w}} {\operatorname{minimize}} g(\vec{w}) \text { with } g(\vec{w}):=\sum_{j=1}^{p} \operatorname{err}\left(f_{M L P}^{\vec{w} }\left(\vec{x}^{(j)}\right), \bar{t}^{(j)}\right)\]算法:
- 用小数字随机初始化权重 $\vec{w}$
- 计算梯度 $\frac{\partial g(\vec{w})}{\partial \vec{w}}$
- 以小的学习率$\varepsilon>0$更新权重 $\varepsilon>0\vec{w} \leftarrow \vec{w}-\varepsilon \frac{\partial g(\vec{w})}{\partial \vec{w}}$
- 转到 第2步 直到达到停止标准
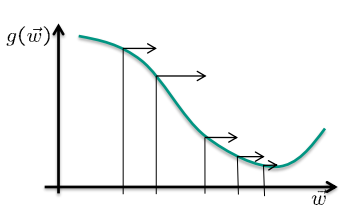
改进: – 稍后讨论
训练 MLP(传统方法)Training MLPs (traditional methods)
传统训练方法的问题:
- 权重太多,训练样例太少
- 太慢
- 数值问题,局部最小值
👉过拟合、欠拟合、泛化不足
克服问题的传统技术:
- 正则化(例如提前停止、权重衰减、贝叶斯学习)
- 模式预处理、特征提取、降维
- 选择更小的 MLP、更少的层、更少的隐藏神经元、网络修剪
- 用其他方法替换神经网络 (例如 SVM、boosting 等)
深度学习
深度学习有什么不同的?
- 更大的训练集(数百万而不是数百)
-
更强大的计算机,多核 CPU 和 GPU 上的并行实现
-
特殊网络结构
自编码器
卷积网络
循环网络/LSTM
(深度信念网络/受限玻尔兹曼机)
…
- 权重共享 weight sharing
- 逐层学习 layer-wise learning
- Dropout
- 有用特征的学习 learning of useful features
- 从无标签的例子中学习 learning from unlabeled examples
特征学习
观察:
- 许多像素并没有提供太多的信息
- 相邻的像素是高度相关的
示例:笑脸
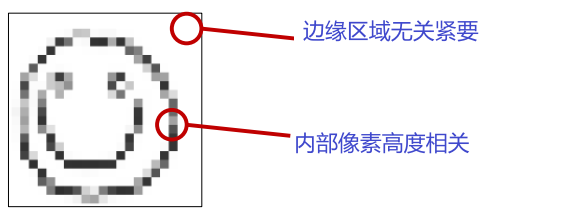
我们如何将相关信息与无关信息分开?
自动编码器 Autoencoder
👉具有这种结构的 MLP
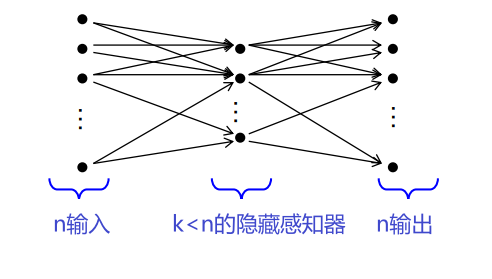
学习识别功能:
\[\operatorname{minimize}_{\vec{w}} \sum_{j=1}^{p}\left(f_{M L P}^{\vec{w}}\left(\vec{x}^{(j)}\right)-\vec{x}^{(j)}\right)^{2}\]隐蔽层必须分析压缩图像内容的神经主成分的种类
堆叠自动编码器 Stacked Autoencoders
多层自动编码器的增量训练
-
训练具有单个隐藏层的自动编码器
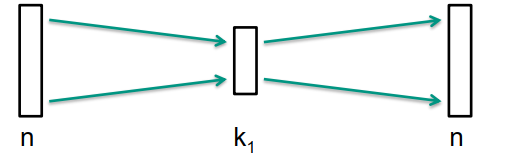

-
通过附加隐藏层扩展自动编码器
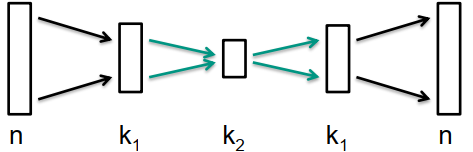

-
类似地重复过程以添加更多隐藏层
👉信息压缩逐层增加非线性、多层主成分分析
用于分类的堆叠自动编码器
- 训练堆叠自动编码器
- 用全连接分类器网络替换解码器网络
- 训练分类器网络
- 训练编码器和分类器网络的所有权重进行几次迭代
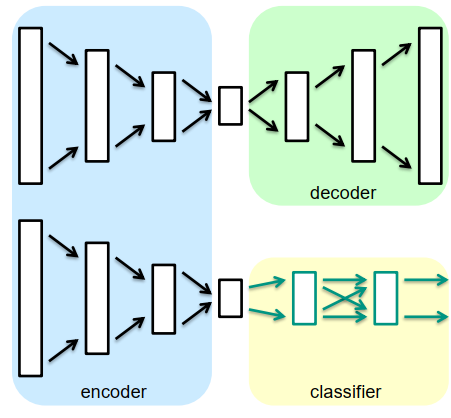
优点:
- 堆叠式自动编码器可以使用未标记的示例进行训练
- 增量训练获得更好的结果
局部感受野Local Receptive Fields
评论里有句话:convNets(cnn)每一层输出的特征图(feature map)上的像素点在原始图像上映射的区域大小。
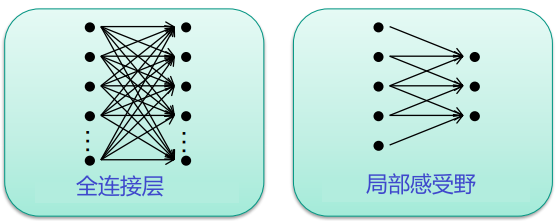
局部感受野迫使网络在本地处理信息。
示例:图像的局部特征
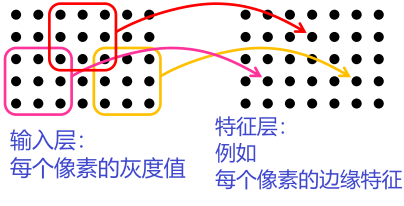
权值共享 Weight Sharing
权值共享就是说,给一张输入图片,用一个卷积核去扫这张图,卷积核里面的数就叫权重,这张图每个位置是被同样的卷积核扫的,所以权重是一样的,也就是共享。
我们可以为所有像素生成相同的局部特征吗?
- 权重共享:绑定不同感知器的权重
- 卷积层:绑定一层所有感知器的权重
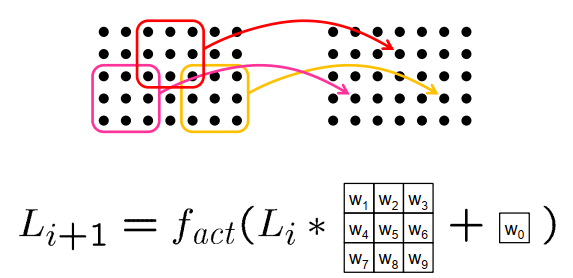
多通道特征层Multi-Channel Feature Layers
在每个隐藏层中,想为每个像素计算几个不同的特征 → 多通道层
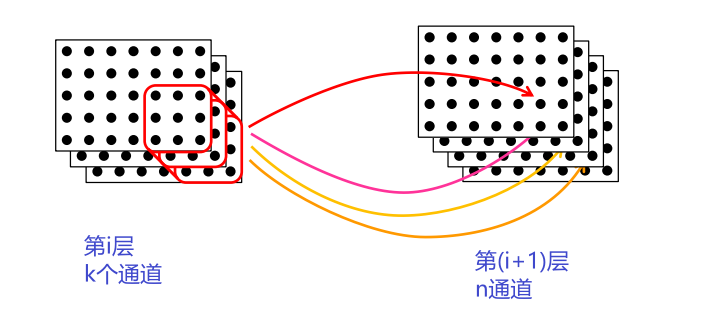
卷积核是大小$h×w×k$的张量
最大池化Max-Pooling
池化层旨在在空间上聚合信息
池化(Pooling)是卷积神经网络中的一个重要的概念,它实际上是一种形式的降采样。有多种不同形式的非线性池化函数,而其中“最大池化(Max pooling)”是最为常见的。它是将输入的图像划分为若干个矩形区域,对每个子区域输出最大值。直觉上,这种机制能够有效的原因在于,在发现一个特征之后,它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小,因此参数的数量和计算量也会下降,这在一定程度上也控制了过拟合。通常来说,CNN的卷积层之间都会周期性地插入池化层。
Max-Pooling:从局部感受野计算最大值
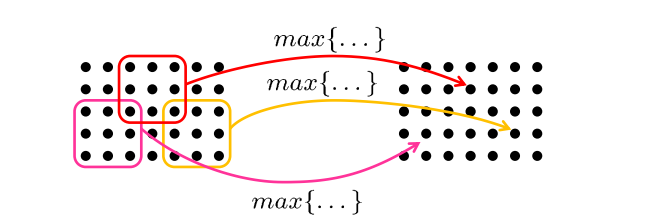
池化通常与降低层的分辨率相结合
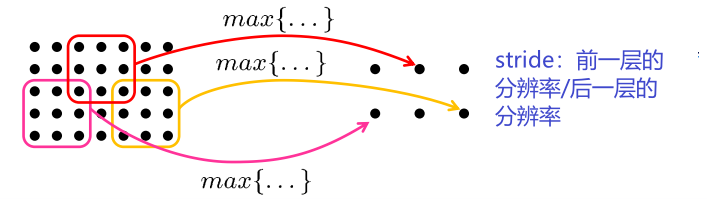
卷积网络Convolutional Networks
卷积神经网络(CNN)结合了
- 卷积层
- 池化层
- 全连接分类器网络
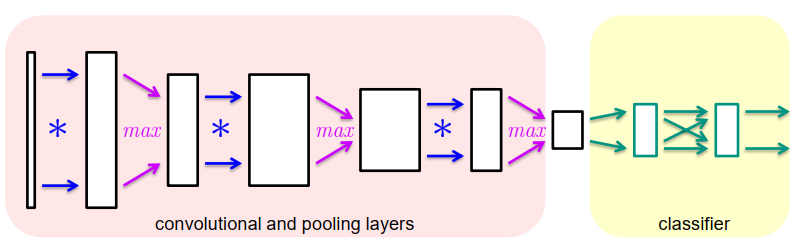
例如:Alexnet是2012年Imagenet竞赛的冠军模型,准确率达到了57.1%, top-5识别率达到80.2%。
AlexNet包含5个卷积层和3个全连接层,模型示意图:
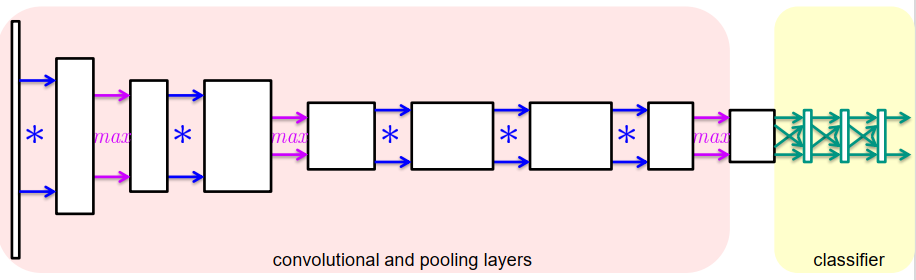
从层到层… – 特征在几何上变得越来越复杂 – 特征变得越来越独立于位置 – 特征变得越来越独立于图案大小 – 特征变得越来越具体
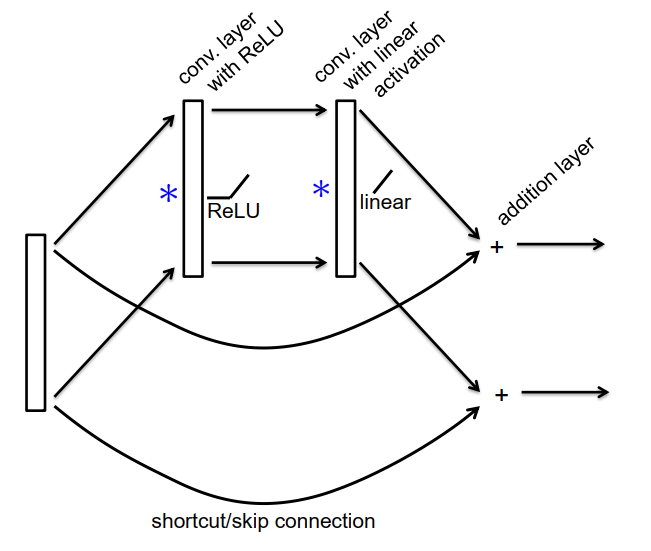
ResNet层 ResNet Layers