针孔照相机
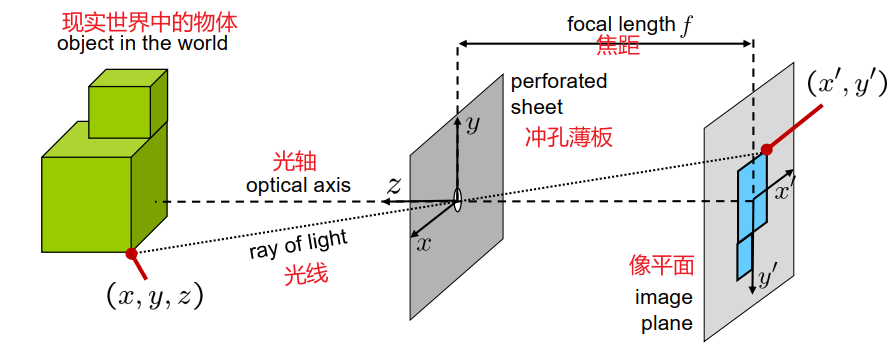
点\((x,y,z)\)投影到\((x',y')\)截距定理:
\[\frac{x}{z}=\frac{x^{\prime}}{f}, \quad \frac{y}{z}=\frac{y^{\prime}}{f} \quad \Rightarrow \quad z \cdot\left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)=\left(\begin{array}{ll}f & 0 \\ 0 & f\end{array}\right) \cdot\left(\begin{array}{l}x \\ y\end{array}\right)\]世界到图像映射
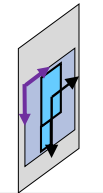
相机坐标系
图像坐标系
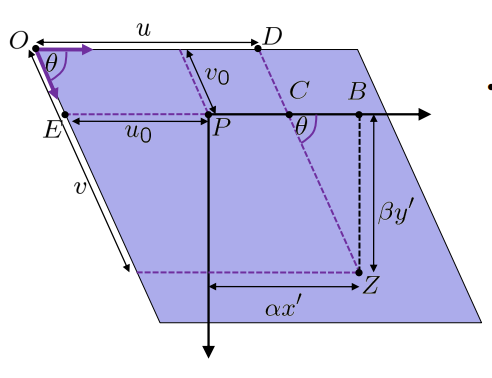
- u 方向平行于 x’ 方向
- v 方向可能倾斜 θ=u 和 v 方向之间的角度
- 主点 = 图像坐标中相机坐标系的原点 (u0,v0)
- 单位向量 u 和 v 的长度与单位向量 x’、y’ 的长度不同 比例因子 α、β
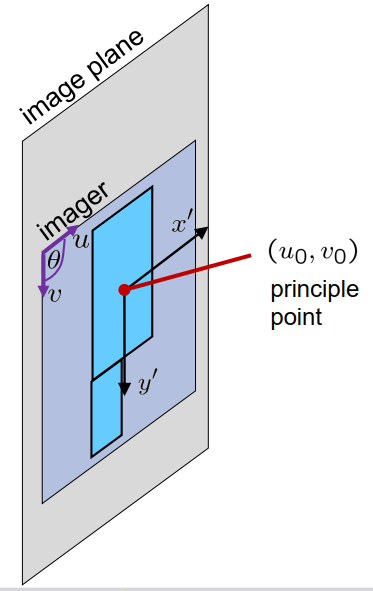
将点 Z 从相机坐标映射到图像坐标:
三角形 ZBC:
\[\begin{aligned} \sin \theta &=\frac{\beta y^{\prime}}{v-v_{0}} \\ \Rightarrow v &=\frac{\beta}{\sin \theta} y^{\prime}+v_{0} \\ \cot \theta &=\frac{\alpha x^{\prime}+u_{0}-u}{\beta y^{\prime}} \\ \Rightarrow u &=\alpha x^{\prime}-(\cot \theta) \cdot \beta y^{\prime}+u_{0} \end{aligned}\]==从相机到图像帧的映射:==
 \(\left(\begin{array}{l}
u \\
v
\end{array}\right)=\left(\begin{array}{cc}
\alpha & -\beta \cot \theta \\
0 & \frac{\beta}{\sin \theta}
\end{array}\right) \cdot\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)+\left(\begin{array}{l}
u_{0} \\
v_{0}
\end{array}\right)\)
\(\left(\begin{array}{l}
u \\
v
\end{array}\right)=\left(\begin{array}{cc}
\alpha & -\beta \cot \theta \\
0 & \frac{\beta}{\sin \theta}
\end{array}\right) \cdot\left(\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right)+\left(\begin{array}{l}
u_{0} \\
v_{0}
\end{array}\right)\)
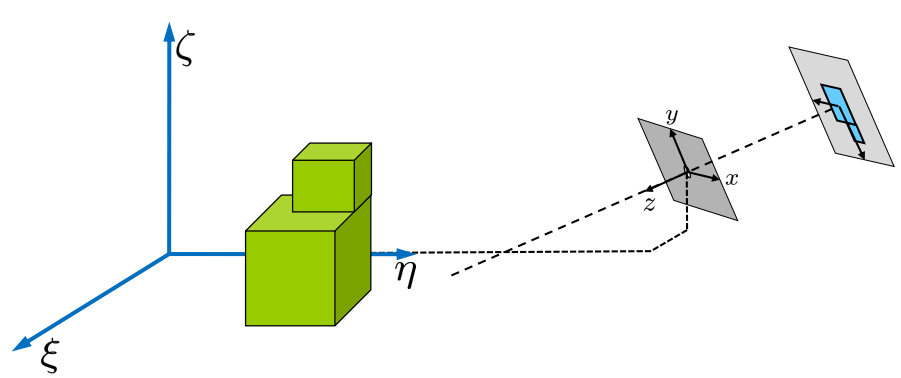
物体在相机坐标上的位置通常未知
外部坐标系(“世界框架”)(ξ,η,ζ)
映射: \(\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=R \cdot\left(\begin{array}{l} \xi \\ \eta \\ \zeta \end{array}\right)+\vec{t}\) R是旋转矩阵,t是转移矩阵
-
坐标变换
世界框架→相机框架
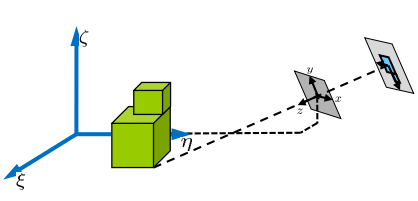
- 透视投影;中心投影法
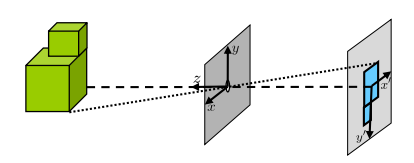
- 坐标变换
相机帧→图像帧 \(\left(\begin{array}{l} u \\ v \end{array}\right)=\left(\begin{array}{cc} \alpha & -\beta \cot \theta \\ 0 & \frac{\beta}{\sin \theta} \end{array}\right) \cdot\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right)+\left(\begin{array}{l} u_{0} \\ v_{0} \end{array}\right)\) \(cot\theta=cos\theta/sin\theta\)
重写步骤3:
\(\left(\begin{array}{l}
u \\
v \\
1
\end{array}\right)=\left(\begin{array}{ccc}
\alpha & -\beta \cot \theta & u_{0} \\
0 & \frac{\beta}{\sin \theta} & v_{0} \\
0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
1
\end{array}\right)\)
重写步骤2:
\(z \cdot\left(\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
1
\end{array}\right)=\left(\begin{array}{lll}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)\)
结合第 2 步和第 3 步:
\(\begin{aligned}
z \cdot\left(\begin{array}{l}
u \\
v \\
1
\end{array}\right) &=\left(\begin{array}{ccc}
\alpha & -\beta \cot \theta & u_{0} \\
0 & \frac{\beta}{\sin \theta} & v_{0} \\
0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{lll}
f & 0 & 0 \\
0 & f & 0 \\
0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right) \\
&=\left(\begin{array}{ccc}
f \alpha & -f \beta \cot \theta & u_{0} \\
0 & \frac{f \beta}{\sin \theta} & v_{0} \\
0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right) \\
&=\underbrace{\left(\begin{array}{ccc}
\alpha^{\prime} & -\beta^{\prime} \cot \theta & u_{0} \\
0 & \frac{\beta^{\prime}}{\sin \theta} & v_{0} \\
0 & 0 & 1
\end{array}\right)}_{=: A} \cdot\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)
\end{aligned}\)
with
\(\alpha^{\prime}=f \alpha, \quad \beta^{\prime}=f \beta\)
重写步骤1:
\(\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=(R \mid \vec{t}) \cdot\left(\begin{array}{l}
\xi \\
\eta \\
\zeta \\
1
\end{array}\right)\)
将 1 与之前的结果相结合:
给定 (ξ,η,ζ),我们如何计算 (u,v) ?
\[\begin{array}{l} \left(\begin{array}{c} \tilde{x} \\ \tilde{y} \\ \tilde{z} \end{array}\right)=A \cdot(R \mid \vec{t}) \cdot\left(\begin{array}{l} \xi \\ \eta \\ \zeta \\ 1 \end{array}\right) \\ \left(\begin{array}{l} u \\ v \end{array}\right)=\frac{1}{\widetilde{z}}\left(\begin{array}{l} \tilde{x} \\ \tilde{y} \end{array}\right) \end{array}\]给定 (u,v),我们如何计算 (ξ,η,ζ) ?
\[\left(\begin{array}{l} \xi \\ \eta \\ \zeta \end{array}\right)=z R^{T} A^{-1}\left(\begin{array}{l} u \\ v \\ 1 \end{array}\right)-R^{T} \vec{t} \quad \text { with } z \geq 0\](ξ,η,ζ) 不是唯一的,而是射线的元素
相机原点坐标:
\[(\xi, \eta, \zeta)^{T}=-R^{T} \vec{t}\]参数:
-
内在参数:描述相机(5个参数)
\[u_{0}, v_{0}, \alpha^{\prime}, \beta^{\prime}, \theta\] -
外部参数:相机的位姿(6个参数)
\[R,\vec{t}\] -
有时,模型被简化假设
体积测量
测量体积:
– 是一个矩形金字塔
– 焦点是金字塔的顶点
– 水平孔径角(张角)
\[\arccos \frac{\left\langle A^{-1}\left(0, v_{0}, 1\right)^{T}, A^{-1}\left(u_{\max }, v_{0}, 1\right)^{T}\right\rangle}{\left\|A^{-1}\left(0, v_{0}, 1\right)^{T}\right\| \cdot\left\|A^{-1}\left(u_{\max }, v_{0}, 1\right)^{T}\right\|}\]– 垂直孔径角
\[arccos \frac{\left\langle A^{-1}\left(u_{0}, 0,1\right)^{T}, A^{-1}\left(u_{0}, v_{\max }, 1\right)^{T}\right\rangle}{\left\|A^{-1}\left(u_{0}, 0,1\right)^{T}\right\| \cdot\left\|A^{-1}\left(u_{0}, v_{\max }, 1\right)^{T}\right\|}\]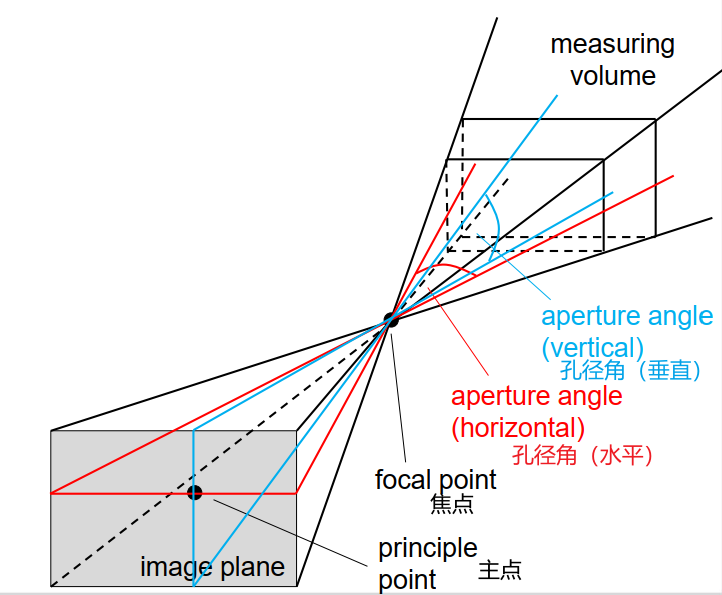
透视投影;中心投影法



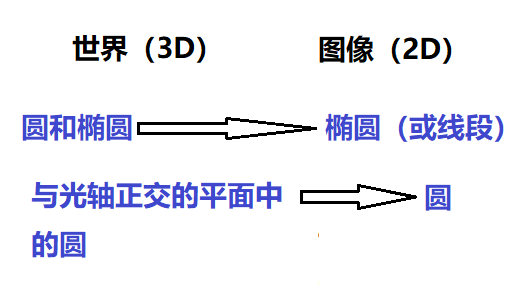

透视投影不:
– 保留角度
– 保留长度
– 保留面积
– 保留长度比
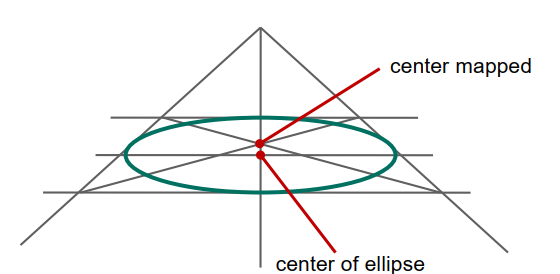
– 将圆/椭圆的中心映射到所映射的椭圆的中心(除非:如果平面与光轴正交)
镜头
针孔相机很难让光线通过
→ 镜头 • 斯涅尔折射定律
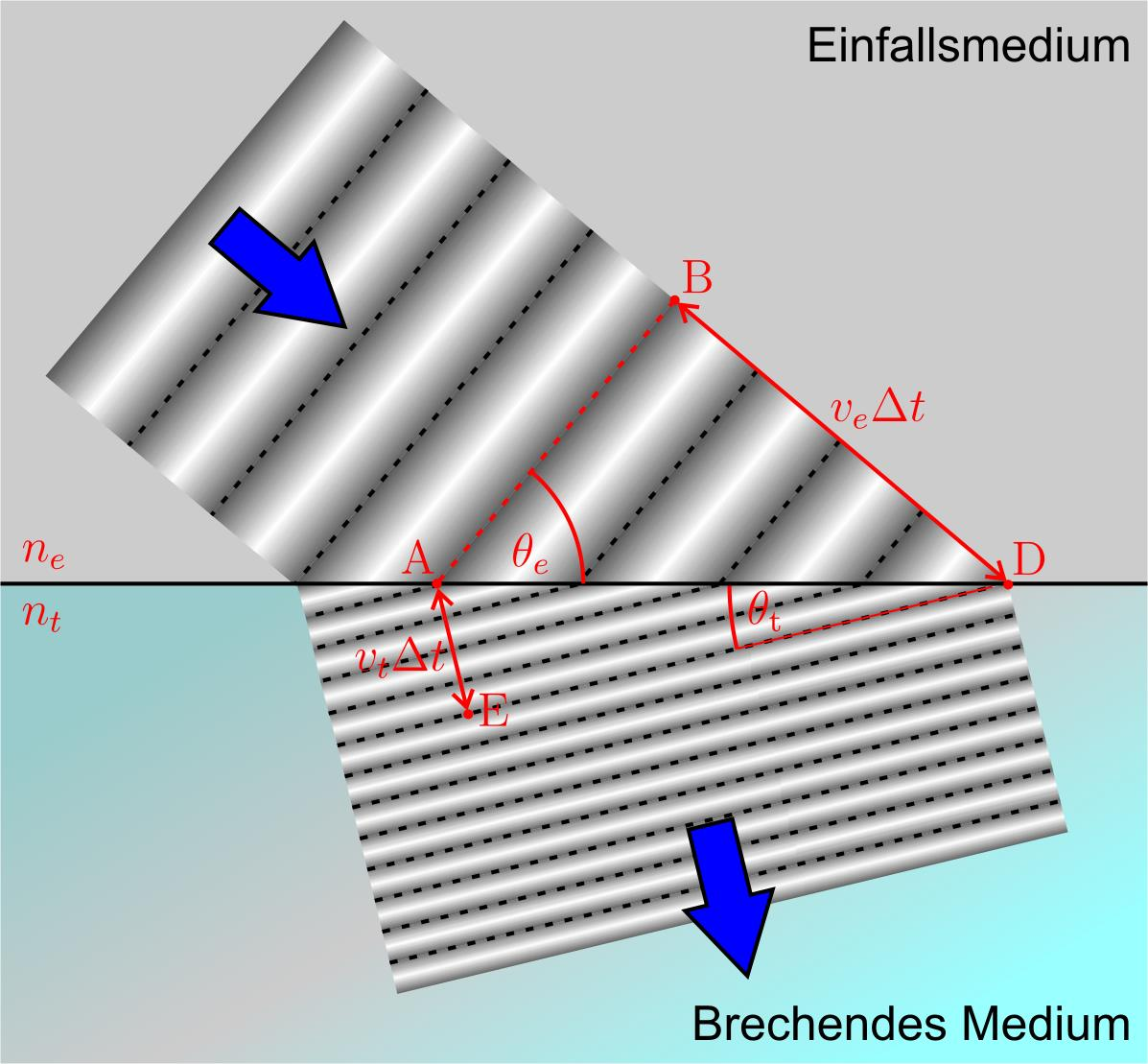
📌Snell’s law: 📌
\[n_{e} \sin \theta_{e}=n_{t} \sin \theta_{t}\] \[n_{\text {medium }}=\frac{v_{\text {vacuum }}}{v_{\text {medium }}}\]镜头焦距:镜头到焦点的距离,平行于光轴的光线被折射后的交汇点
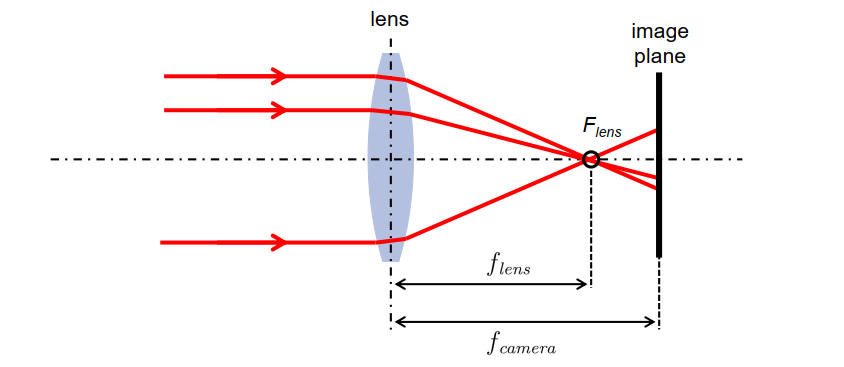
镜片的折射
– 表面空气/玻璃
– 表面玻璃/空气
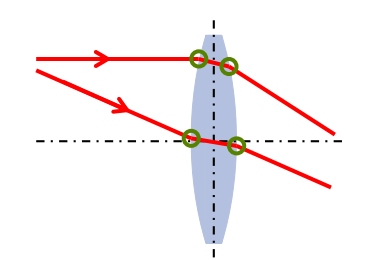
- 可忽略的厚度
- 双折射可以通过中心线的单折射来近似
- 更简单的几何建模

薄镜片
清晰的图像必须满足什么条件?
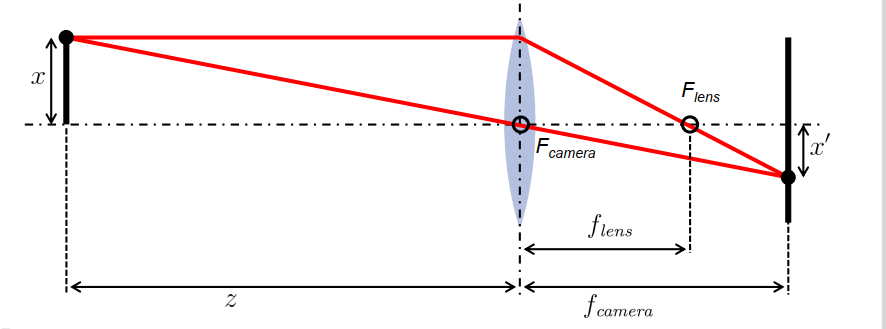
截距定理:
\[\frac{x^{\prime}}{x}=\frac{f_{\text {camera }}}{z}\] \[\frac{x^{\prime}}{x}=\frac{f_{\text {camera }}-f_{\text {lens }}}{f_{\text {lens }}}\]由上可得 👉
\[\frac{1}{f_{\text {lens }}}=\frac{1}{f_{\text {camera }}}+\frac{1}{z}\](透镜方程)
当违反透镜方程时会发生什么?
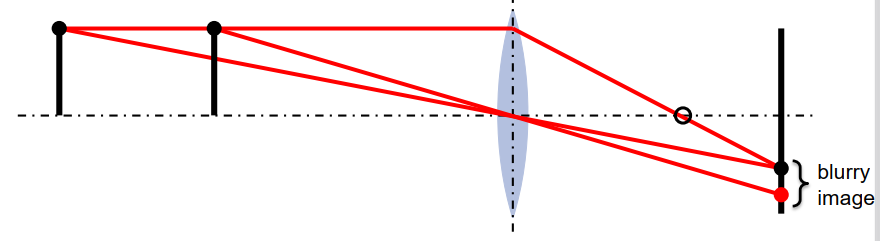
我们可以改变z多少程度才影响不大?
Depth of Field 景深;视野深度
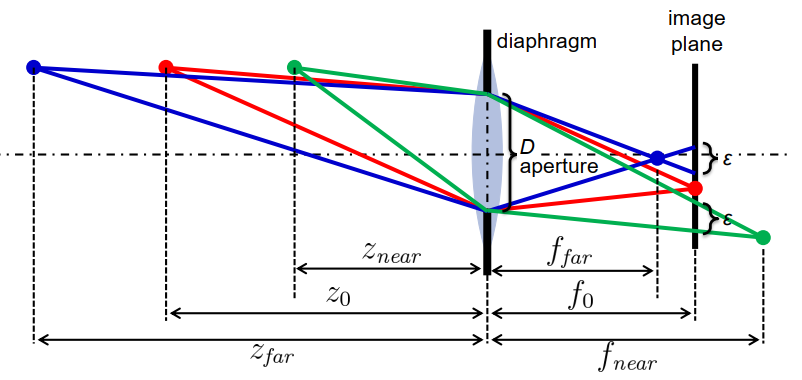
截距定理:
\[\frac{\epsilon}{D}=\frac{f_{0}-f_{f a r}}{f_{f a r}}=\cdots=\frac{f_{\text {lens }} \cdot\left(z_{\text {far }}-z_{0}\right)}{z_{\text {far }} \cdot\left(z_{0}-f_{\text {lens }}\right)}\]截距定理:
\[\frac{\epsilon}{D}=\frac{f_{\text {near }}-f_{0}}{f_{\text {near }}}=\cdots=\frac{f_{\text {lens }} \cdot\left(z_{0}-z_{\text {near }}\right)}{z_{\text {near }} \cdot\left(z_{0}-f_{\text {lens }}\right)}\]由上可得:
\[z_{f a r}=\frac{z_{0} \cdot d_{h}}{d_{h}-\left(z_{0}-f_{l e n s}\right)}\] \[z_{\text {near }}=\frac{z_{0} \cdot d_{h}}{d_{h}+\left(z_{0}-f_{\text {lens }}\right)}\]\(d_{h}=\frac{D \cdot f_{\text {lens }}}{\epsilon}\)(hyperfocal distance) (超焦距)
\[\Delta z=z_{\text {far }}-z_{\text {near }}=2 \frac{z_{0} \cdot d_{h} \cdot\left(z_{0}-f_{\text {lens }}\right)}{d_{h}^{2}-\left(z_{0}-f_{\text {lens }}\right)^{2}}\]观察:
对于
\[z_{0} \rightarrow d_{h}+f_{\text {lens }}\]holds:
\[z_{\text {far }} \rightarrow \infty\] \[\Delta z \rightarrow \infty\]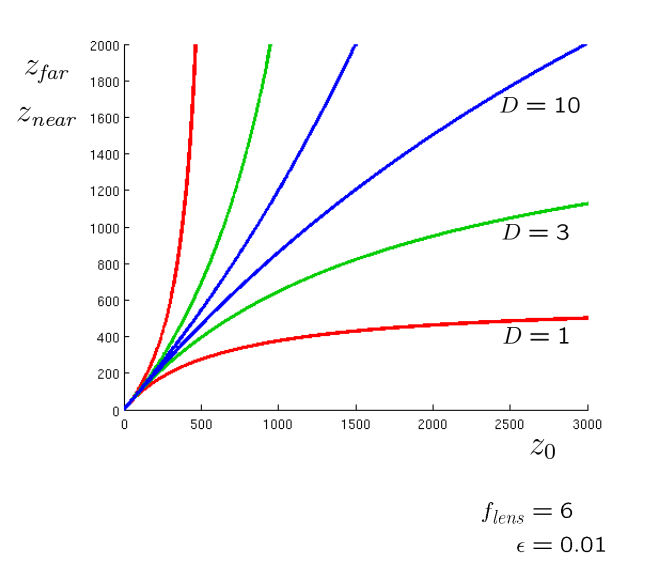
对焦
对焦包围/对焦堆叠图像系列具有不同的镜头和图像平面之间的距离,以克服有限的景深
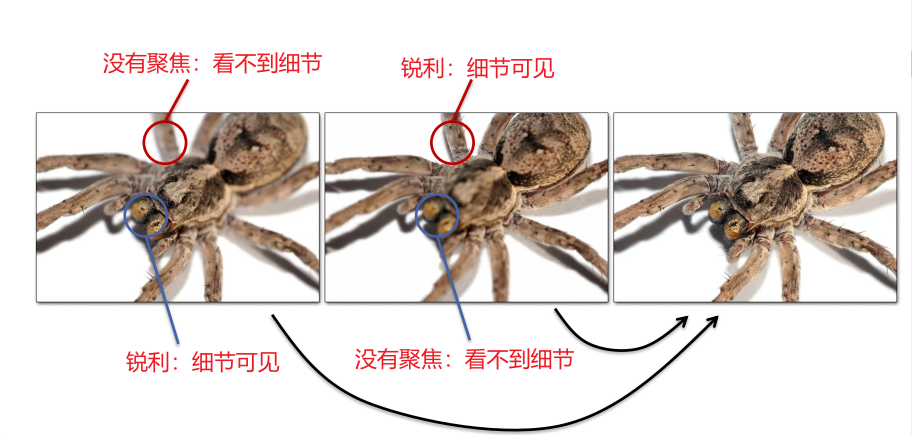
像差 Lens Aberrations
-
几何像差:由于镜头几何形状不完善,没有唯一焦点
– 球面像差、散光、彗差
geometric aberrations: no unique focal point due to imperfect lens geometry – spherical aberration, astigmatism, coma
-
色差:因不同波长的不同折射率引起的色散(“彩虹效应”)
chromatic aberrations: dispersion caused by different refraction index for different wavelength (“rainbow effect”)
- 渐晕:图像周边的光强度和饱和度降低
vignetting: reduced light intensity and saturation in the image periphery
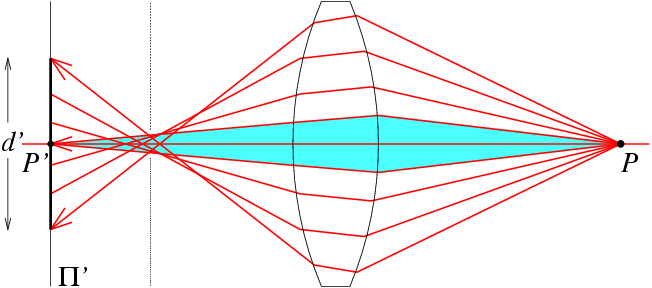

图象失真
图像失真:透视投影应将线映射到线。
但大多数相机不会 → 畸变
– 径向畸变 镜头形状欠佳
– 切向畸变 镜头安装欠佳

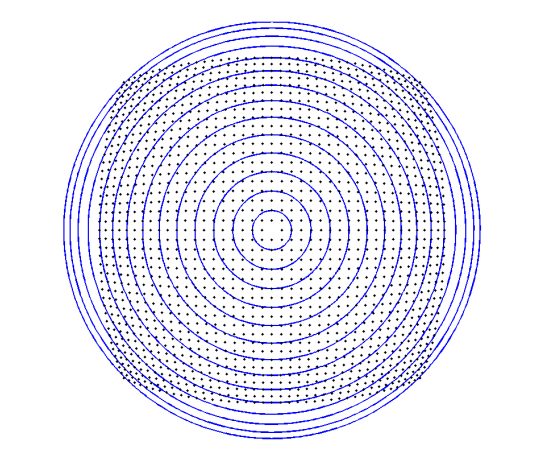
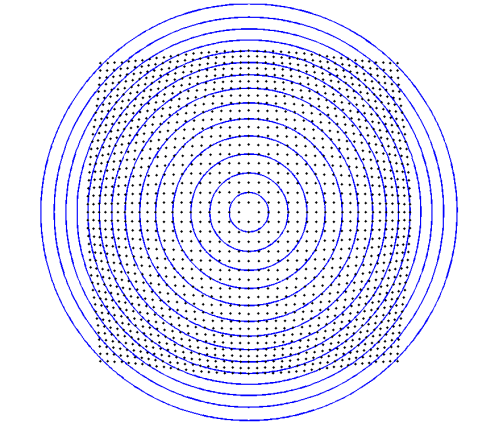
径向畸变
- 点偏离主点
- 径向畸变是对称的
- 偏移量与到主点的距离呈非线性关系
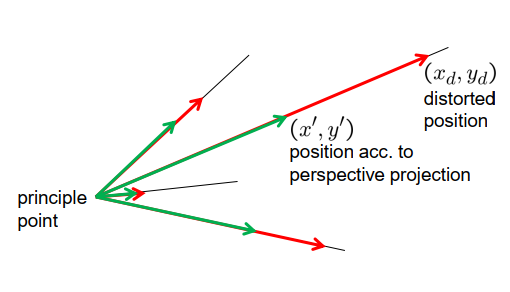
- 矩形对象在图像中呈桶形或枕形
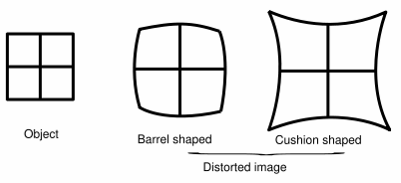
偶数多项式的数学建模:
\[\left(\begin{array}{l}x^{\prime} \\ y^{\prime}\end{array}\right)=\left(1+k_{1} r^{2}+k_{2} r^{4}\right)\left(\begin{array}{l}x_{d} \\ y_{d}\end{array}\right) \quad \text{ with } r^{2}=x_{d}^{2}+y_{d}^{2}\]或在图像坐标中:
\[\left(\begin{array}{l}u^{\prime} \\ v^{\prime}\end{array}\right)=\left(\begin{array}{l}u_{0} \\ v_{0}\end{array}\right)+\left(1+k_{1} r^{2}+k_{2} r^{4}\right)\left(\begin{array}{l}u_{d}-u_{0} \\ v_{d}-v_{0}\end{array}\right) \text{with } r^{2}=\left(u_{d}-u_{0}\right)^{2}+\left(v_{d}-v_{0}\right)^{2}\]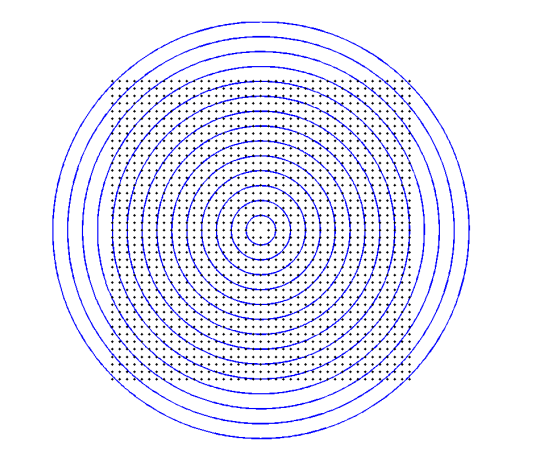


相机标定 Camera Calibration
常用术语 内参矩阵: Intrinsic Matrix 焦距: Focal Length 主点: Principal Point 径向畸变: Radial Distortion 切向畸变: Tangential Distortion 旋转矩阵: Rotation Matrices 平移向量: Translation Vectors 平均重投影误差: Mean Reprojection Error 重投影误差: Reprojection Errors 重投影点: Reprojected Points ———————————————— 版权声明:本文为CSDN博主「AI人工智能科学」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/lql0716/article/details/71973318
建立相机成像几何模型并矫正透镜畸变。
参数:
-
内在参数:描述相机(5个参数)
\[u_{0}, v_{0}, \alpha^{\prime}, \beta^{\prime}, \theta\] -
外部参数:相机的位姿(2个参数)
\[R,\vec{t}\]失真参数:
\[k_1,k_2\]
校准 = 确定参数的过程
校准:从成对的图像点和世界点确定相机参数
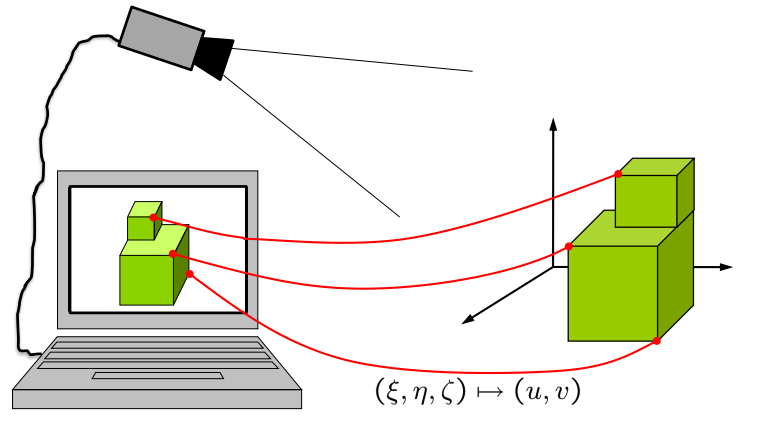
从一张或几张图片我们得到对应的点:
\[\left(\xi_{i}, \eta_{i}, \zeta_{i}\right) \mapsto\left(u_{i}, v_{i}\right)\]找到映射 \(\left(\xi_{i}, \eta_{i}, \zeta_{i}\right)\) 到尽可能好的相机参数 \(A,R,\vec{t}\) 在 \(\left(u_{i}, v_{i}\right)\)
几种方法。 这里: 1. Tasi的方法 2. 张氏方法
世界到图像映射:
\[z \cdot\left(\begin{array}{l}u \\ v \\ 1\end{array}\right)=\underbrace{A \cdot(R \mid \vec{t})}_{=: M} \cdot\left(\begin{array}{l}\xi \\ \eta \\ \zeta \\ 1\end{array}\right)\]M 是 3x4 矩阵
\[M=\left(\begin{array}{ccc}m_{1,1} & \ldots & m_{1,4} \\ \vdots & \ddots & \vdots \\ m_{3,1} & \ldots & m_{3,4}\end{array}\right)\]我们得到:
\[\vec{m}_{1,1: 3}\left(\begin{array}{l}\xi \\ \eta \\ \zeta\end{array}\right)+m_{1,4}-u\left(\vec{m}_{3,1: 3}\left(\begin{array}{l}\xi \\ \eta \\ \zeta\end{array}\right)+m_{3,4}\right)=0\] \[\vec{m}_{2,1: 3}\left(\begin{array}{l}\xi \\ \eta \\ \zeta\end{array}\right)+m_{2,4}-v\left(\vec{m}_{3,1: 3}\left(\begin{array}{l}\xi \\ \eta \\ \zeta\end{array}\right)+m_{3,4}\right)=0\]通过最小化确定相机参数
\[\sum_{i}\left(\left(\vec{m}_{1,1: 3}\left(\begin{array}{c}\xi_{i} \\ \eta_{i} \\ \zeta_{i}\end{array}\right)+m_{1,4}-u_{i}\left(\vec{m}_{3,1: 3}\left(\begin{array}{c}\xi_{i} \\ \eta_{i} \\ \zeta_{i}\end{array}\right)+m_{3,4}\right)\right)^{2}\right.\left.+\left(\vec{m}_{2,1: 3}\left(\begin{array}{c}\xi_{i} \\ \eta_{i} \\ \zeta_{i}\end{array}\right)+m_{2,4}-v_{i}\left(\vec{m}_{3,1: 3}\left(\begin{array}{c}\xi_{i} \\ \eta_{i} \\ \zeta_{i}\end{array}\right)+m_{3,4}\right)\right)^{2}\right)\]归零偏导数:
\(\left(\begin{array}{ccc}\sum_{i} S_{i} & 0 & -\sum_{i} u_{i} S_{i} \\0 & \sum_{i} S_{i} & -\sum_{i} v_{i} S_{i} \\-\sum_{i} u_{i} S_{i} & -\sum_{i} v_{i} S_{i} & \sum_{i}\left(u_{i}^{2}+v_{i}^{2}\right) S_{i}\end{array}\right) \cdot\left(\begin{array}{l}\vec{m}_{1,1: 4}^{T} \\\vec{m}_{2,1: 4}^{T} \\\vec{m}_{3,1: 4}^{T}\end{array}\right)=\overrightarrow{0}\) with \(S_{i}=\left(\xi_{i}, \eta_{i}, \zeta_{i}, 1\right)^{T}\left(\xi_{i}, \eta_{i}, \zeta_{i}, 1\right)\)
解:关于最小特征值的特征向量
- 1 个自由度:解的长度
解的结构:
\(M=A \cdot(R \mid \vec{t})=\left(\begin{array}{ll}\vec{m}_{1,1: 3} & m_{1,4} \\\vec{m}_{2,1: 3} & m_{2,4} \\\vec{m}_{3,1: 3} & m_{3,4}\end{array}\right)\) with \(\vec{m}_{1,1: 3}=\alpha^{\prime} \vec{r}_{1,1: 3}-\beta^{\prime} \cot \theta \vec{r}_{2,1: 3}+u_{0} \vec{r}_{3,1: 3}\) \(\begin{aligned}m_{1,4} &=\alpha^{\prime} t_{1}-\beta^{\prime} \cot \theta t_{2}+u_{0} t_{3} \\\vec{m}_{2,1: 3} &=\frac{\beta^{\prime}}{\sin \theta} \vec{r}_{2,1: 3}+v_{0} \vec{r}_{3,1: 3} \\m_{2,4} &=\frac{\beta^{\prime}}{\sin \theta} t_{2}+v_{0} t_{3} \\\vec{m}_{3,1: 3} &=\vec{r}_{3,1: 3} \\m_{3,4} &=t_{3}\end{aligned}\)
R 是一个旋转矩阵:
\[\left\|\vec{r}_{1,1: 3}\right\|=1 \\ \| \vec{r}_{2,1: 3} \|=1 \\\| \vec{r}_{3,1: 3}\|=1\\\left\langle\vec{r}_{1,1: 3}, \vec{r}_{2,1: 3}\right\rangle=0 \left\langle\vec{r}_{2,1: 3,}, \vec{r}_{3,1: 3}\right\rangle=0 \left\langle\vec{r}_{3,1: 3,}, \vec{r}_{1,1: 3}\right\rangle=0\]由于 \(\vec{m}_{3,1: 3}=\vec{r}_{3,1: 3}\) 选择解决方案 \(\left|\vec{m}_{3,1: 3}\right|^{2}=1\) (两种可能性,检查 \(\operatorname{det}(R)=+1)\)
给定 M,我们如何推导出相机参数 R, t, α’, β’, θ, u0, v0 ?

总结:Tsai 的方法
- 用校准标记(一般位置的标记)创建一个人工场景
- 测量校准标记的 3d 世界位置
- 制作图片
- 测量校准标记的 2d 图像位置
- 解决优化问题 估计矩阵 M
- 将 M 分解为 A, R, t
相机校准:张 Camera Calibration: Zhang
假设平面上的 3d-点\(\zeta=0\)
这些点由相机映射到
\(\begin{aligned}
z \cdot\left(\begin{array}{l}
u \\
v \\
1
\end{array}\right) &=A \cdot\left(R \cdot\left(\begin{array}{l}
\xi \\
\eta \\
0
\end{array}\right)+\vec{t}\right) \\
&=\underbrace{A \cdot\left(\vec{r}_{1: 3,1}, \vec{r}_{1: 3,2}, \vec{t}\right)}_{=: H} \cdot\left(\begin{array}{l}
\xi \\
\eta \\
1
\end{array}\right)
\end{aligned}\)
H 称为单应性 H is called a homography
\(H=A \cdot\left(\vec{r}_{1: 3,1}, \vec{r}_{1: 3,2}, \vec{t}\right)\)
如果我们知道几个单应性$H_1,H_2…H_n$,我们能推导出来$A$吗?让我们首先考虑
\(B=A^{-T} A^{-1}\)
A是满秩的,上三角矩阵
→ \(A^{-1}\) 存在并且也是上三角矩阵
→ B是对称的,有 6 个不同的条目
→ \(A^{-1}\) 可以通过 Cholesky 分解计算
→ 如果我们知道B,我们可以很容易地推导出 \(B=\left(\begin{array}{lll} b_{1,1} & b_{1,2} & b_{1,3} \\ b_{1,2} & b_{2,2} & b_{2,3} \\ b_{1,3} & b_{2,3} & b_{3,3} \end{array}\right)\)
\[H=A \cdot\left(\vec{r}_{1: 3,1}, \vec{r}_{1: 3,2}, \vec{t}\right)\]R是一个旋转矩阵,因此
(1) \(\begin{aligned} 0=\left\langle\vec{r}_{1: 3,1}, \vec{r}_{1: 3,2}\right\rangle &=\left\langle A^{-1} \vec{h}_{1: 3,1}, A^{-1} \vec{h}_{1: 3,2}\right\rangle \\ &=\vec{h}_{1: 3,1}^{T} \cdot\left(A^{-T} A^{-1}\right) \cdot \vec{h}_{1: 3,2} \\ &=\vec{h}_{1: 3,1}^{T} \cdot B \cdot \vec{h}_{1: 3,2} \end{aligned}\)
(2) \(\begin{aligned} \left\langle\vec{r}_{1: 3,1}, \vec{r}_{1: 3,1}\right\rangle=1=&\left\langle\vec{r}_{1: 3,2}, \vec{r}_{1: 3,2}\right\rangle \\ \left\langle A^{-1} \vec{h}_{1: 3,1}, A^{-1} \vec{h}_{1: 3,1}\right\rangle &\left\langle A^{-1} \vec{h}_{1: 3,2}, A^{-1} \vec{h}_{1: 3,2}\right\rangle \\ \vec{h}_{1: 3,1}^{T} \cdot B \cdot \vec{h}_{1: 3,1} & \vec{h}_{1: 3,2}^{T} \cdot B \cdot \vec{h}_{1: 3,2} \\ \Rightarrow 0=\vec{h}_{1: 3,1}^{T} \cdot B \cdot \vec{h}_{1: 3,1}-\vec{h}_{1: 3,2}^{T} \cdot B \cdot \vec{h}_{1: 3,2} \end{aligned}\) 因此,从一个单应性我们得到两个约束(1),(2)
如果我们知道几个单应性,我们能推导出来A吗?
- 从每个单应性我们得到两个约束
- 3 个单应性产生总共 6 个约束以估计 6 个参数
- 3 个单应性产生一个超定的约束系统
→ 最小二乘法找到一个使残差最小化的矩阵
概述:张的方法
-
…
-
…
-
…
-
估计单应性 H
-
求解优化问题以估计矩阵 B
-
将 B 分解为 A, R, t
-
…
我们如何得到单应性?
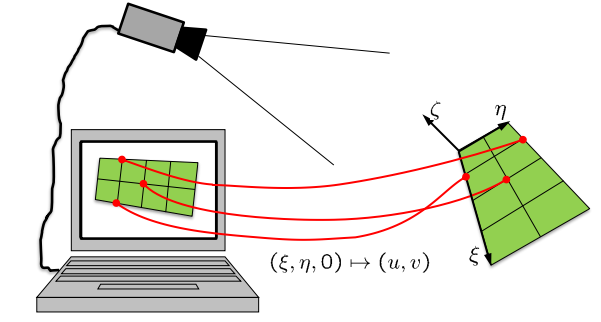
-
假设平面上点的一组点对应关系
-
找到单应性使得
- 一个对应产生两个约束
- 最小二乘以最小化残差并找到最佳单应性H
概述:张的方法
- 在已知位置创建一个带有校准标记的平面
- 制作几张平面不同位置和方向的图片
- 测量标记的二维图像位置
- 估计每张图片的单应性 H
- 求解 估计矩阵 B 的优化问题
- 将 B 分解为 A, R, t
- 使用非线性最小二乘法优化所有参数
最后,我们得到
- 内在参数 A
- 每个平面的旋转 R 和平移 t
校准失真参数 k1、k2:
– 非线性优化过程
– 内在、外在参数和失真参数的迭代估计
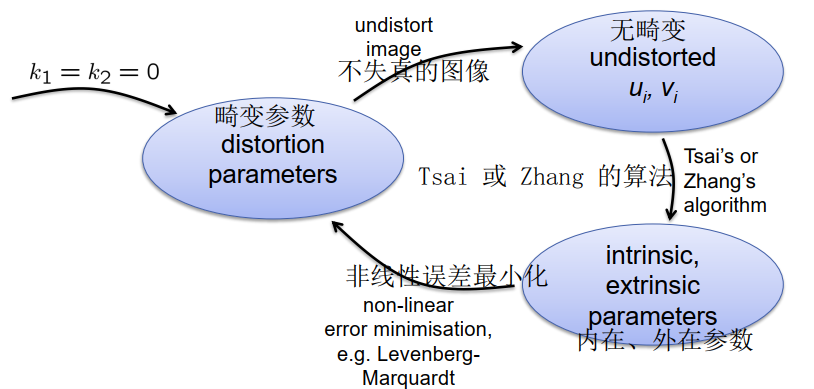
无畸变的效果图

不失真(需要更复杂的失真模型):

校准指示器:
- 性能特点
- 清晰可识别
- 易于确定世界位置
- 易于在图像中高精度定位
- 世界上不共面的特征(对于 Tsai 的方法)
- 避免遮挡
- 避免阴影
- 尽可能多
棋盘标记
确定图像位置,计算水平和垂直边缘的交点

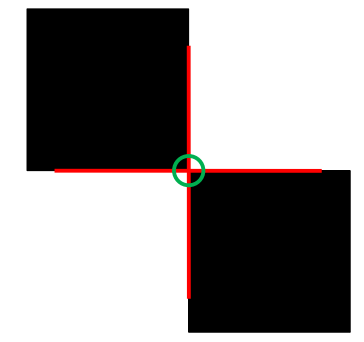
正方形和矩形 - 确定图像位置,计算水平和垂直边缘的交点

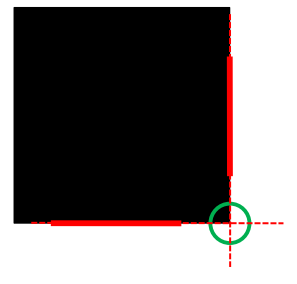
圆 确定结果椭圆的中心 - 圆心映射误差的迭代校正
非标相机
远心镜头 Telecentric Lenses
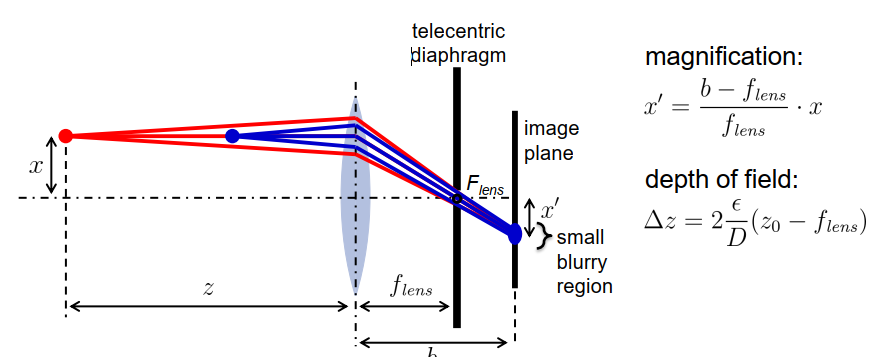
优点:– 放大倍率与物距无关 – 改善景深
缺点:– 小光圈,让光线很差 – 大、重且昂贵
应用领域:显微镜

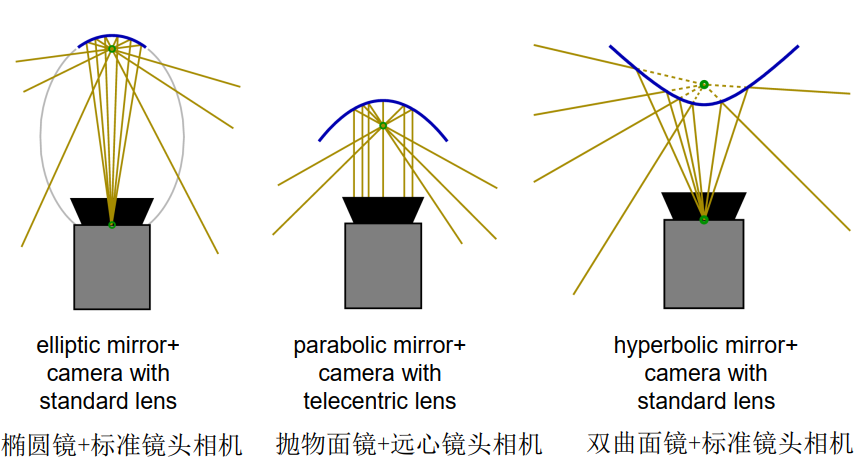
折反射相机 = 带镜子的相机
平面镜
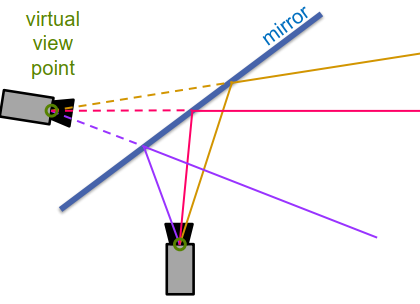
– 曲面镜
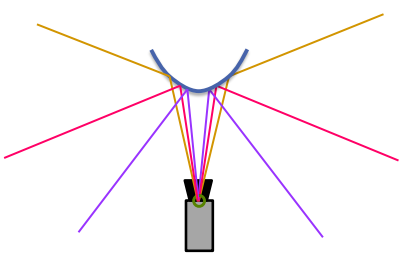
折反射相机
单视点
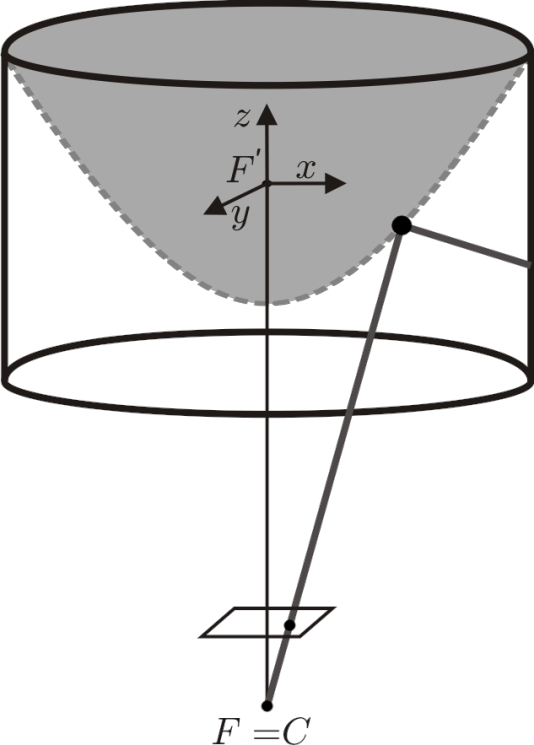
如果所有物镜光线都在一个点相交(例如,如果镜子可以用针孔相机代替),则折反射相机具有单一视点
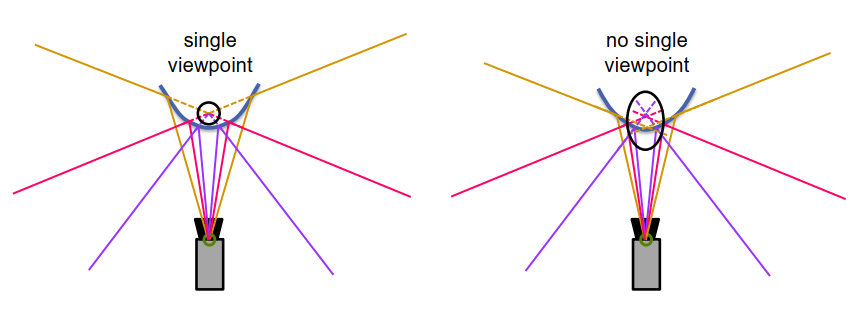
单视点相机设置: