曲线拟合——圆和椭圆

在上一篇文章中，我们总结了视觉识别中对于直线型边缘的拟合。但是如果有的图形边缘是曲线的话应该怎么拟合？ 这一篇博文，我们就对其进行讨论。

标准圆

首先圆的方程为：\(\left(x-m_{1}\right)^{2}+\left(y-m_{2}\right)^{2}-r^{2} = 0\)

因为d很小，用趋近的想法来考虑

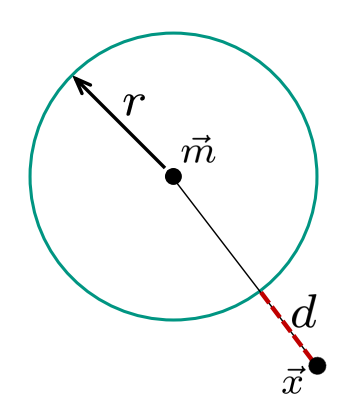
那么点(x,y)到圆的欧几里得距离大小为：

代数距离为

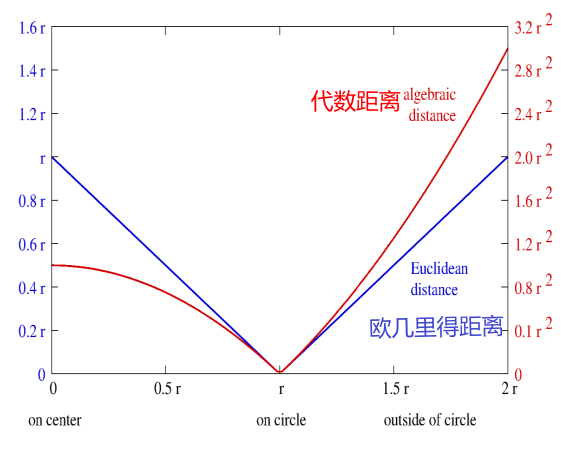
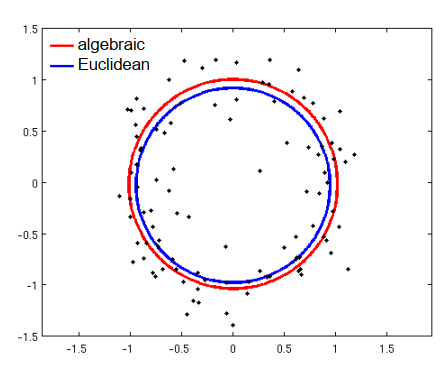
根据图知道，欧几里得距离和代数距离是不对称的，靠近圆的点都是相似的。

两种思路：最小化欧几里得距离和最小化代数距离。解析法

1. 最小化欧几里得距离 不能用解析法求解，必须数值优化

   解析法又称为分析法，它是应用解析式去求解数学模型的方法。 数学中用解析式表示函数或任意数学对象的方法叫解析法。

2. 最小化代数距离

   1. 重写代数距离：\(\begin{aligned} \left(x-m_{1}\right)^{2}+\left(y-m_{2}\right)^{2}-r^{2} &=\left(x^{2}+y^{2}\right)+\left(m_{1}^{2}+m_{2}^{2}-r^{2}\right)+\left(-2 m_{1}\right) x+\left(-2 m_{2}\right) y \\ &=A x+B y+C+\left(x^{2}+y^{2}\right) \\ \text { with } & A=-2 m_{1}, B=-2 m_{2}, C=m_{1}^{2}+m_{2}^{2}-r^{2} \end{aligned}\)
   2. 最小化：\(\sum_{i=1}^{N}\left(A x_{i}+B y_{i}+C+\left(x_{i}^{2}+y_{i}^{2}\right)\right)^{2}\)
   3. 偏导数归零: \(\left(\begin{array}{ccc} \sum_{i} x_{i}^{2} & \sum_{i} x_{i} y_{i} & \sum_{i} x_{i} \\ \sum_{i} x_{i} y_{i} & \sum_{i} y_{i}^{2} & \sum_{i} y_{i} \\ \sum_{i} x_{i} & \sum_{i} y_{i} & N \end{array}\right)\left(\begin{array}{l} A \\ B \\ C \end{array}\right)=\left(\begin{array}{c} -\sum_{i} x_{i}\left(x_{i}^{2}+y_{i}^{2}\right) \\ -\sum_{i} y_{i}\left(x_{i}^{2}+y_{i}^{2}\right) \\ -\sum_{i}\left(x_{i}^{2}+y_{i}^{2}\right) \end{array}\right)\)
   4. 最后得到： \(\begin{aligned} m_{1} &=-\frac{A}{2} \\ m_{2} &=-\frac{B}{2} \\ r^{2} &=m_{1}^{2}+m_{2}^{2}-C \end{aligned}\)

椭圆

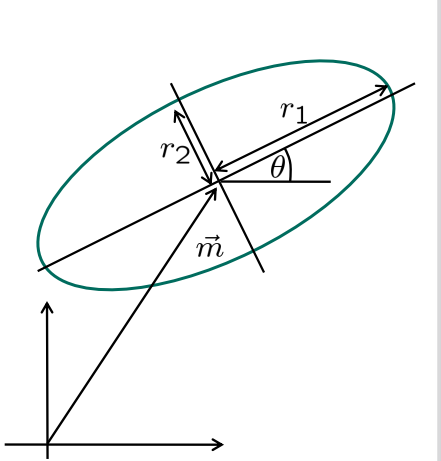
椭圆特性：

长短轴：半长轴r1，半短轴r2；

中心点：m

旋转角：θ

代数表达式：\(\begin{array}{l} A x^{2}+H x y+B y^{2}+G x+F y+C=0 \\ \text { with } 4 A B-H^{2}>0 \end{array}\)

当消除一个自由度时：\(\begin{array}{l} A=1 \\ \text { or } A+B=1 \\ \text { or } A^{2}+B^{2}+C^{2}+F^{2}+G^{2}+H^{2}=1 \\ \text { or } C=1 \text { (not invariant to translation) } \end{array}\)

根据椭圆的特性，Fitzgibbon, Pilu, 和 Fisher在1999年提出了基于直接最小二乘的椭圆拟合算法，

最小化了代数距离(通过最小化的约束条件: \(4 A B-H^{2}=1\))