曲线拟合 Curve Fitting
在上一篇文章中,我们讨论了图像的边缘检测,但是边缘检测完毕后存在一个问题就是噪点多,或者换句话说不光滑。
所以我们再增加一个步骤来使得图像轮廓更加平滑:曲线拟合。
原始图像–>(通过边缘检测)得到边缘图像–>(通过轮廓探测contour detector)得到坐标值(几何描述)
在进行正式的拟合之前,我们先回顾一下二维几何知识:向量
向量
向量知识中有个很重要的概念:点积。点积的意义主要是表征向量的相似性。值越大代表相似性越好。
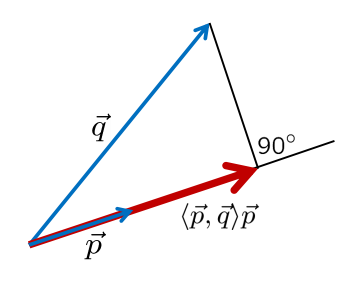
- 定义:$\langle\vec{p}, \vec{q}\rangle=p_{1} q_{1}+p_{2} q_{2}$ 其中p=(p1,p2), q=(q1,q2)
- 双线性:$\langle\alpha \vec{p}+\beta \vec{r}, \gamma \vec{q}+\delta \vec{s}\rangle=\alpha \gamma\langle\vec{p}, \vec{q}\rangle+\alpha \delta\langle\vec{p}, \vec{s}\rangle+\beta \gamma\langle\vec{r}, \vec{q}\rangle+\beta \delta\langle\vec{r}, \vec{s}\rangle$
- 几何定义:$\langle\vec{p}, \vec{q}\rangle=|\vec{p}| \cdot|\vec{q}| \cdot \cos \angle(\vec{p}, \vec{q})$
- 拓展:
$\langle\vec{p}, \vec{p}\rangle=|\vec{p}|^{2}$, $\langle\vec{p}, \vec{q}\rangle=0 \quad$ if $\vec{p} \perp \vec{q}$
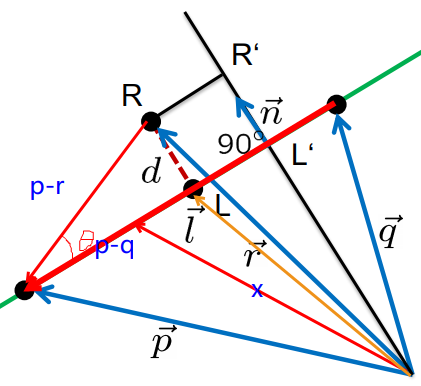
- 线和线段
我们可以把任意向量$\vec{x}$表示为$\vec{p}-\vec{q}$的某一段,我们用$\tau$表示比例,即$\tau(\vec{p}-\vec{q})$, $\tau \in[0,1]$
那么我们可以得到$\vec{x}=\vec{p}+\tau(\vec{p}-\vec{q})$
化简得到:
$\vec{x}=(1-\tau) \vec{p}+\tau \vec{q}, \quad \tau \in[0,1]$
同理:$\vec{l}$也可通过以上表达:$\vec{l}=(1-\tau) \vec{p}+\tau \vec{q}, \quad \tau \in[0,1]$
$\vec{l}-\vec{r}=d代表的向量$
$<\vec{l}-\vec{r},\vec{p}-\vec{q}>=0$ 说明d和直线垂直
-
直线的一般形式:
$|\vec{n}|=1,\langle\vec{n}, \vec{q}-\vec{p}\rangle=0$ ,$|\vec{n}|为单位向量$
$\langle\vec{n}, \vec{x}\rangle=\langle\vec{n},(1-\tau) \vec{p}+\tau \vec{q}\rangle=\langle\vec{n}, \vec{p}\rangle+\tau\langle\vec{n}, \vec{q}-\vec{p}\rangle=\langle\vec{n}, \vec{p}\rangle$
$\begin{aligned} 0 &=\langle\vec{n}, \vec{x}\rangle-\langle\vec{n}, \vec{p}\rangle \ &=\langle\vec{n}, \vec{x}\rangle+c \quad \text { (normal form) } \end{aligned}$
-
点到直线的距离d:
\[d=|| \vec{l}-\vec{r} \|=|\langle\vec{n}, \vec{r}\rangle+c|\]
用单位向量表示一般向量:
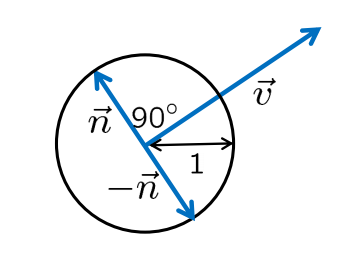
$\vec{v}=\left(\begin{array}{l}v_{1} \ v_{2}\end{array}\right)$
$\vec{n}=\frac{1}{|\vec{v}|}\left(\begin{array}{c}-v_{2} \ v_{1}\end{array}\right)$
$\rightarrow \quad|\vec{n}|=1, \vec{n} \perp \vec{v}$
每个向量都可以用极坐标来表示:
\[\vec{v}=r \cdot\left(\begin{array}{c}\cos \phi \\ \sin \phi\end{array}\right) \quad,r \geq 0, \phi \in[0,2 \pi)\] \[\phi=\operatorname{atan}_{2}\left(v_{1}, v_{2}\right)\]通过点积可以来判断一个多边形是否面向摄像机(游戏开发中重要的一点);根据点积来计算光照效果(聚光);在计算机图学中进行方向性的判断
霍夫转换 Hough Transform
在边缘检测完毕后,我们通过霍夫转换,可以在边缘位图(edge bitmaps)中找到边缘线,每条线可以通过下面的式子来代替:
$x \cdot \cos \phi+y \cdot \sin \phi+c=0$
with $0^{\circ} \leq \phi<180^{\circ}$ and $c \in \mathbb{R}$
为什么可以这么表示呢?
因为在一般笛卡尔坐标系的直线表达式中,如y = kx+b,存在斜率为无穷大的情况,我们想办法找到一个类似于极坐标的表达方式。通过以上公式表达的方式我们称之为参数空间。在笛卡尔坐标系中的直线表达和 参数空间内的直线表达可以理解为一种映射,可以理解为同一种物体的不同维度的观察。
我们知道图中直线和它的垂线(虚线),一旦直线位置确定,那么其垂线的位置也是确定的。反之亦然。
如何找到这种映射关系呢?
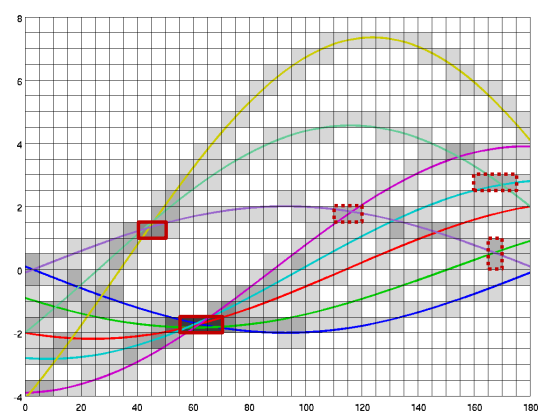
假设有三个点A,B,C我们要判断其是否共线,这里我们假设其共线。

这条线的方程为
\[y=-x+2\]围绕A点可以做无数条直线,B、C同理。那么如果说其中的某三条线重合了,说明ABC共线。
那么这三条线的极坐标表示也是一样的,在参数空间内就相交于一点。
那么围绕A点扫描的所有直线的表达式为:
\[f=0 \times \sin \theta+2 \times \cos \theta, \theta \in[0, \pi]\]围绕B点扫描的所有直线表达式为:
\[f=2 \times \sin \theta+0 \times \cos \theta, \theta \in[0, \pi]\]围绕C点扫描的所有直线表达式为:
\[f=4 \times \sin \theta-2 \times \cos \theta, \theta \in[0, \pi]\]然后做出函数图像,我们发现,三个函数交于
\[\left(\frac{\pi}{4}, \sqrt{2}\right)\]我们现在知道了,他们相交的直线是以辐角为45°,幅值为$\sqrt{2}$的直线,大家再看笛卡尔坐标系中的直线位置,就明白了其映射关系。大家可以使用其他值作为例子进行体会。

霍夫转换的基本步骤
- 根据边缘线在参考空间中计算或者画出正弦曲线
- 计算交点
值得注意的是,在现实图像处理中,交点并不唯一。(多条线混合在一起)
所以我们只能在高密度的区域中进行找点:
- 使用离散累加器单元阵列;
- 对每个单元计算正弦曲线穿过的数量;
- 在累加器阵列中进行局部最大值处理(根据线的参数)
有点类似我们小时候画三角形的垂直平分线,画完后交不到一点,我们用铅笔继续涂黑。
在许多边缘上的许多边缘点的霍夫变换
- 用0初始化具有足够精度的累加器阵列
- 使得所有满足线方程的累加器单元增加计数(有点拗口,就是计数)
- 在累加器中找到局部最大值(图像中最主要的参数)
在找到线参数后,可以将离线距离小的边缘像素分配到边缘线上。
但需要做两个工作:1. 确定线的起点和终点。2. 确定允许最大尺寸的间隙。
霍夫变换的性质
- 结果取决于累积器数组的大小和精度
- 在实践中,确定累积器阵列中的重要峰值可能是困难的
- 梯度方向被忽略
- 累加器数组在”自然场景“中溢出(我猜是计算量过大)
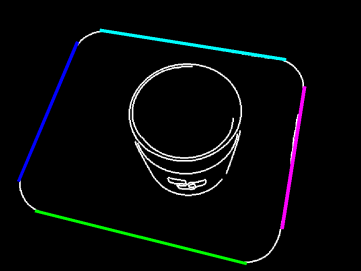
上图是一张经过霍夫变换后的图,在图中我们可以知道,圆弧部分并没有找到。
边缘追踪 Edge following
鉴于霍夫变换的缺点,我们可以通过另一条路线:
边缘检测edge detection–>边缘追踪edge following–>线段分割polyline segmentation–>直线拟合 line fitting
边缘追踪大体思路
- 边缘检测器产生具有边缘像素的位图
- 收集所有边缘像素并按拓扑顺序链接它们
- 使用梯度信息(如果可用)进行链接
- 结果:描述轮廓线的边缘像素列表
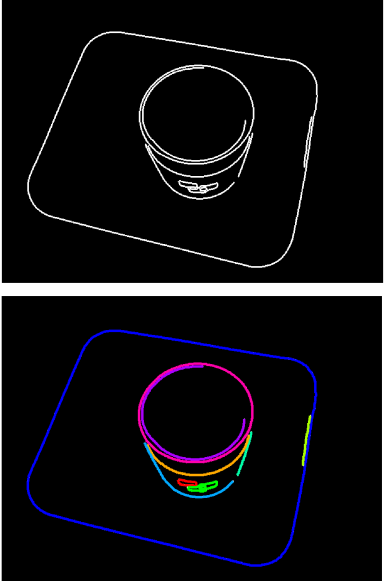
直线分割 Polyline Segmentation
边缘跟踪产生了有序的像素列表,但这些像素列表并不会主动或者自动的生成连线用以表示轮廓,所以我们的任务就是:细分像列表,使子列表可以用线段表示。
这里有很多的算法,我们只考虑Ramer Douglas Peucker算法,道格拉斯-普克算法
道格拉斯-普克算法的基本思路
在最远的顶点进行递归细分折线
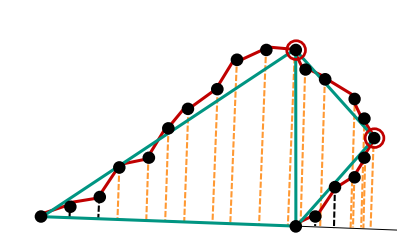
- 从第一个点到最后一个点连成线
- 计算各像素到线的距离
- 若最大的距离大于容差(自己定义的),则在最远的顶点打破边缘列表,并将算法再次应用到两个子列表(列表被打破成两个)
总体思想就是递归思想。
直线拟合
由于折线分割和霍夫转换的结果不一定是最优的,所以我们提出直线拟合的算法。
很容易想到我们以前中学学过的直线拟合算法:最小二乘法
最小二乘法
在这里我们做一下基本的回顾和加深:
在前面的二维几何知识回顾里,我们知道了:
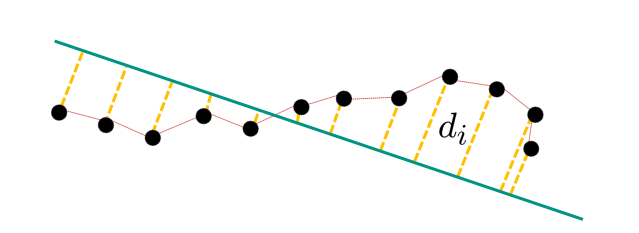
如果给定了我们单位向量$\vec{n}$以及$c$, 我们可以计算$\overrightarrow{x_{i}}$到直线的距离为
\[d_{i}=\left|\left\langle\vec{n}, \vec{x}_{i}\right\rangle+c\right|\]我们找到最小的$d_{i}$
不想看推到过程的可以跳到后面,看结论就行了。
完全最小二乘法:
\[\underset{\vec{n}, c}{\operatorname{minimise}} \sum_{i=1}^{N} d_{i}^{2}\] \[\text { subject to }\langle\vec{n}, \vec{n}\rangle=1\]拉格朗日算子(自行回顾高等数学)
\[\mathcal{L}(\vec{n}, c, \lambda)=\sum_{i=1}^{N} d_{i}^{2}-\lambda(\langle\vec{n}, \vec{n}\rangle-1)\] \[=\sum_{i=1}^{N}\left(\left\langle\vec{n}, \vec{x}_{i}\right\rangle+c\right)^{2}-\lambda(\langle\vec{n}, \vec{n}\rangle-1)\]对$c$进行归零偏导
\[\frac{\partial \mathcal{L}}{\partial c}=2 \sum_{i=1}^{N}\left\langle\vec{n}, \vec{x}_{i}\right\rangle+2 N c \stackrel{!}{=} 0\] \[\rightarrow c=-\frac{1}{N} \sum_{i=1}^{N}\left\langle\vec{n}, \vec{x}_{i}\right\rangle=-\frac{1}{N}\left\langle\vec{n}, \sum_{i=1}^{N} \vec{x}_{i}\right\rangle=-\left\langle\vec{n}, \frac{1}{N} \sum_{i=1}^{N} \vec{x}_{i}\right\rangle\]对$n_{1}$和$n_{2}$归零偏导
\[\frac{\partial \mathcal{L}}{\partial n_{1}}=2\left(\sum_{i} x_{i, 1}^{2}\right) n_{1}+2\left(\sum_{i} x_{i, 1} x_{i, 2}\right) n_{2}+2\left(\sum_{i} x_{i, 1}\right) c-2 \lambda n_{1} \stackrel{!}{=} 0\] \[\frac{\partial \mathcal{L}}{\partial n_{2}}=2\left(\sum_{i} x_{i, 1} x_{i, 2}\right) n_{1}+2\left(\sum_{i} x_{i, 2}^{2}\right) n_{2}+2\left(\sum_{i} x_{i, 2}\right) c-2 \lambda n_{2} \stackrel{!}{=} 0\]替换:
\[\underbrace{\left(\sum_{i} x_{i, 1}^{2}-\frac{1}{N}\left(\sum_{i} x_{i, 1}\right)^{2}\right)}_{=: \alpha} n_{1}+\underbrace{\left(\sum_{i} x_{i, 1} x_{i, 2}-\frac{1}{N} \sum_{i} x_{i, 1} \sum_{i} x_{i, 2}\right)}_{=: \beta} n_{2}=\lambda n_{1}\] \[\underbrace{\left(\sum_{i} x_{i, 1} x_{i, 2}-\frac{1}{N} \sum_{i} x_{i, 1} \sum_{i} x_{i, 2}\right)}_{=\beta} n_{1}+\underbrace{\left(\sum_{i} x_{i, 2}^{2}-\frac{1}{N}\left(\sum_{i} x_{i, 2}\right)^{2}\right) n_{2}=\lambda n_{2}}_{=\gamma}\]用矩阵形式表示:
\[\left(\begin{array}{ll} \alpha & \beta \\ \beta & \gamma \end{array}\right) \vec{n}=\lambda \vec{n}\]$\lambda$是特征值,$\vec{n}$是特征向量
两种结果:
\[\lambda_{1} \geq \lambda_{2} \geq 0\]$\lambda_{2}$–>最小距离, $\lambda_{1}$–>最大距离。
最小二乘法的步骤
-
从所有的边缘像素中计算: $\sum_{i} x_{i, 1}, \sum_{i} x_{i, 2}, \sum_{i} x_{i, 1}^{2}, \sum_{i} x_{i, 2}^{2}, \sum_{i} x_{i, 1} x_{i, 2}$
- 计算矩阵 $\left(\begin{array}{ll}\alpha & \beta \ \beta & \gamma\end{array}\right)$ 的特征向量和特征值,取较小的特征值
- 根据$\vec{n}$计算$c$
- 如果您对线段感兴趣,请根据投影在线上的边缘像素确定起点和终点。
直线估计
稳健性
稳健性是指在估计过程中,拟合过程中,对模型误差的不敏感性。
在最小二乘法中,如果出现异常值,那么拟合的直线很容易被带偏。
然而异常值在机器视觉中经常出现。
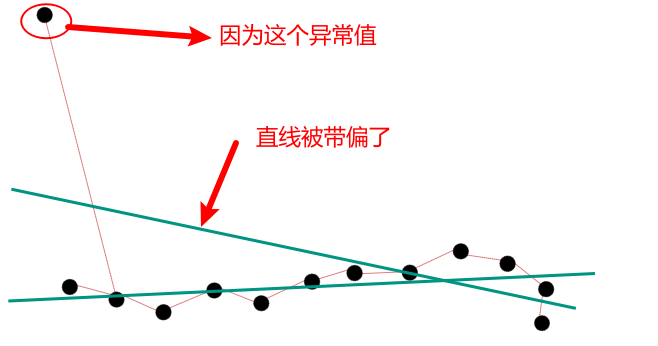
现在有两个思路:
- 减少总异常值的影响–> M估计,M Estimator
- 忽略异常值–>RANSAC算法
M估计
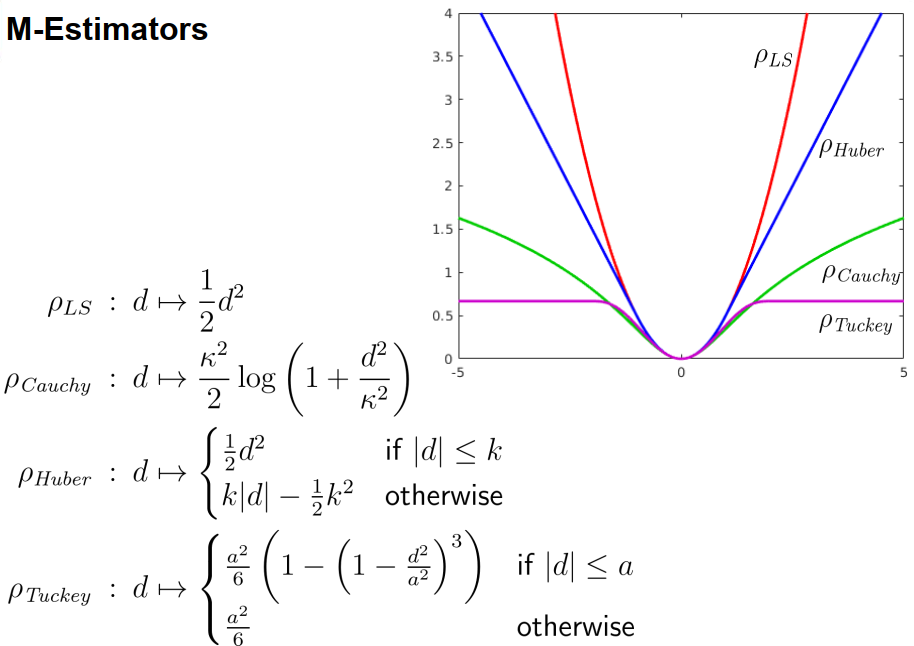
其中$\rho$越小,越靠近直线。
RANSAC随机抽样一致算法
一种通过使用观测到的数据点来估计数学模型参数的迭代方法
random sample consensus
RANSAC算法是一个学习的技巧,通过使用观测数据的随机样本来估计模型参数。RANSAC使用投票机制来寻找优化的拟合结果。每个数据元被用来投票一或多个模型。投票机制基于两点假设:
(1)噪音大的特征并不能一直单独为某个模型投票
(2)有足够多的特征来拟合一个好的模型
思路
搜索通过尽可能多点靠近的线
算法
- 随机选择两点
- 拟合
- 检查公差带之外的点数(异常值的数量)
- 用不同的点重复这个过程
- 选择异常值数量最少的线
