边缘检测的意义
边缘检测是为了提取图像中主体的轮廓特征.

灰度边缘的特性
- 在明亮和黑暗交接出有明显的改变(hard changes)
- 通常发生在物体的边缘处
- 发生在阴影和纹理处
- 边缘和亮度没有关系
- 人类的视觉皮层的许多部分都在处理灰度边缘
灰度:
把白色与黑色之间按对数关系分成若干级,成为灰度等级。范围一般从0-255,黑色为0.
寻找边缘
-
边缘是灰度变化最大的地方(其变化率最大,可以通过导数判断)
$g(u+\epsilon)-g(u-\epsilon)$
-
寻找区域内的g的导数的最大值
$\frac{\partial g}{\partial u}=\lim _{\epsilon \rightarrow 0} \frac{g(u+\epsilon)-g(u)}{\epsilon}=\lim _{\epsilon \rightarrow 0} \frac{g(u+\epsilon)-g(u-\epsilon)}{2 \epsilon}$
-
通过差分逼近函数进行近似(因为图片中为各个像素点,无法取极限,通过像素点之间的距离来代替)
$\frac{\partial g}{\partial u} \approx \frac{g(u+1)-g(u-1)}{2}$
-
近似导数可以实现为带滤波器掩码的卷积
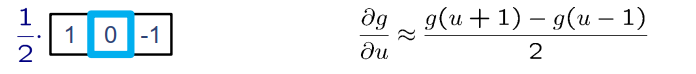
Prewitt算子,Sobel算子
Prewitt算子: 利用像素点上下,左右邻点的灰度差,在边缘处达到极值边缘检测
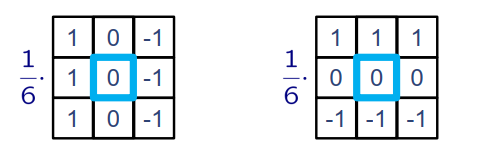
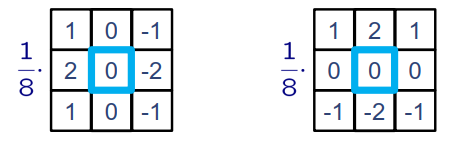
Sobel算子:与Prewitt算子相比,Sobel对像素的位置的影响做了加权,可以降低位置的影响
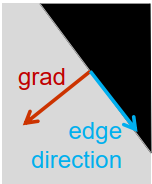
边缘方向
边缘方向edge direction:灰度梯度指向最大灰度上升的方向(正交方向没有灰度变化)
$\operatorname{grad} g=\left(\frac{\partial g}{\partial u}, \frac{\partial g}{\partial v}\right)$, $\operatorname{grad} g \perp\left(-\frac{\partial g}{\partial v}, \frac{\partial g}{\partial u}\right)$
Canny边缘检测
1. 高斯滤波
高斯滤波用于降噪,使图像变得平滑。
使用方法:用高斯矩阵乘以每个像素点及其邻域取其带权重的平均值作为最后的灰度值。
2. 使用边缘计算算子
上文中的Prewitt/Sobol算子
3. 使用非极大值抑制
非极大值抑制:搜索局部最大值,来抑制非极大值。例如在目标检测过程中,同一目标可能会出现大量候选框,我们通过非极大值抑制的方法来进行唯一化。
4. 使用双阈值法(上下阈值法)
使用一个阈值来检测边缘的效果不好,
小阈值:太多噪点,
大阈值:轮廓线连接不上。

二阶微分算子:Laplace算子
拉普拉斯算子属于最简单的各项同性二阶微分算子,对于二阶图像:
$\begin{aligned} \nabla^{2} g=& \frac{\partial^{2} g}{(\partial u)^{2}}+\frac{\partial^{2} g} {(\partial v)^{2}}\end{aligned}$
变化率最大处(一阶导数)=二阶导数为0
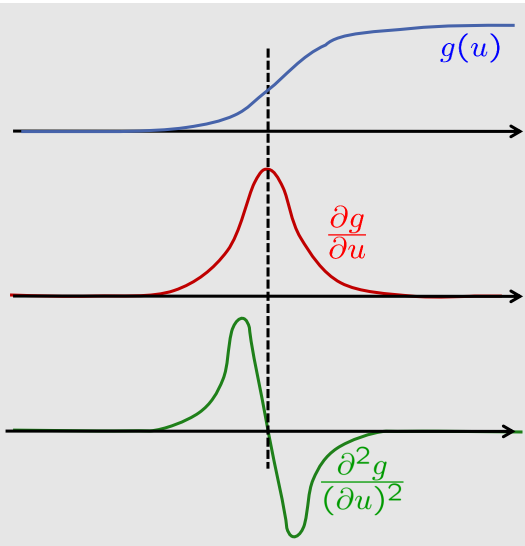
近似为拉普拉斯算子:
一阶导数:
$\frac{\partial g}{\partial u}(u, v) \approx g(u+1, v)-g(u, v)$
二阶导数:
$\begin{aligned} \frac{\partial^{2} g}{(\partial u)^{2}}(u, v) & \approx \frac{\partial g}{\partial u}(u, v)-\frac{\partial g}{\partial u}(u-1, v) \ & \approx g(u+1, v)-2 g(u, v)+g(u-1, v) \end{aligned}$
$ \frac{\partial^{2} g}{(\partial v)^{2}}(u, v) \approx g(u, v+1)-2 g(u, v)+g(u, v-1)$
可以得到:
$\nabla^{2} g \approx g(u+1, v)+g(u-1, v)+g(u, v+1)+g(u, v-1)-4 g(u, v)$
通过掩码器实现:
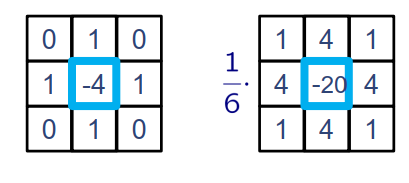
但是二阶导数带有很多的噪声,所以我们结合高斯平滑,从而形成高斯拉普拉斯算子
Laplacian of Gaussian, LoG
$\nabla^{2}(G * g)=\left(\nabla^{2} G\right) * g$ $(G$ Gaussian $)$ $G(u, v)=\frac{1}{2 \pi \sigma^{2}} e^{-\frac{1}{2 \sigma^{2}}\left(u^{2}+v^{2}\right)}$ $\begin{aligned} \frac{\partial G}{\partial u} &=\frac{1}{2 \pi \sigma^{2}}\left(-\frac{1}{2 \sigma^{2}}\right) 2 u e^{-\frac{1}{2 \sigma^{2}}\left(u^{2}+v^{2}\right)} \ &=-\frac{u}{\sigma^{2}} G(u, v) \ \frac{\partial^{2} G}{(\partial u)^{2}} &=-\frac{1}{\sigma^{2}} G(u, v)-\frac{u}{\sigma^{2}}\left(-\frac{u}{\sigma^{2}} G(u, v)\right) \ &=\frac{u^{2}-\sigma^{2}}{\sigma^{4}} G(u, v) \ \nabla^{2} G &=\frac{u^{2}+v^{2}-2 \sigma^{2}}{\sigma^{4}} G(u, v) \end{aligned}$
通过掩码器实现:
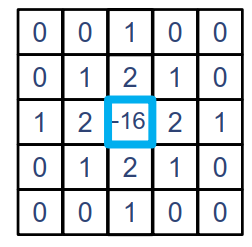
LoG算法可以近似为DoG算法:
$D o G(u, v)=G_{\sigma_{1}}(u, v)-G_{\sigma_{2}}(u, v)$
关于DoG的介绍:https://stonema.github.io/2018/04/16/LoG%E7%AE%97%E5%AD%90%E4%B8%8EDoG%E7%AE%97%E5%AD%90/
