图像预处理 Image Preprocessing
图像形成与分析
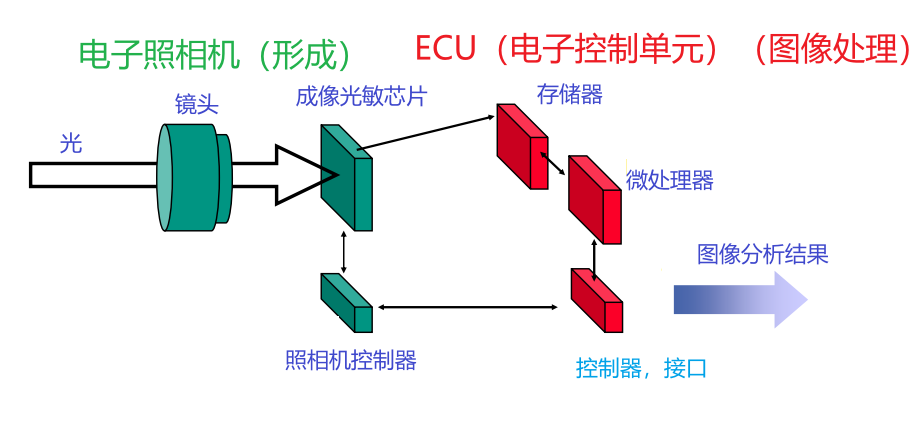
成像器
图像形成过程:
- 入射光强度
- 成像仪的输出
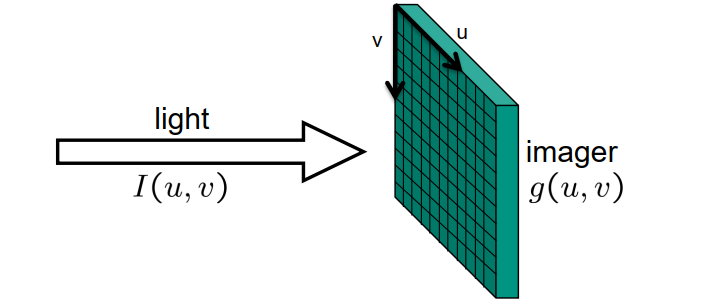
图像形成过程:
– 采样sampling
评估规则网格上的光强度
– 量化 quantization
将连续信号映射到离散值(自然数)
– 模糊和噪声 blur and noise
– 颜色将在后面讨论。 这里:只有光强度/灰度图像
采样
用于采样的二维网格

电子相机:矩形等距网格
生物:具有不同分辨率的六边形网格
波纹图案 Moiré Patterns
莫列波纹(英语:Moiré pattern),又译为摩尔纹、莫尔条纹、叠纹、水状波纹,是一种在栅栏状条纹重叠下所产生的干涉影像。莫列波纹来自法语:moiré,是一种纺织品,它的纹路类似于水波。最早这种纺织品是由丝作成,后来也用棉线或人造纤维来呈现相同的效果。
当感光元件像素的空间频率与影像中条纹的空间频率接近时,可能产生一种新的波浪形的干扰图案,即所谓的莫列波纹。
sampling might cause artifacts 采样可能会导致伪影

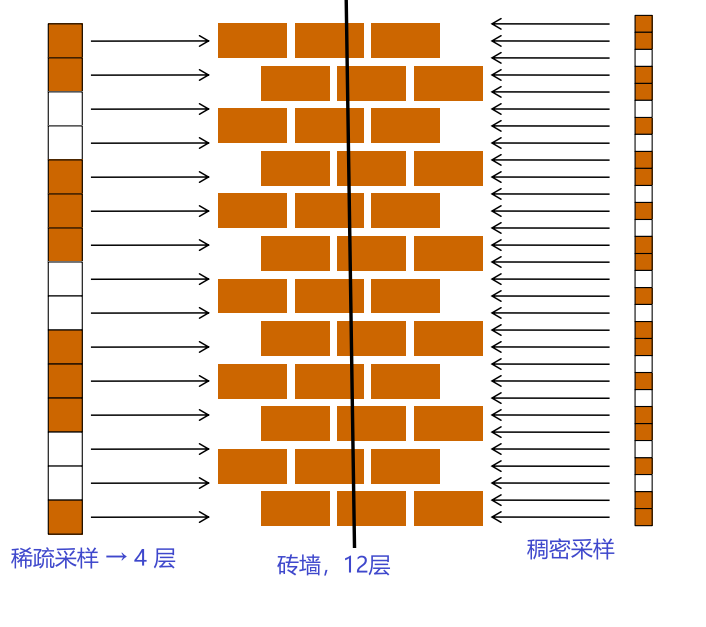
摩尔纹图案的一维示例:
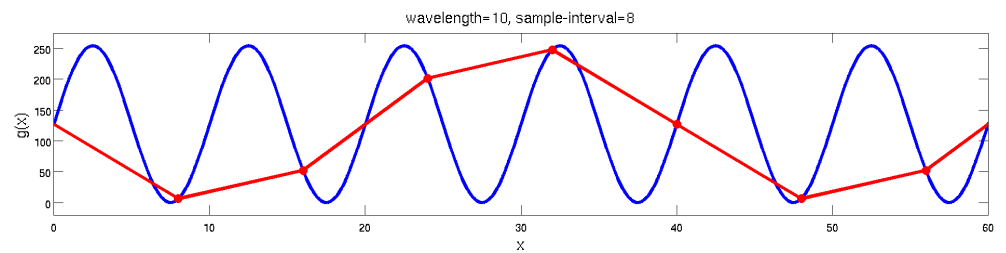
==莫尔条纹的出现取决于与信号最大频率相比的采样率(图像)==
The occurrence of Moiré patterns depends on the sampling rate compared to the maximal frequency of the signal (image)
香农采样定理
如果$f$是具有截止频率$k_0$的有界信号,那么它完全是通过在一系列最多$1/2k_0$间隔的点处给出其纵坐标来确定的,即 采样频率必须大于$2k_0$
- 什么是带界信号?
- 什么是截止频率?
傅里叶变换 Fourier Transform
假设一个周期信号
然后,我们可以定义傅里叶变换$f$
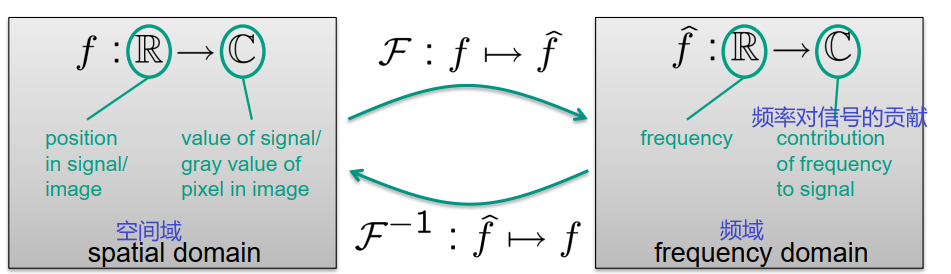
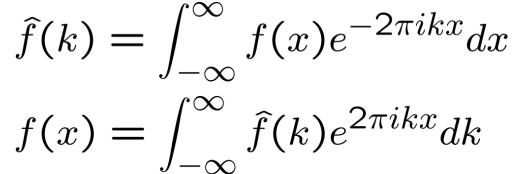
性质:
- 线性性质:
-
沿 x 轴移动信号只会改变频域中的复角,但不会改变幅度 shifting a signal along the x-axis only changes the complex angles in frequency domain but not the amplitudes
位移性质:
-
在空间域中重新缩放 x 轴以倒数方式重新缩放频率轴 rescaling the x-axis in the spatial domain rescales the frequency axis in a reciprocal way
比例变换性质
在空间域中重新缩放 x 轴以倒数方式重新缩放频率轴
– 空间域中的余弦在频域中产生两个峰值
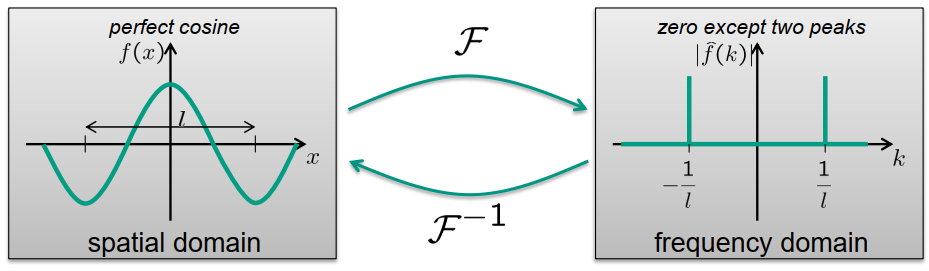
峰值位于周期长度的倒数位置
如果空间域中的信号是余弦的线性组合,则傅里叶变换将是频域中的一组峰值
直观的解释:傅里叶变换将周期信号分解为(可能是无限的)余弦的线性组合
观察
- 具有小斜率的平滑周期函数可以由具有大周期的余弦组成
- 具有大斜率的周期函数需要具有小周期的余弦
- 不连续或具有不连续导数的周期函数需要具有无限频率的余弦
定义:如果对于大于截止频率的所有频率,其傅里叶变换为零,则信号$f$以截止频率$k_0$为界,即
\[\widehat{f}(k)=0 \text { for all } k \text { with }|k| \geq k_{0}\]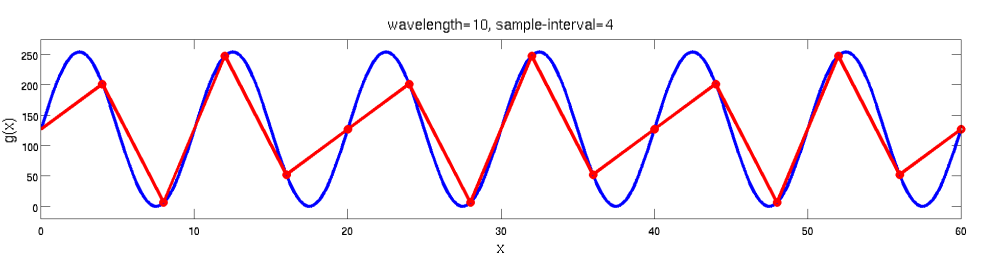
- 信号是带界的(正弦函数)
- 采样频率足够高
- 可以重建信号

图像缩放和插值 Image Scaling and Interpolation
- 改变图像大小
- 缩放需要在非整数位置评估图像 → 插值
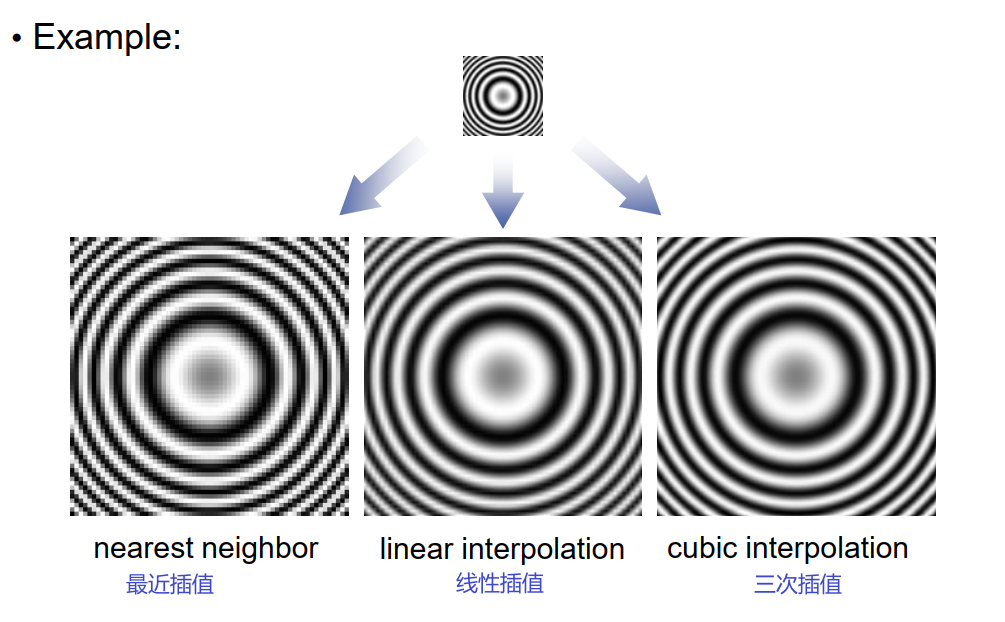
- 最近邻插值:nearest neighbor interpolation:
- 用阶跃函数逼近灰度函数
- 取最近整数位置的灰度值
- 问题:混叠 aliasing
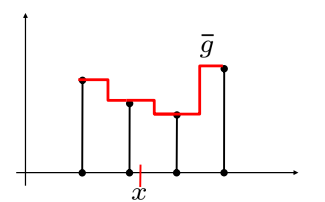

-
ID 中的线性插值
在 x 附近局部拟合线性函数
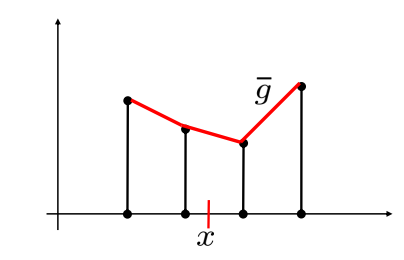
将线性插值扩展到二维:
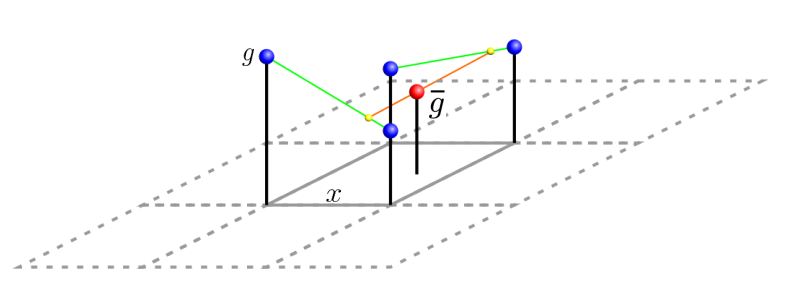
三次插值;三次内插
将三次多项式拟合到灰度等级
三次插值扩展到二维:
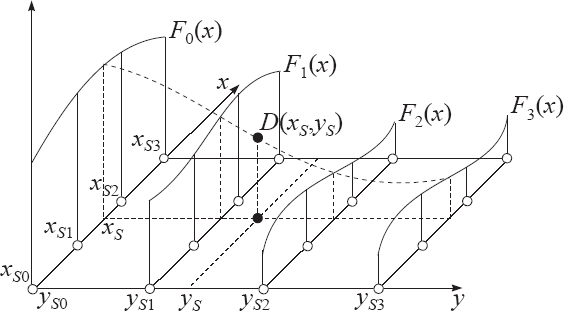
量化 Quantization
—– 将连续信号映射到离散值(自然数)
入射光: incident light:
\[I: \mathbb{R}^{2} \rightarrow \mathbb{R}\]数码相机信号:
\[g: \{0, \ldots, w-1\} \times\{0, \ldots, h-1\} \rightarrow\left\{0, \ldots, g_{\max }\right\} \\ w, h : image width, height\]需要从实值光强度转换为离散数字信号(模数转换器)need transformation from real valued light intensity to discrete digital signals (analog-to-digital converter)
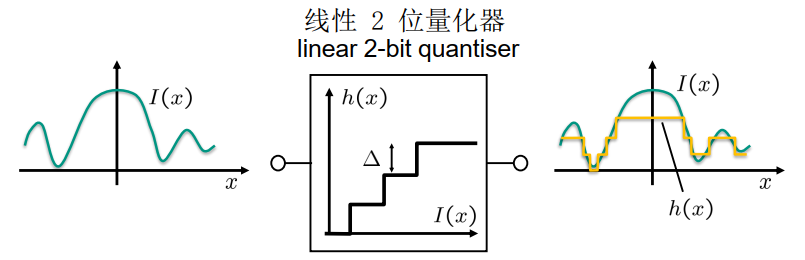
具有等距步长(“线性”)大小$\Delta$的特征
\[\begin{aligned} &g(x)=\max \left\{0, \min \left\{g_{\max },\left[\frac{I(x)}{\Delta}+\frac{1}{2}\right\rfloor\right\}\right\} \\ &h(x)=\Delta g(x) \end{aligned}\]非过载量化器的误差: error of non-overdriven quantiser:
\[I(x)-h(x) \in\left[-\frac{\Delta}{2}, \frac{\Delta}{2}\right]\]-
数码相机的特点: characteristic of digital cameras: 线性, 对数关系 linear ,logarithmic
在实际的摄像机记录拍摄数据的过程中通常会使用这两种记录方式:linear,log。简单的来说,linear会把亮度信息原原本本的记录下来,log则会对原本的亮度信息进行压缩以尽可能的节约存储空间,这个映射关系可以参考log曲线。这也是为什么大部分的linear记录方式下位深是16bit,而log的记录方式下位深只需要12bit或者10bit。log记录方式记录的拍摄素材因为对高光部分做了压缩,中间调部分提升很大,所以我们观看的时候会觉得很灰。


灰度截止值 grey level cutoff value
- 1 (binary images, “bitmaps”) → 1 bit/pixel
- 255 → 8 bit/pixel = 1 byte/pixel
- 4095 → 12 bit/pixel = 1.5 byte/pixel
- 65535 → 16 bit/pixel = 2 byte/pixel
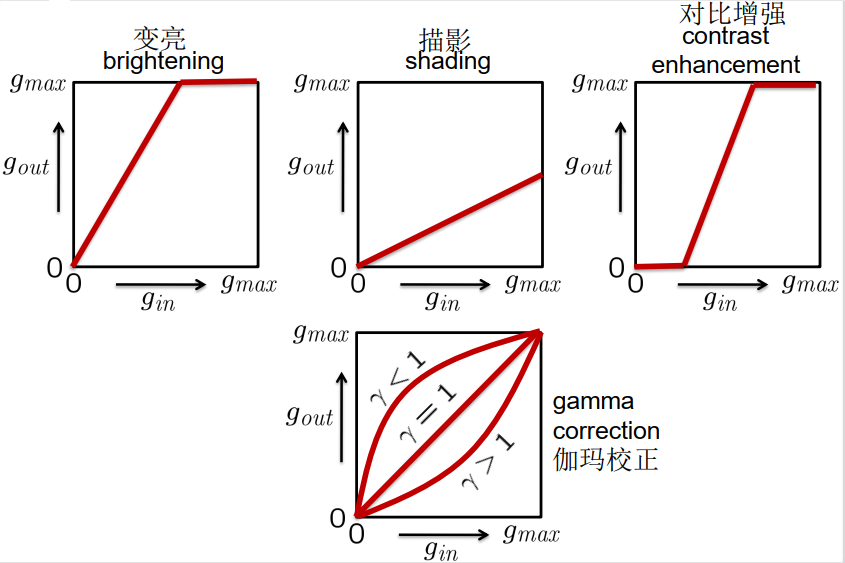
灰度分布校正 correction of grey level distribution
- 图像太暗/太亮 image too dark/too bright
- 低对比度 low contrast
- 非线性相机特性non-linear camera characteristic

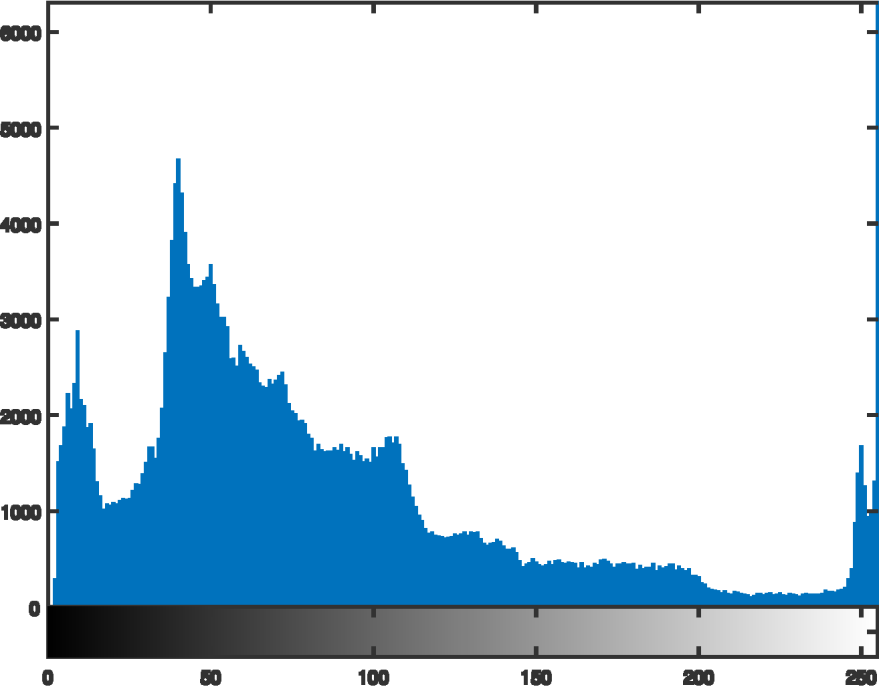
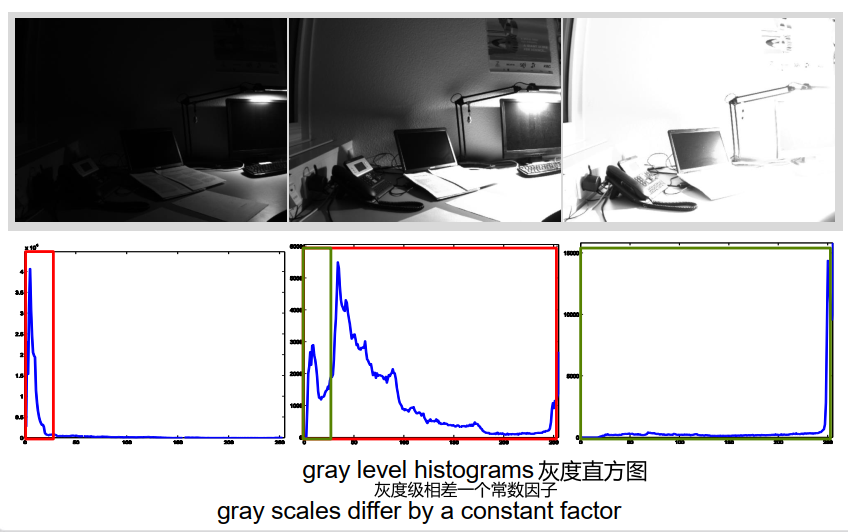
灰度直方图显示灰度分布

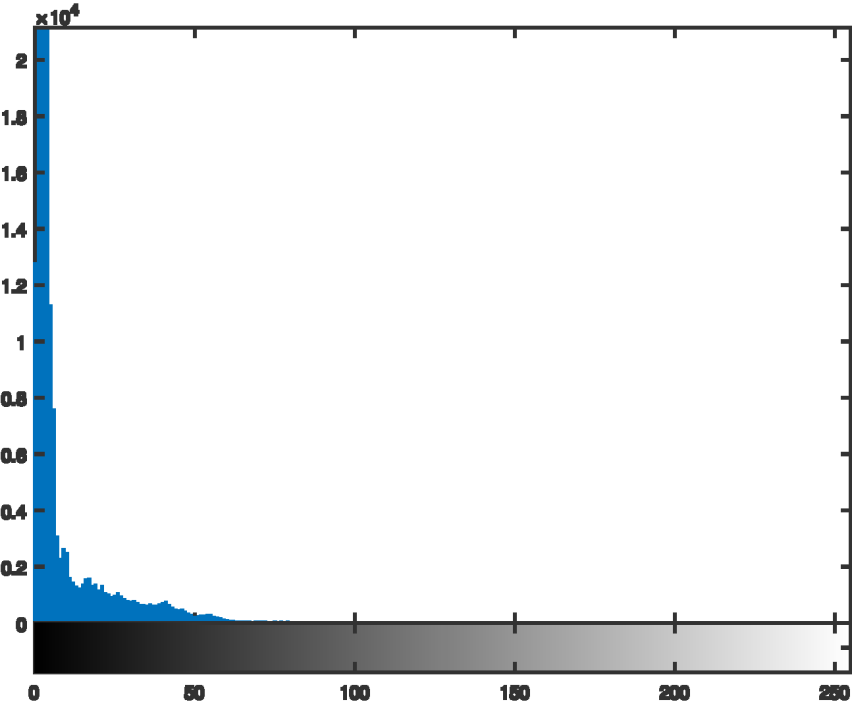
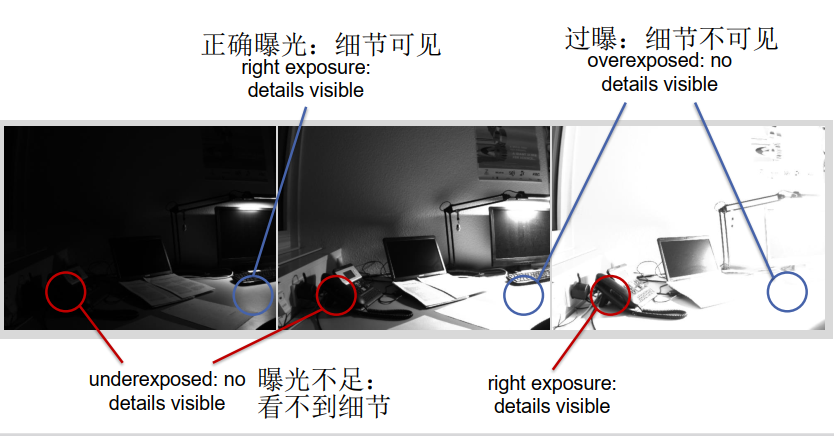
曝光不足的图像: • 打开相机的光圈 • 增加相机的曝光时间 • 增加增益 • 添加额外的光源 • 将灰度值乘以一个常数 • 在许多数码相机中实现的自动曝光
Underexposed images: • open aperture of camera • increase exposure time of camera • increase gain • add additional light sources • multiply grey values by a constant • auto-exposure implemented in many digital cameras

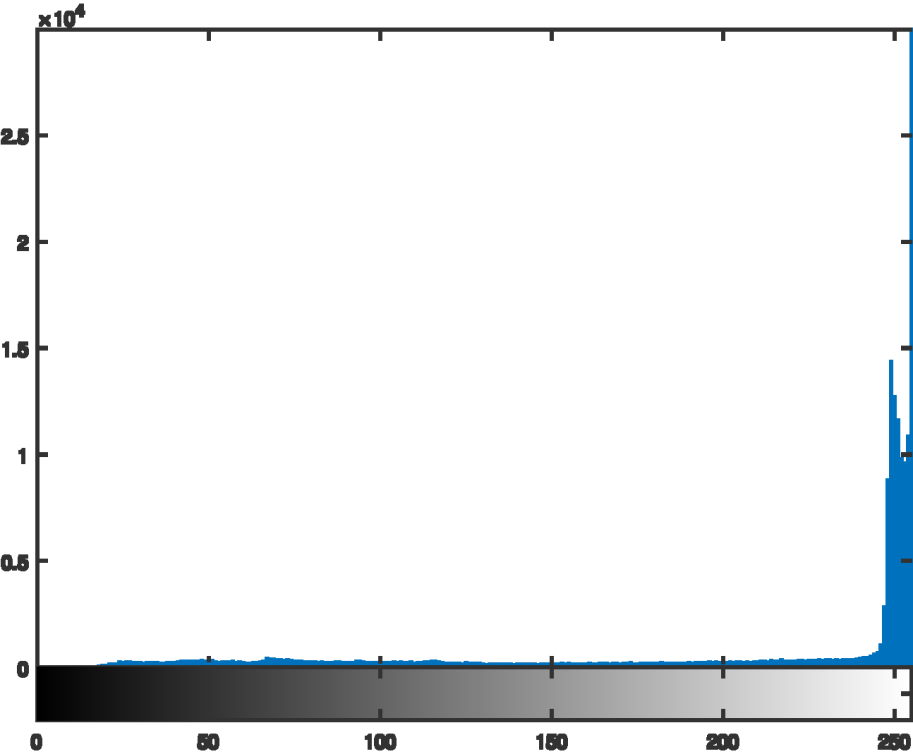
过度曝光的图像: • 由于截止值导致信息丢失,无法重建 • 相机光圈关闭 • 减少相机曝光时间 • 自动曝光 Overexposed images: • information loss due to cutoff value, no reconstruction possible • close aperture of camera • reduce exposure time of camera • auto-exposure



伽玛校正:Gamma correction:
\[g_{o u t}=g_{\max }\left(\frac{g_{i n}}{g_{\max }}\right)^{\gamma}\]伽马矫正 • 黑白度不变 • 非线性变换
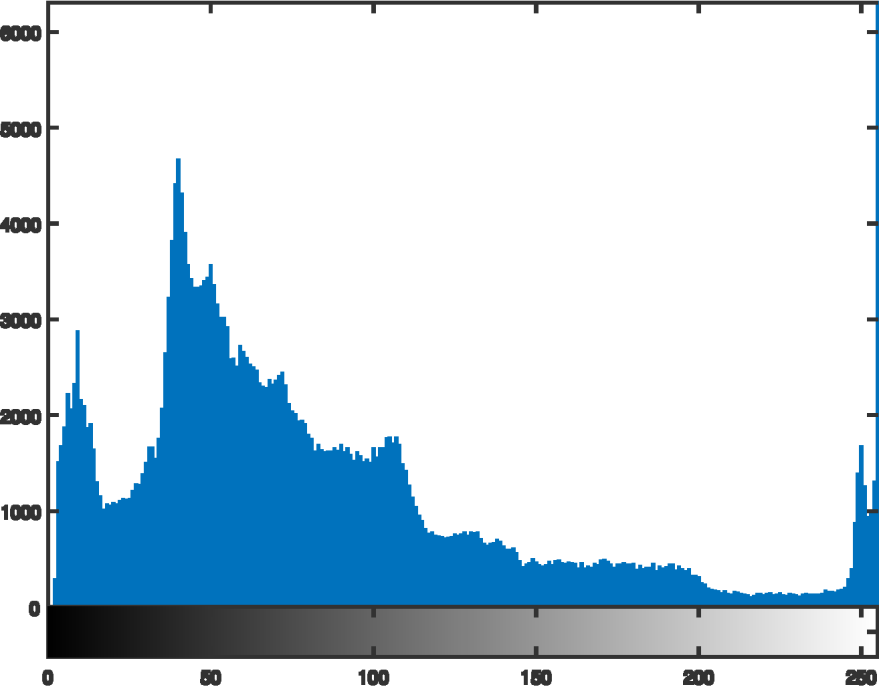
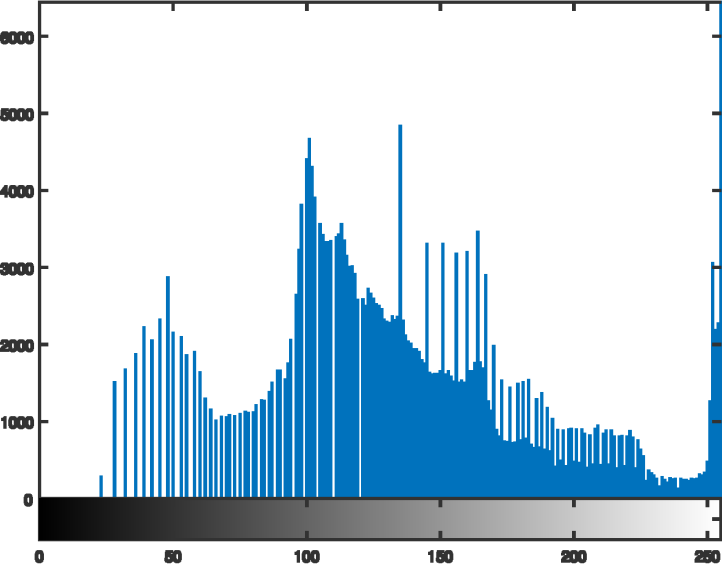
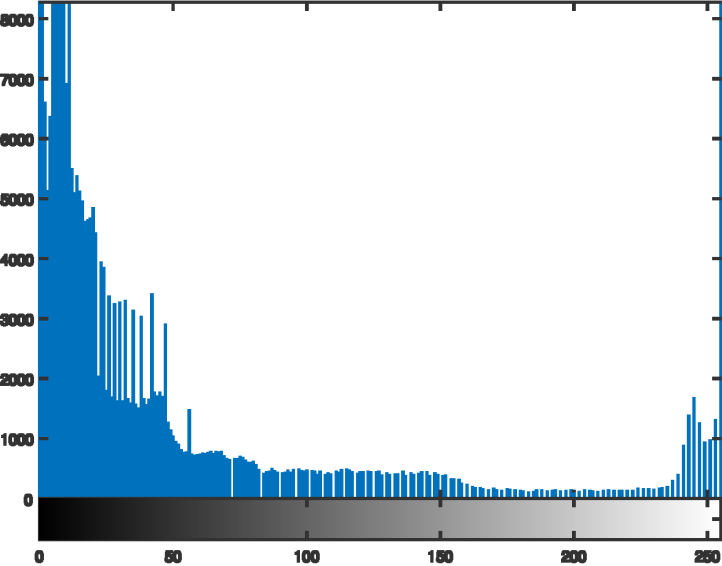
灰度变换 Grey Level Transformations
曝光序列 Exposure Series
包围曝光、高动态范围成像 (HDRI):结合曝光过度和曝光不足的图像提高灰度值分辨率

模糊和噪点Blur and Noise
卷积运算
卷积运算符
- – 采用两个函数
- – 创建一个新函数
- – 由逐点定义
我们分析:
$g$ is a 灰度图 gray level image
$f$ is a 是一个滤波函数 filter function
$h$ is a滤完了的图像 filtered image
卷积实现了一个线性滤波器convolution implements a linear filter
性质:
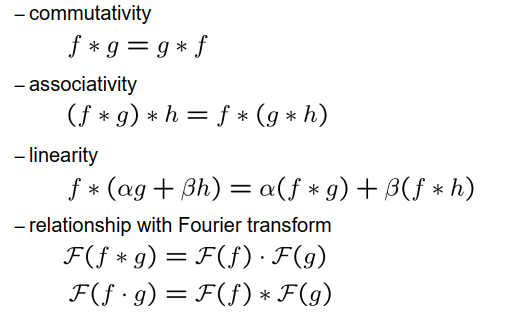
扩展到二维和离散情况:
\[\begin{aligned} &f, g: \mathbb{R}^{2} \rightarrow \mathbb{R} \\ &(g * f)(x, y)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(\tau, \rho) g(x-\tau, y-\rho) d \tau d \rho \end{aligned}\]对于我们只能在整数位评估的函数的情况
\[\begin{aligned} &f, g: \mathbb{Z} \rightarrow \mathbb{R} \\ &(g * f)(u)=\sum_{k=-\infty}^{\infty} f(k) g(u-k) \\ &f, g: \mathbb{Z}^{2} \rightarrow \mathbb{R} \\ &(g * f)(u, v)=\sum_{k=-\infty}^{\infty} \sum_{l=-\infty}^{\infty} f(k, l) g(u-k, v-l) \end{aligned}\]对图像卷积:

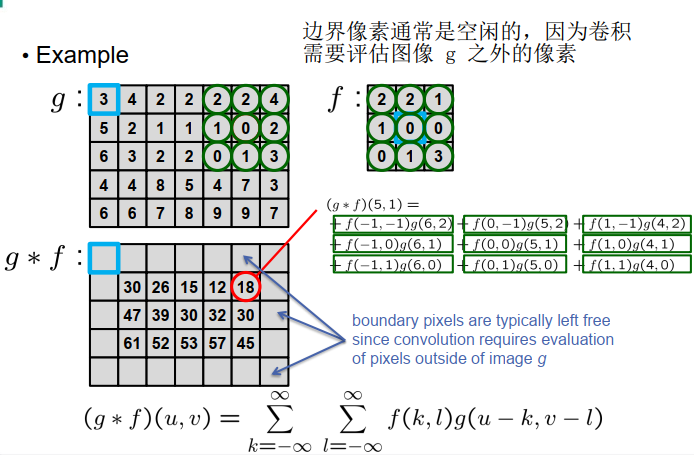
模糊和噪声的类型
- 运动模糊 motion blur
- 散焦像差 defocus aberration
- 传感器单元和放大器的统计噪声 statistical noise of sensor cells and amplifiers
- 故障传感器单元 malfunctioning sensor cells



模糊模型
-
运动模糊Motion blur:
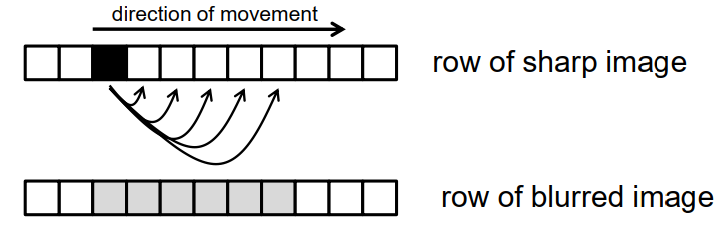
-
Gaussian blur:
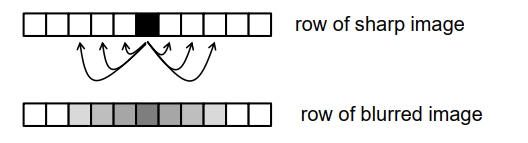
模糊可以用卷积建模 blur can be modeled with convolution
\[g_{\text {blurred }}=g_{\text {sharp }} * p\]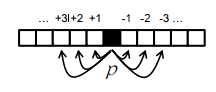
p = “点扩散函数”模型模糊 “point-spread-function” models blur
- 运动模糊(沿 x 轴 n 像素): motion blur (along x-axis by n pixels):
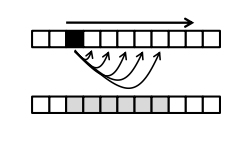
- 高斯模糊(方差 $\delta^2$):Gaussian blur (with variance $\delta^2$):
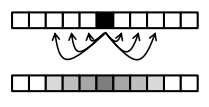
Wiener反卷积 Wiener Deconvolution
基于维纳滤波器从模糊图像中获取清晰图像的技术 techniques to obtain sharp image from blurred image based on Wiener filter
Wiener反卷积是一种常用的非盲线性图像恢复算法。
非盲:盲反卷积指事先不知道模糊核或PSF,非盲指事先知道模糊核或PSF
线性: 假设一个系统 $y=h * x+n$ ,其中 $y$ 是模糊图像, $x$ 是清晰图像, $h$ 是模糊 核, $n$ 是噪声。(PS: $n$ 与 $x$ 相互独立) 我们可以使用一个wiener卷积核 $g$ 使得
$x = g * y$
\[\begin{aligned} g_{b l u r r e d}=& g_{\text {sharp }} * p+v \\ & p: \text { point-spread-function } \\ & v: \text { pixel noise } \\ & \text { assume } g_{s h a r p} \text { and } v \text { be independent } \\ g_{\text {restored }}=& f * g_{b l u r r e d} \end{aligned}\]找到最小化的最优 f:
\[e(k)=\mathbb{E}\left[\left|\hat{g}_{\text {sharp }}(k)-\hat{g}_{\text {restored }}(k)\right|^{2}\right]\]$(\hat{g}$ denotes Fourier transform of $g$ ) (E denotes expectation value期望值)


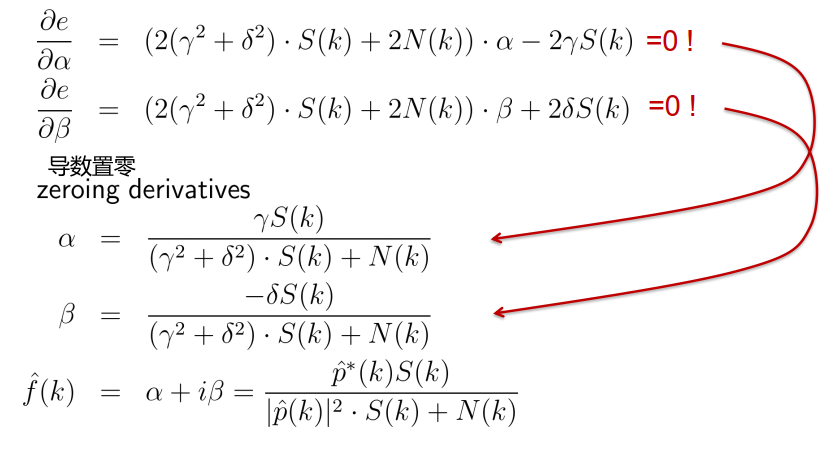
将 e 的导数归零以获得最小域: zeroing the derivative of e to obtain the minimum yields:
\[\widehat{f}(k)=\frac{\widehat{p}^{*}(k) S(k)}{\widehat{p}(k) \hat{p}^{*}(k) S(k)+N(k)}=\frac{\hat{p}^{*}(k)}{|\widehat{p}(k)|^{2}+\left(\frac{S(k)}{N(k)}\right)^{-1}}\]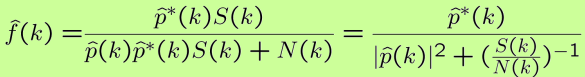
它定义了最优线性滤波器(维纳滤波器)
\[\frac{S(k)}{N(k)}\]是信噪比 is the signal-to-noise ratio
在无噪音情况下: in the noiseless case:
\[\widehat{f}(k)=\frac{1}{\widehat{p}(k)} \quad(\text { if } N(k)=0)\]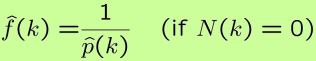
但是
$\frac{S(k)}{N(k)}$ 和 $\widehat{p}(k)$
必须知道


噪声模型 Models of Noise
- 随机干扰 杂乱噪声 statistical noise
- \[\begin{aligned} g_{\text {noisy }}(x, y) &=g_{s h a r p}(x, y)+v(x, y) \\ v(x, y) & \sim N\left(0, \sigma^{2}\right) i . i . d . \end{aligned}\]

- 传感器故障:malfunctioning sensors:
- \[g_{\text {noisy }}(x, y)= \begin{cases}g_{s h a r p}(x, y) & \text { with probability } p \\ \text { arbitrary任意的 } & \text { otherwise }\end{cases}\]

一、随机干扰:
基本思想:平均(平滑)
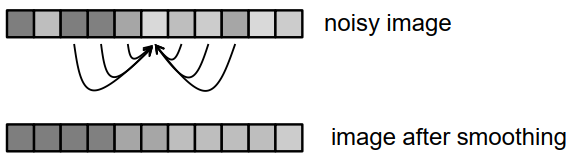
在同质区域效果很好,但在灰度边缘失败
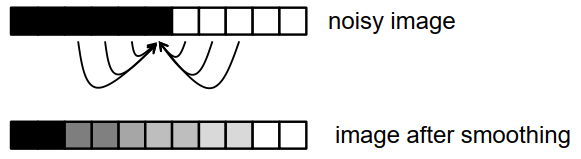
平滑滤波器
矩形滤波器 rectangular filter
\[f(x)= \begin{cases}\frac{1}{a} & \text { if }|x|<\frac{a}{2} \\ 0 & \text { otherwise }\end{cases}\]$\alpha$参数越大,平滑越强
高斯滤波Gaussian filter
\[f(x)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{1}{2} \frac{x^{2}}{\sigma^{2}}}\]$\delta$参数越大,平滑越强
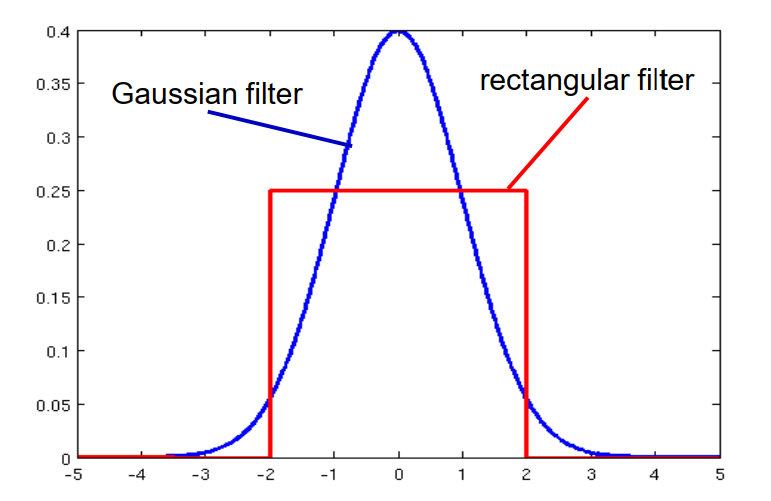
平滑滤波器的傅里叶变换
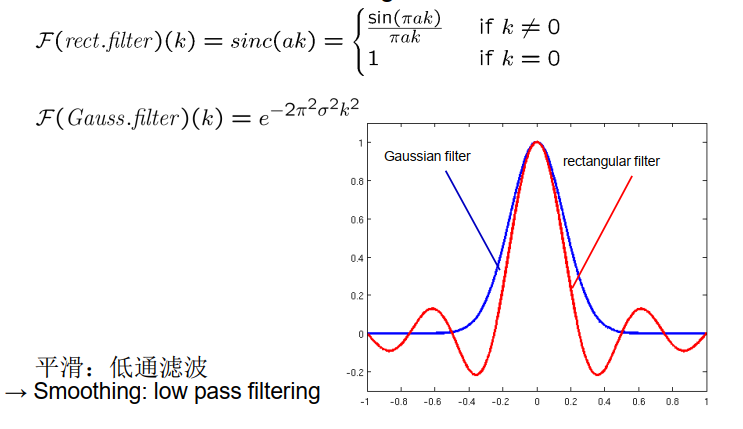
图像平滑滤波
掩模mask用选定的图像、图形或物体,对处理的图像(全部或局部)进行遮挡,来控制图像处理的区域或处理过程。用于覆盖的特定图像或物体称为掩模或模板。光学图像处理中,掩模可以是胶片、滤光片等。数字图像处理中,掩模为二维矩阵数组,有时也用多值图像。
矩形滤波器掩模:rectangular filter masks:
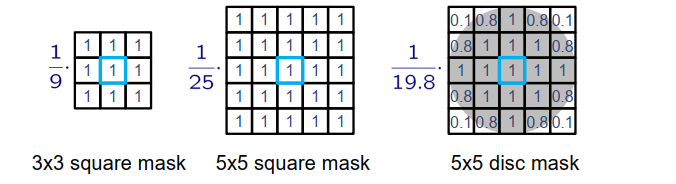
离散卷积 Discrete Convolution
高斯滤波器掩模 Gaussian filter masks:
高斯滤波器是一类根据高斯函数的形状来选择权值的线性平滑滤波器。
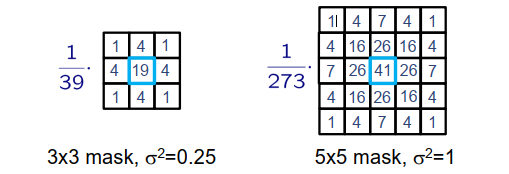
二项式滤波掩模 binomial filter masks
Binomial Filter是由牛津大学的Matthew Aubury(马修奥伯里)和英国皇家工程院的Wayne Luk(陆永青)在1994年提出的,提出的目的是为解决高斯滤波器在一组相互冲突的约束下选择滤波器系数的问题。他们提出了一种基于二项式系数的高斯逼近算法,该算法具有简单、准确和灵活的结构。另外一个优点就是二项式滤波器不需要多次运算,因此允许大型的滤波器结构在当前变成硬件中实现,比如现场可编程门阵列(FPGA)。此外,他的规则结构便于在定制VLSI中实现,并且可以转换生成高性能的收缩版本。
对于图像处理来说,常用二维零均值离散高斯函数作平滑滤波器。
高斯二项式系数计算一个有限维向量空间的子空间数。令q表示一个有限域里的元素数目,则在q元有限域上n维向量空间的k维子空间数等于$\left(\begin{array}{l}n \ k\end{array}\right)_q$
例子:
\[\begin{aligned} &\left(\begin{array}{l} 0 \\ 0 \end{array}\right)_{q}=\left(\begin{array}{l} 1 \\ 0 \end{array}\right)_{q}=1 \\ &\left(\begin{array}{l} 1 \\ 1 \end{array}\right)_{q}=\frac{1-q}{1-q}=1 \\ &\left(\begin{array}{l} 2 \\ 1 \end{array}\right)_{q}=\frac{1-q^{2}}{1-q}=1+q \\ &\left(\begin{array}{l} 3 \\ 1 \end{array}\right)_{q}=\frac{1-q^{3}}{1-q}=1+q+q^{2} \\ &\left(\begin{array}{l} 3 \\ 2 \end{array}\right)_{q}=\frac{\left(1-q^{3}\right)\left(1-q^{2}\right)}{(1-q)\left(1-q^{2}\right)}=1+q+q^{2} \\ &\left(\begin{array}{l} 4 \\ 2 \end{array}\right)_{q}=\frac{\left(1-q^{4}\right)\left(1-q^{3}\right)}{(1-q)\left(1-q^{2}\right)}=\left(1+q^{2}\right)\left(1+q+q^{2}\right)=1+q+2 q^{2}+q^{3}+q^{4} \end{aligned}\]和普通二项式系数一样,高斯二项式系数是中心对称的:
\[\left(\begin{array}{c} m \\ r \end{array}\right)_{q}=\left(\begin{array}{c} m \\ m-r \end{array}\right)_{q}\]特别地,
\[\begin{aligned} &\left(\begin{array}{c} m \\ 0 \end{array}\right)_{q}=\left(\begin{array}{c} m \\ m \end{array}\right)_{q}=1 \\ &\left(\begin{array}{c} m \\ 1 \end{array}\right)_{q}=\left(\begin{array}{c} m \\ m-1 \end{array}\right)_{q}=\frac{1-q^{m}}{1-q}=1+q+\cdots+q^{m-1} \quad m \geq 1 \end{aligned}\]当 $q=1$ 时,有
\[\left(\begin{array}{c} m \\ r \end{array}\right)_{1}=\left(\begin{array}{c} m \\ r \end{array}\right)\]- 使用二项式系数$\left(\begin{array}{l}n \ k\end{array}\right)$的二项式滤波器掩码对高斯masks的逼近

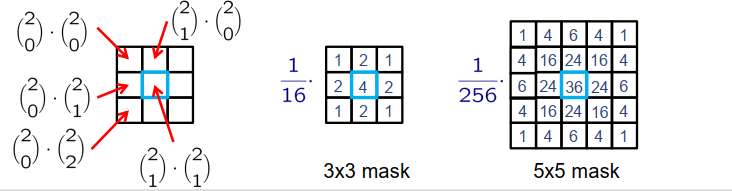

双边滤波 Bilateral filter
双边滤波(Bilateral filter)是一种非线性的滤波方法,是结合图像的空间邻近度和像素值相似度的一种折衷处理,同时考虑空域信息和灰度相似性,达到保边去噪的目的。具有简单、非迭代、局部的特点。
高斯滤波去降噪,会较明显地模糊边缘,对于高频细节的保护效果并不明显。

我们知道,对图像进行空间域滤波的方法是使用一个结构元素(核)来对原图像进行卷积。而这个结构元素就会对原图像进行卷积操作,从而得到一个新的图像,即输出图像。我们知道,这个结构元素是不会变的。但是!但是!但是!在双边滤波算法中就不是如此了。为了使图像的边缘得到保留,就要根据当前被卷积像素的邻域进行观察,“推断”是否是边缘点和接近边缘的点。因此,结构元素就会改变,从而保留边缘点。下面的一组图中,图a是原图像,图c是输出。而中间的图像是什么呢?显然,这是原图中根据某个点的邻域生成的,专属于这个点的结构元素。
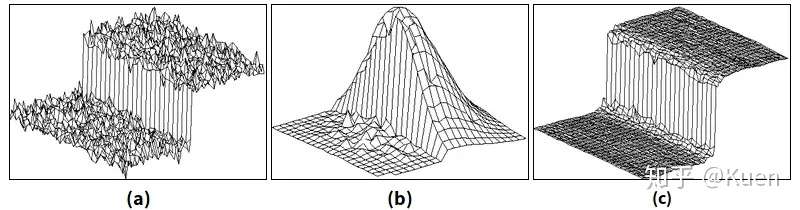
可以看到,原图中显然有一个灰度的突变,这就表示是边缘。灰度值高的地方不应该和灰度低的区域进行混合,所以,图像中接近边缘的一个点就会生成图b这样的结构元素。那么这个接近边缘的点在哪里呢?大概就在标出的这个区域。
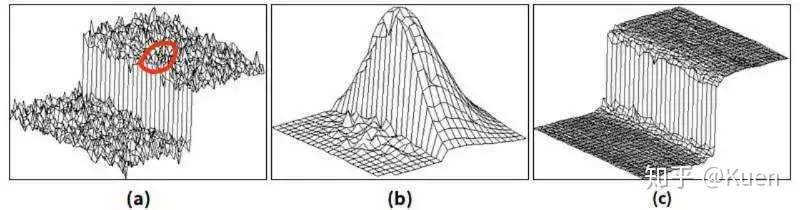
而生成这样的结构元素的方法,是将我们原本的高斯核,与一个能“推断”出是否在边缘点的结构元素相乘,如下图中间的结构元素。

下图是双边滤波的原理示意图:
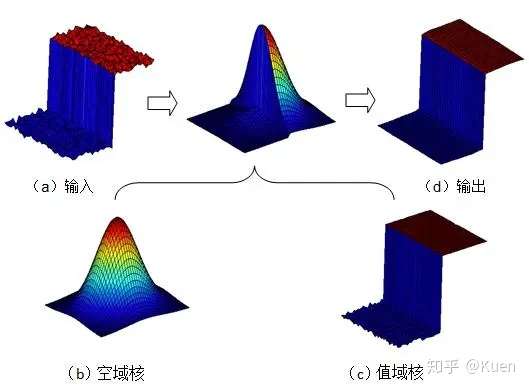
双边滤波器的输出像素依赖于当前被卷积像素的邻域。 $i$ 和 $j$ 是当前被卷积像素的坐标点, $k$ 和 $l$ 是邻域像素的坐标点:
\[r(i, j, k, l)=\exp \left(-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right)\]可以看到,它 取决于被卷积像素的灰度值和邻域像素的灰度值的差。我们知道,边缘会有较大的 灰度变化,而这个公式就会使边缘和边缘另一边的区域生成比较小的权值,与被卷积像素的灰度值 类似的区域会生成比较大的权值,就像之前图中的一个 “断崖”。
相乘就得到加权系数 $w$ :
\[w(i, j, k, l)=\exp \left(-\frac{(i-k)^{2}+(j-l)^{2}}{2 \sigma_{d}^{2}}-\frac{\|f(i, j)-f(k, l)\|^{2}}{2 \sigma_{r}^{2}}\right)\](注:分割线以内的内容来自知乎Jargon https://zhuanlan.zhihu.com/p/127023952,侵删)
椒盐噪声 Salt-and-Pepper Noise

中值滤波器 Median filter
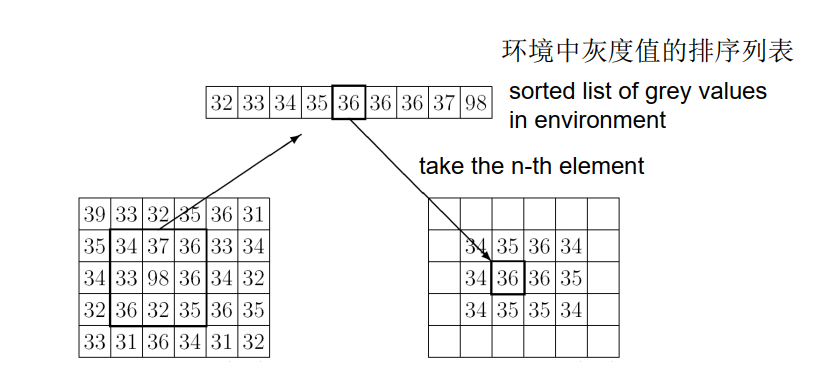
中值滤波器:
- 对参考像素周围环境中的灰度值进行排序
- 取排序列表中间的灰度值


